LeetCode 721.账户合并 题解
题目信息
LeetoCode地址: 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
题目理解
原题使用的是名称和账号的邮箱地址,好多字母,可能有些人会不太好理解。我换了一种场景:联想一下,诸如《魔兽世界》《地下城与勇士》这样的网络游戏,每个玩家都可以创建多个游戏角色,每个游戏角色的ID都是服务器唯一的。注意,玩家的姓名在现实生活中是完全可以重复的。
在下图上半部分里,有一些玩家: 两位周小董, 两位张小涵,他们都拥有一些游戏角色。
按照题目的意思,因为两个周小董都拥有角色《战斗至死》,所以这两个周小董其实同一个人,他们的游戏角色是可以直接合并,属于同一个人的。
相反的,因为两位张小涵的游戏角色都不重复,所以这是两位重名的玩家,他们的游戏角色是不应该合并的。
综上,如下图下半部分所示,最终周小董合并之后有三个游戏角色,而两位张小涵的游戏角色保持不变。
 图1
图1
由于玩家合并之后,一定没有两位玩家拥有相同的角色,所以可以得出结论,所有的角色ID都是独一无二的,而不像合并前有重复。
解题思路
数组并查集+哈希表
我们已经知道最终合并之后是不存在重复的角色ID的,找到它们并确定哪个游戏角色属于哪个玩家是很简单的,使用HashMap就可以做到。问题的关键在于如何找到相同玩家的不同角色ID,并将他们合并。
首先,我们先给所有第一次出现角色ID按照从0开始递增的方式编号. 可以看到,我们总共有0到5也就是6个不重复的角色ID.
 图2
图2
要合并它们,我们可以换个思考方式。那就是除了利用玩家名字之外,还有没有别的办法表示一批角色ID是属于同一个人的?实际是有的!我们可以使用每个玩家的第一个角色作为这一批角色的父亲,或者叫做根。如果用图表示,就类似下面这样:
 图3
图3
现在,让我们聚焦到根是《0.一往无前》和《3.逍遥自在》的这两个树状结构。
 图4
图4
显而易见的,它们都拥有相同的《1.战斗至死》这个角色ID。想要将他们合并,也就是让这两个树状结构拥有相同的根。由于我们是按照从左到右的顺序遍历的,所以左边这棵树合并到右边这棵树是最自然的结果。如何做?以《1.战斗至死》举例,我们让它的根的根,等于第二棵树的根的根。
很多人要迷惑了啊,什么根的根的根。一个一个来看。第一个根是上图左侧的《1.战斗至死》的根,也就是《0.一往无前》。第二个根是上图左侧的《0.一往无前》的根,是它自己。第三个根,也就是我们在便利第二个周小董的游戏角色时,遇到的重复元素《1.战斗至死》的根,也就是《3.逍遥自在》。至此,两棵树会合并完成了。
最终状态就是下图的状态。
 图4
图4
现在让我们看看剩下两棵树
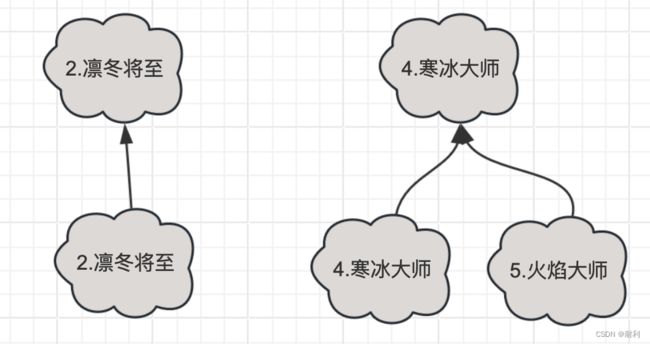 图5
图5
显而易见的,这两棵树都没有共同的角色ID,他们在合并操作和会保持原样。
那么创建这种类树结构并通过找根合并两棵树的结构是什么?就是大名鼎鼎的并查集。
public class UnionFind {
/**
* parent数组存储所有元素的父亲节点
*/
int[] parent;
/**
* 初始化并查集
* @param i 不重复元素的数量,在游戏角色的例子中,它的值是6
* 每一个元素的初始父亲节点都是它本身
*/
public UnionFind(int i) {
parent = new int[i];
IntStream.range(0, i).forEach(element -> parent[element] = element);
}
/**
* 只要父亲节点不是它自己,就不断递归寻找父亲节点的父亲节点,直到根节点
* @param i 需要寻找父亲的节点索引
* @return 根节点索引
*/
public int find(int i) {
if (parent[i] == i) {
return i;
}
return find(parent[i]);
}
/**
* 将i节点的根节点的父亲节点设置为j节点的根节点
* @param i 需要被合并的节点
* @param j 合并到的目的地节点
*/
public void union(int i, int j) {
parent[find(i)] = find(j);
}
}根据游戏角色这个例子的分析可以看到,使用并查集最关键的步骤如下:
- 找到所有集合的所有不重复元素,并从0递增编号
- 遍历所有集合,将属于同一个集合的所有元素进行union,根元素是这个集合的第一个元素。在这个过程结束后,合并操作就已完成。
- 遍历所有不重复元素,将同根的元素存放在合适的数据结构比如List中进行后续的包装。
在理解了上面这个模型后,将玩家换成题目里的account,游戏角色ID换成email,原题的解法就呼之欲出了。
public List> accountsMerge(List> accounts) {
int emailCount = 0;
//存储每个唯一的email到编号的映射,从0递增
HashMap emailMap = new HashMap<>();
//存储每个唯一的email到所属的account名称的映射
HashMap emailAccountNameMap = new HashMap<>();
//找到所有不重复的email
for (List account : accounts) {
for (int i = 1; i account : accounts) {
String firstEmail = account.get(1);
int firstEmailIndex = emailMap.get(firstEmail);
for (int i =2; i < account.size(); i++) {
String email = account.get(i);
Integer emailIndex = emailMap.get(email);
unionFind.union(emailIndex, firstEmailIndex);
}
}
//存储account的索引到所拥有的email集合的映射关系
Map> map = new HashMap<>();
//存储所有不重复email到同属account对应的List中
for (String email : emailMap.keySet()) {
int i = unionFind.find(emailMap.get(email));
List orDefault = map.getOrDefault(i, new ArrayList<>());
orDefault.add(email);
map.put(i, orDefault);
}
List> result = new ArrayList<>();
// 按照题目要求包装返回结果
for (List emails : map.values()) {
emails.sort(Comparator.naturalOrder());
ArrayList accountEmailList = new ArrayList<>();
accountEmailList.add(emailAccountNameMap.get(emails.get(0)));
accountEmailList.addAll(emails);
result.add(accountEmailList);
}
return result;
} 链表并查集
除了使用数组结果表示并查集以外,我们还可以通过链表的方式表达,甚至它在结构上更加的直观。如果将一个email当作并查集中的一个节点,它应该有这些属性:email名称,根节点,就是这么直观!在初始状态时,email的根节点是account,而account的根节点就是它本身。
回想一下数组实现的并查集,我们还需要一个find方法和union方法,前者让它返回当前节点的根节点,后者将两个集合进行合并。在使用链表实现时,会略微又些不同。为了能够高效的返回当前节点的根节点,我们要在find方法里一边查一遍修改根节点的指针值,而这个修改动作就是union的一部分。
链表并查集节点Node的具体实现如下:
class Node {
String name;
Node parent;
public Node(String name, Node parent) {
this.name = name;
if (parent == null) {
this.parent = this;
} else {
this.parent = parent;
}
}
public String getName() {
return name;
}
public Node find() {
if (this.parent == this) {
return this;
}
Node current = this.parent;
Node rootOfParent = current.find();
if (current != rootOfParent) {
current = rootOfParent;
current.find();
}
this.parent = current;
return current;
}
public void setParent(Node parent) {
this.parent = parent;
}
}很显然,如果我们只是一个个账户单独遍历的话,email节点的根节点永远都是它们所属的account,那我要怎么做账户之间的合并操作呢?我们说过,合并的触发关键是两个集合之间有相同的元素。当相同email出现时,有一步关键操作会将前一个包含该email集合的根节点的根节点修改为后一个email的根节点,也即是
emailNode.find().setParent(parentAccount);
之后,我们在通过节点的find方法将其老的根节点刷新成新的。具体代码示例如下
public List> accountsMerge(List> accounts) {
// email到其node的映射关系,注意,这里是没有保存account节点的,因为没有必要
// 我们可以通过调用email node的find方法轻松获得account节点
Map nodeMap = new HashMap<>();
for (List account : accounts) {
Node parentAccount = new Node(account.get(0), null);
for (int i = 1; i < account.size(); i++) {
String emailName = account.get(i);
//如果已经存在该emailName,说明之前的集合已经包含了它,需要进行union操作
if (nodeMap.containsKey(emailName)) {
Node emailNode = nodeMap.get(emailName);
// union操作的关键代码,将前一个集合的根节点的根节点设置为新的集合的根节点
// 这样做为后面使用node.find方法获得最终根节点做好最后铺垫
emailNode.find().setParent(parentAccount);
} else {
//如果不存在,那就创建新的节点,根节点就是当前账户名对应的节点
nodeMap.put(emailName, new Node(emailName, parentAccount));
}
}
}
Map> nodeListMap = new HashMap<>();
for (Node node : nodeMap.values()) {
// 这一步在获取最终根节点的同时,也刷新的node的根节点
Node parent = node.find();
if (nodeListMap.containsKey(parent)) {
//如果根节点已存在,那只管往后累加就好了
nodeListMap.get(parent).add(node.getName());
} else {
//如果不存在,则创建新的列表,先加账户名,再累加email
nodeListMap.put(parent, new ArrayList<>(Arrays.asList(parent.name, node.name)));
}
}
nodeListMap.values().forEach(it -> Collections.sort(it.subList(1, it.size())));
return new ArrayList<>(nodeListMap.values());
} 在账户数为n,账户内邮箱数为m的情况下:
时间复杂度: O(m*n),只有遍历账户和邮箱时最耗时,find操作本身是常数复杂度。
额外空间复杂度:O(m*n),用于存储nodeListMap。
DFS+BFS
其实我们分析了这多多,发现最关键的判断两个账号是否应该合并的依据还是两个集合有没有重复的元素。如果能够在遍历A账户的时候发现某个邮箱在B账户也出现了,触发了对B账户的遍历,而在遍历B账户的时候,发现另一个邮箱在C账户也出现了,又触发了对C账户的遍历。。。直到遍历完所有有关的账户。是不是递归的味道就出来了?那不就是DFS的主场么!
根据上面的描述,我们希望能够建立起任意一个邮箱到同账户其他邮箱的映射,但这样重复且笨重。更为简单高效的做法是,让同一账户的第一个邮箱建立起到其他所有邮箱的映射,而让其他邮箱建立起到第一个邮箱的映射。这样做后,任意一个邮箱,我都可以找到它的同账户第一个邮箱,然后再找第一个邮箱的同组其他邮箱,就是全集了。
这样做还有一个好处是,一旦某一个邮箱在两个账户中出现了,我们就拥有了该邮箱到两个账户首邮箱的映射,也就意味着能够轻松找到这两个首邮箱所在账户的所有邮箱。通过递归的方式,我们能够找到所有具有共同邮箱的账户,就像火烧连营一样,一条船着火,其他所有连接着的船都会着火。
下面是代码实现。在账户数为n,账户内邮箱数为m的情况下:
时间复杂度: O(m*n^2),最后在n个账户中进行bfs搜索,深度为n,每次搜索平均m次。
额外空间复杂度:O(m*n),用于存储graph。
public List> accountsMerge(List> accounts) {
//使用Map表示节点与哪些其他节点连通
Map> graph = new HashMap<>();
for (List account : accounts) {
//每一个account的第一个email都与account内其他的所有email连通
String firstEmail = account.get(1);
List firstEmailList = graph.getOrDefault(firstEmail, new ArrayList<>());
for (int i = 2; i emailList = graph.getOrDefault(email, new ArrayList<>());
emailList.add(firstEmail);
graph.put(email, emailList);
}
graph.put(firstEmail, firstEmailList);
}
List> result = new ArrayList<>();
//visited是用来保证不会重复遍历的关键组件,如果不加上,会导致循环遍历最终栈溢出
HashSet visited = new HashSet<>();
for (List account : accounts) {
String firstEmail = account.get(1);
List emailList = new ArrayList<>();
//通过bfs遍历该account下所有的email,如果某个email在其他account里出现,则bfs还会遍历其他account的email,
//因为这个email同时连通了两个account的第一个email,且该email又连通了两个account的所有email
bfs(firstEmail, visited, emailList, graph);
if (!emailList.isEmpty()) {
emailList.sort(Comparator.naturalOrder());
List accountEmailList = new ArrayList<>();
accountEmailList.add(account.get(0));
accountEmailList.addAll(emailList);
result.add(accountEmailList);
}
}
return result;
}
private void bfs(String firstEmail, HashSet visited, List emailList, Map> graph) {
//如果visited包含某个account的第一个email,则说明这个email的所有其他连通email都已经遍历过,直接返回即可
if (visited.contains(firstEmail)) {
return;
}
emailList.add(firstEmail);
visited.add(firstEmail);
//遍历所有firstEmail连通的其他email
for (String email : graph.get(firstEmail)) {
bfs(email, visited, emailList, graph);
}
}