机器学习周报第23周

摘要

在深度学习中，卷积神经网络（CNN）是一种被广泛应用于图像处理和其他领域的神经网络架构。卷积层、池化层以及适当的填充和步长设置是构建有效的CNN模型的关键组成部分。本文将讨论这些概念，特别是涉及到填充、卷积步长和池化层的影响。 在卷积操作中，填充是在输入数据周围添加额外的值，以便保持特征图的大小。填充有助于防止特征图尺寸的过度减小，确保在卷积过程中保留输入图像的边缘信息。适当的填充可以改善模型的性能，特别是在网络的边缘部分。 步长定义了卷积核在输入上滑动的步长。较大的步长会导致输出特征图的尺寸减小，减小计算负担。然而，较小的步长可以保留更多的细节信息。选择适当的步长取决于问题的复杂性和计算资源的可用性。 池化层通过降采样的方式减小特征图的维度，减少计算负担，并提高模型的计算效率。常见的池化操作包括最大池化和平均池化，用于保留输入区域的最显著特征。池化有助于提取更显著的特征，同时增加模型的平移不变性。

Abstract

In deep learning, convolutional neural network (CNN) is a neural network architecture that is widely used in image processing and other fields. Convolutional layers, pooling layers, and appropriate padding and step size settings are key components in building effective CNN models. In this paper, we will discuss these concepts, particularly as they relate to the effects of padding, convolutional step size, and pooling layers. In a convolution operation, padding is the addition of extra values around the input data in order to maintain the size of the feature map. Padding helps to prevent excessive reduction in the feature map size and ensures that the edge information of the input image is preserved during the convolution process. Proper padding can improve the performance of the model, especially in the edge portion of the network. The step size defines the length of the step at which the convolution kernel slides over the input. A larger step size results in a smaller size of the output feature map, reducing the computational burden. However, a smaller step size preserves more detailed information. Choosing the appropriate step size depends on the complexity of the problem and the availability of computational resources. The pooling layer reduces the dimension of the feature map by downsampling, reducing the computational burden and improving the computational efficiency of the model. Common pooling operations include maximum pooling and average pooling for retaining the most significant features in the input region. Pooling helps to extract more significant features while increasing the translation invariance of the model.

一、卷积神经网络

1.1 padding

如果你用一个3×3的过滤器卷积一个6×6的图像，你最后会得到一个4×4的输出，也就是一个4×4矩阵。这背后的数学解释是，如果我们有一个n×n的图像，用f×f的过滤器做卷积，那么输出的维度就是(n - f + 1) × (n - f + 1)。在这个例子里是6-3+1=4。

这样的话会有两个缺点，第一个缺点是每次做卷积操作，你的图像就会缩小。第二个缺点是那些在角落或者边缘区域的像素点在输出中采用较少，意味着你丢掉了图像边缘位置的许多信息。为了解决这两个问题，一是输出缩小，二是图像边缘的大部分信息都丢失了，你可以在卷积操作之前填充这幅图像。在这个案例中，你可以沿着图像边缘再填充一层像素。如果你这样操作了，那么6×6的图像就被你填充成了一个8×8的图像。如果你用3×3的图像对这个8×8的图像卷积，你得到的输出就不是4×4的，而是6×6的图像，就得到了一个尺寸和原始图像6×6的图像。习惯上，你可以用0填充，如果p表示填充的数量，在这个例子中，p=1，因为在周围都填充了一个像素点。输出维度变成了（一般向下取整）,
这样一来，丢失信息或者更准确来说角落或图像边缘的信息发挥的作用较小的这一缺点就被削弱了。

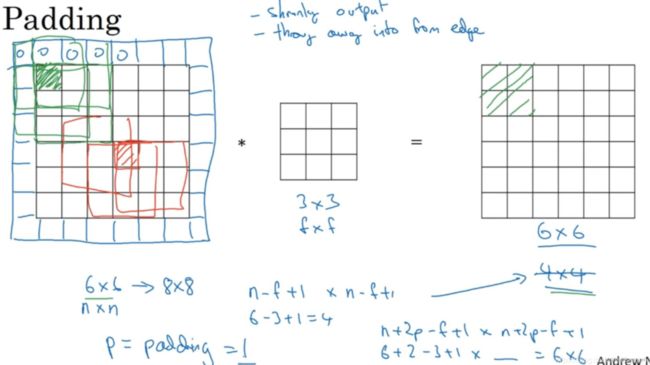
如果你想的话，也可以填充两个像素点。至于选择填充多少像素，通常有两个选择，分别叫做Valid卷积和Same卷积。

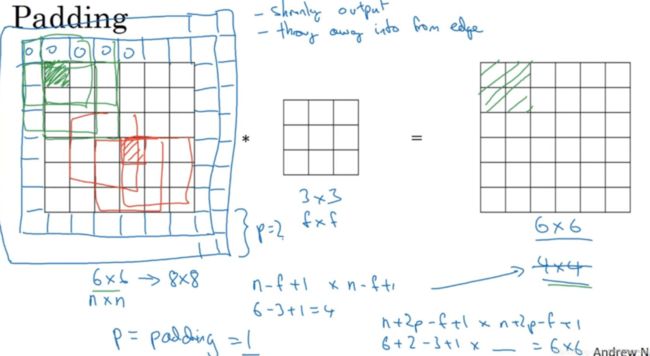
Valid卷积意味着不填充。另一个经常被用到的填充方法叫做Same卷积，那意味你填充后，你的输出大小和输入大小是一样的。利用n+2p-f+1=n求解，使得输出和输入大小相等，那么p = (f - 1)/2。

习惯上，计算机视觉中，f通常是奇数，甚至可能都是这样。你很少看到一个偶数的过滤器在计算机视觉里使用，Andrew认为有两个原因。

其中一个可能是，如果f是一个偶数，那么你只能使用一些不对称填充（asymmetric padding）。只有是奇数的情况下，Same卷积才会有自然的填充，我们可以以同样的数量填充四周，而不是左边填充多一点，右边填充少一点，这样不对称的填充。

第二个原因是当你有一个奇数维过滤器（odd dimension filter），比如3×3或者5×5的，它就有一个中心点（central position）。有时在计算机视觉里，如果有一个中心像素点（central pixel）会更方便，便于指出过滤器的位置。习惯上，Andrew推荐你只使用奇数的过滤器。

总之，你已经看到如何使用padding卷积，为了指定卷积操作中的padding，你可以指定p的值。也可以使用Valid卷积，也就是p=0。也可使用Same卷积填充像素，使你的输出和输入大小相同。以上就是padding，在接下来的视频中我们讨论如何在卷积中设置步长。

1.2 卷积步长

如果你想用3×3的过滤器卷积这个7×7的图像，和之前不同的是，我们把步幅设置成了2。注意一下左上角，这个点移动到其后两格的点，跳过了一个位置。然后你还是将每个元素相乘并求和，你将会得到的结果是100。依次类推，得到最终结果。如果你使用一个f x f的过滤器卷积一个n x n的图像，padding为p，步幅为s，在这个例子中，n = 7，p = 0， f = 3，s = 2，(7 + 0 - 3)/2 + 1 = 3，即3×3的输出。

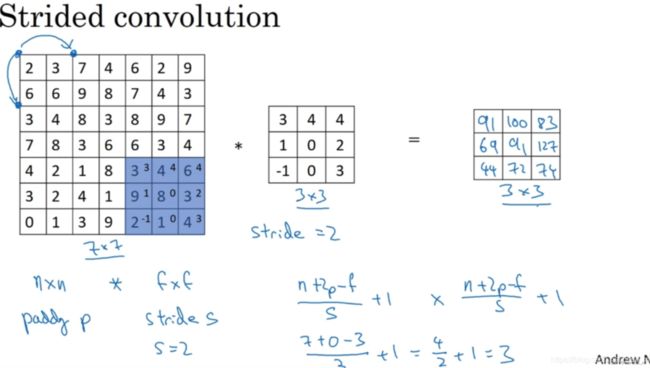
注意一个细节，如果商（fraction）不是一个整数（integer），则向下取整。这个原则实现的方式是，你只在蓝框完全包括在图像或填充完的图像内部时，才对它进行运算。如果有任意一个蓝框移动到了外面，那就不要进行相乘操作，这是一个惯例（convention）。3×3的过滤器必须完全处于图像中或者填充之后的图像区域内才输出相应结果。

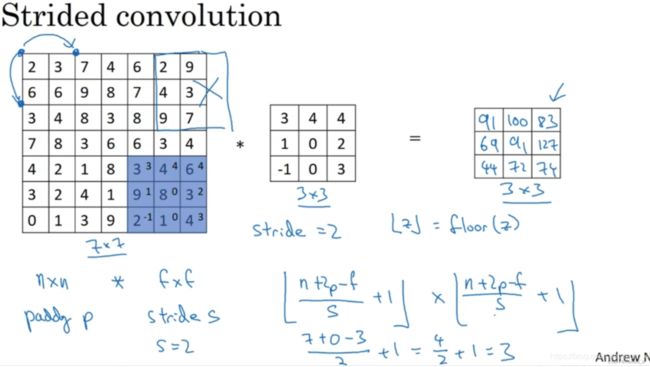
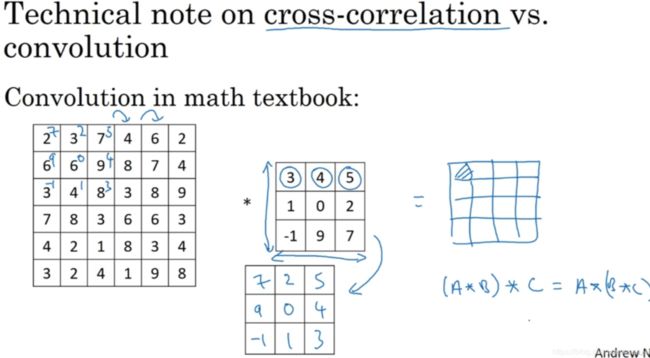
（这一部分了解即可）如上图，这里有一个关于互相关（cross-correlation）和卷积（convolution）的技术性建议（technical comment）。这不会影响到你构建卷积神经网络的方式，但取决于你读的是数学教材（math textbook）还是信号处理教材（signal processing textbook）。在数学教材中，卷积首先将3 x 3的过滤器沿水平和垂直轴翻转，然后再用这个翻转的矩阵进行元素乘积求和，而我们在视频中定义卷积运算时，跳过了这个镜像操作（mirroring operation）。从技术上讲，我们在前面视频中使用的操作，有时被称为互相关（cross-correlation）而不是卷积（convolution）。但在深度学习文献中，按照惯例，我们将（不进行翻转操作）叫做卷积操作。因此我们将在这些视频中使用这个约定。如果你读了很多机器学习文献的话，你会发现许多人都把它叫做卷积运算，不需要用到这些翻转。

事实证明在信号处理中或某些数学分支中，在卷积的定义包含翻转，使得卷积运算符拥有这个性质（enjoy this property），即结合律（associativity）：
这一性质对深度神经网络来说并不重要，因此省略了这个双重镜像操作（omitting this double mirroring operation），既简化了代码，又使神经网络也能正常工作。

现在已经了解了如何进行卷积，以及如何使用填充，如何在卷积中选择步幅。但到目前为止，我们所使用的是关于矩阵的卷积。在下一集视频中，将看到如何对立体进行卷积，这将会使你的卷积变得更加强大。

1.3 单层卷积网络

我们知道如何通过两个过滤器卷积处理一个三维图像，并输出两个不同的4×4矩阵。假设使用第一个过滤器进行卷积，得到第一个4×4矩阵，形成一个卷积神经网络层，然后增加偏差（bias），它是一个实数（real number），通过Python的广播机制给这16个元素都加上同一偏差。然后应用非线性函数，它是一个非线性激活函数ReLU，输出结果是一个4×4矩阵。

对于第二个4×4矩阵，我们加上不同的偏差，它也是一个实数，16个数字都加上同一个实数，然后应用非线性函数，也就是一个非线性激活函数ReLU，最终得到另一个4×4矩阵。重复我们之前的步骤，把这两个矩阵堆叠起来，最终得到一个4×4×2的矩阵。我们通过计算，从6×6×3的输入推导出一个4×4×2矩阵，它是卷积神经网络的一层，把它映射到标准神经网络中四个卷积层中的某一层或者一个非卷积神经网络中。

注意向前传播的一个操作是：这里的过滤器用变量W^{[1]表示。卷积的输出结果是一个4×4矩阵，它的作用类似于W}[1]*a^{[0]，然后加上偏差。这一部分（图中蓝色边框标记的部分）就是应用激活函数ReLU之前的值，它的作用类似于z}[1]，最后应用非线性函数（non-linearity），得到的这个4×4×2矩阵，成为神经网络的下一层，也就是激活层（activation layer）。

这就是a^[0]到a[1]的演变过程，首先执行线性函数，然后所有元素相乘做卷积，具体做法是运用线性函数再加上偏差，然后应用激活函数ReLU。这样就通过神经网络的一层把一个6×6×3的维度a^{[0]演化为一个4×4×2维度的a}[1]，这就是卷积神经网络的一层。

这个示例中有两个过滤器（两个特征），因此最终得到一个4×4×2的输出。如果我们用了10个过滤器，而不是2个，最后会得到一个4×4×10维度的输出图像，因为我们选取了其中10个特征映射。

假设你有10个过滤器，神经网络的一层是3×3×3，那么，这一层有多少个参数呢？下面来计算一下，每一层都是一个3×3×3的矩阵，因此每个过滤器有27个参数，然后加上一个偏差，用参数b表示，现在参数为28个。上一页幻灯片里有2个过滤器，而现在有10个，加在一起是28×10，也就是280个参数。注意一点，无论输入的图片多大，参数始终是280个。用这10个过滤器来提取特征，如垂直边缘，水平边缘和其它特征。即使这些图片很大，参数却很少，这就是卷积神经网络的一个特征，叫作“避免过拟合”。

1.4 池化层

除了卷积层，卷积网络也经常使用池化层来缩减模型的大小（reduce the size of their representation），提高计算速度（speed up computation），同时提高所提取特征的鲁棒性（robust），下面来看一下。

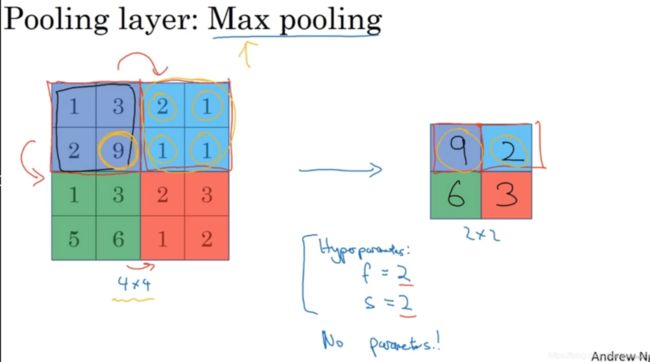
上面是池化层的例子，假设输入是4×4矩阵，池化类型是最大池化（max pooling）。执行最大池化的树池是一个2×2矩阵。执行过程非常简单，把4×4的输入拆分成不同的区域（不同区域用不同颜色来标记）。对于2×2的输出，输出的每个元素都是其对应颜色区域中的最大元素值。例如，左上区域的最大值是9，右上区域的最大元素值是2，左下区域的最大值是6，右下区域的最大值是3。这就像是应用了一个规模为2的过滤器，因为我们选用的是2×2区域，步幅是2，这些就是最大池化的超参数，即f = 2，s = 2。

这是对最大池化功能的直观理解，你可以把这个4×4输入看作是某些特征的集合，也许不是。你可以把这个4×4区域看作是某些特征的集合，也就是神经网络中某一层的非激活值集合。数字大意味着可能探测到了某些特定的特征，左上象限具有的特征可能是一个垂直边缘，一只眼睛，或是大家害怕遇到的CAP特征。显然左上象限中存在这个特征，这个特征可能是一只猫眼探测器。然而，右上象限并不存在这个特征。最大化操作的功能就是只要在任何一个象限内提取到某个特征，它都会保留在最大化的池化输出里。所以最大化运算的实际作用就是，如果在过滤器中提取到某个特征，那么保留其最大值。如果没有提取到这个特征，可能在右上象限中不存在这个特征，那么其中的最大值也还是很小，这就是最大池化的直观理解（intuition）。

必须承认，人们使用最大池化的主要原因是此方法在很多实验中效果都很好。

其中一个有意思的特点就是，它有一组超参数，但并没有参数需要学习。在实际操作中，一旦确定f和s，就是一个固定运算，梯度下降无需改变任何值。先看一下最终输出结果：

上图的例子，紫色区域的平均值是3.75，后面依次是1.25、4和2。这个平均池化的超级参数f = 2，s = 2，我们也可以选择其它超级参数。目前来说，最大池化比平均池化更常用。但也有例外，就是深度很深的神经网络，你可以用平均池化来分解规模为7×7×1000的网络的表示层，在整个空间内求平均值，得到1×1×1000。
现在总结一下，如上图，池化的超级参数包括过滤器大小和步幅，常用的参数值为f = 2，s = 2，应用频率非常高，其效果相当于高度和宽度缩减一半。也有使用f =3，s=2的情况。至于其它超级参数就要看你用的是最大池化还是平均池化了。最大池化时，往往很少用到超参数padding，当然也有例外的情况。假设没有padding，最大池化的输入和输出。
需要注意的一点是，池化过程中没有需要学习的参数。执行反向传播时，反向传播没有参数适用于最大池化。只有这些设置过的超参数（f,s），可能是手动设置的，也可能是通过交叉验证设置的。

池化层它只是计算神经网络某一层的静态属性（fixed function）。现在我们已经知道如何构建卷积层和池化层了。

二、文献阅读：BERT models for Brazilian Portuguese: pretraining, evaluation and tokenization analysis

2.1 摘要

使用神经网络进行语言表示的最新进展使得将大型预训练语言模型( LM )的学习内部状态转移到下游的自然语言处理( NLP )任务成为可能。这种迁移学习方法提高了在许多任务上的整体性能，并且在标记数据稀缺的情况下非常有益，使得预训练的LMs特别是有少量标注训练样本的语言具有宝贵的资源。在这项工作中，我们为巴西葡萄牙人训练了BERT (变压器的双向编码器表示)模型，我们将其命名为BERTimbau。我们在三个下游NLP任务上评估了我们的模型：句子文本相似度，文本蕴含识别和命名实体识别。我们的模型在所有这些任务中都提高了最先进的水平，超过了多语言BERT，并证实了大型预训练的葡萄牙语LM的有效性。

2.2 理论背景

本研究针对巴西葡萄牙语训练和评估了BERT模型，命名为BERTimbau，并应用于三个下游NLP任务：句子文本相似度、文本蕴含识别和命名实体识别。研究使用了brWaC语料库的数据进行BERTimbau模型的训练，该语料库是一个大规模且多样化的网页收集。预训练过程包括生成词汇表、预训练目标以及使用多样的文本进行额外的预训练。然后，模型在评估任务上进行了微调。此外，还进行了BERTimbau和mBERT分词分析，以了解它们对任务性能的影响。BERTimbau模型已经发布给社区，为未来的NLP研究提供了强大的基准。
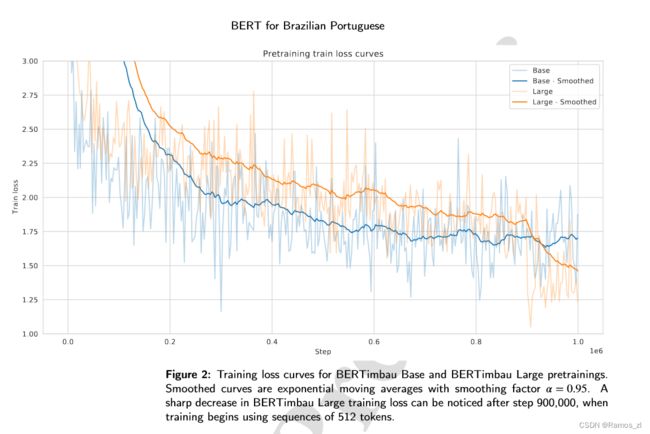
BERTimbau模型分为Base和Large两个规模，具有特定的参数和训练时长。模型使用学习率为1e-4和特定批量大小进行了100万步的预训练。权重使用了Multilingual BERT Base的检查点进行了初始化，对于BERTimbau Large模型使用了英文BERT Large的检查点进行了初始化。模型的训练损失曲线如图2所示。在微调阶段，采用特定的学习率调度、优化器实现和早停策略对完整模型进行微调。根据每个数据集的验证集选择最佳模型。

2.3 实验结果

BERTimbau模型在三个NLP任务上进行了评估：句子文本相似度（STS）、文本蕴含识别（RTE）和命名实体识别（NER）。在STS和RTE任务中，BERTimbau模型（特别是BERTimbau Large）表现出色，超过了Multilingual BERT（mBERT）和先前发表的结果。在NER任务中，作者尝试了两种NER架构：简单的线性分类器层和线性层后面跟随线性链条件随机场（CRF）层。最佳模型是BERTimbau Large与BERT-CRF相结合，取得了最先进的结果，并且在总体情况下的F1-score上比mBERT和先前的最佳结果有了显著的性能提升。

总结

填充、卷积步长和池化层是调整卷积神经网络性能和效率的关键因素。适当的填充有助于防止信息丢失，特别是在边缘区域。卷积步长的选择影响特征图的尺寸，需要在计算负担和信息保留之间取得平衡。池化层通过减小特征图的维度，提高计算效率，并增加模型的平移不变性。这些技术在设计卷积神经网络时需要根据具体问题进行合理的选择和调整，以达到更好的性能和泛化能力。