计算机图形学复习
第一章 绪论
1. 什么是计算机图形学
计算机图形学是借助计算机生成图形图像的艺术或科学
2. 计算机图形学研究内容
图形生成、图形变换、交互技术
3. 计算机图形学与数字图像处理的异同
相同点:像素层面图像和图形是一致的
不同点:处理过程是互逆的
计算机图形学是从目标描述产生图形显示
数值图像处理是对图像进行描述
第三章 图元生成
1. 直线生成算法:思路、判别参数定义
DDA算法
y = m x + b y k + 1 = y k + m s e t p i x e l ( x k + 1 , r o u n d ( y k + 1 ) ) y=mx+b \\ y_{k+1}=y_k + m \\ setpixel(x_{k+1},round(y_{k+1})) y=mx+byk+1=yk+msetpixel(xk+1,round(yk+1))
Bresenham算法
d 1 = y − y k d 2 = y k + 1 − y p k = Δ x ( d 1 − d 2 ) = 2 Δ y x k − 2 Δ x y k + C p k + 1 − p k = 2 Δ y − 2 Δ ( y k + 1 − y k ) p 0 = 2 Δ y − Δ x (可以理解为 1 , 0.5 带进去) d_1=y-y_k \\ d_2 = y_k + 1-y \\ p_k=\Delta x(d_1-d_2)=2\Delta y x_k-2\Delta x y_{k} + C \\ p_{k+1}-p_k=2\Delta y-2\Delta(y_{k+1}-y_k) \\ p_0=2\Delta y -\Delta x (可以理解为1,0.5带进去) d1=y−ykd2=yk+1−ypk=Δx(d1−d2)=2Δyxk−2Δxyk+Cpk+1−pk=2Δy−2Δ(yk+1−yk)p0=2Δy−Δx(可以理解为1,0.5带进去)
无乘法,无浮点运算
中点算法
f l i n e = a x + b y + c p k = f l i n e ( x k + 1 , y k + 1 2 ) p k + 1 − p k = a + b ( y k + 1 − y k ) p 0 = f l i n e ( x 1 + 1 , y 1 + 1 2 = a + 0.5 b ) f_{line}=ax+by+c \\ p_k = f_{line}(x_k+1,y_k+\frac{1}{2}) \\ p_{k+1}-p_k = a+b(y_{k+1}-y_k) \\ p_0=f_{line}(x_1+1,y_1+\frac{1}{2}=a+0.5b) fline=ax+by+cpk=fline(xk+1,yk+21)pk+1−pk=a+b(yk+1−yk)p0=fline(x1+1,y1+21=a+0.5b)
无乘法,无浮点运算
2. 圆的生成算法:思路、判别参数定义
Bresenham算法
d 1 = y k − y d 2 = y − ( y k − 1 ) d 1 ′ = y k 2 − y 2 d 2 ′ = y 2 − ( y k − 1 ) 2 p k = d 1 ‘ − d 2 ’ p k + 1 − p k = p 0 就是 ( 0 , R 2 ) 带进去 d_1=y_k-y\\ d2=y-(y_k-1)\\ d_1^{'}=y_k^2-y^2 \\ d_2^{'}=y^2-(y_k-1)^2 \\ p_k=d_1^{‘}-d_2^{’}\\ p_{k+1}-p_k=\\ p_0就是(0,R^2)带进去 d1=yk−yd2=y−(yk−1)d1′=yk2−y2d2′=y2−(yk−1)2pk=d1‘−d2’pk+1−pk=p0就是(0,R2)带进去
中点算法
f c i r c l e ( x , y ) = x 2 + y 2 − R 2 p k = f c i r c l e ( x k + 1 , y k − 0.5 ) p k + 1 − p k = p 0 带入 ( 0 , R ) 约为 1 − R f_{circle}(x,y)=x^2+y^2-R^2\\ p_k=f_{circle}(x_k+1,y_k-0.5) \\ p_{k+1}-p_k = \\ p_0带入(0,R)约为1-R fcircle(x,y)=x2+y2−R2pk=fcircle(xk+1,yk−0.5)pk+1−pk=p0带入(0,R)约为1−R
3. 椭圆的生成算法:思路、判别参数定义
中点算法
第一象限分两个区域
m = d y / d x = − ( 2 b 2 x ) / ( 2 a 2 y ) m=dy/dx=-(2b^2x)/(2a^2y) m=dy/dx=−(2b2x)/(2a2y)
f e l l i p s e ( x , y ) = b 2 x 2 + a 2 y 2 − a 2 b 2 p k = f e l l i p s e ( x k + 1 , y k − 0.5 ) p k + 1 − p k = p 0 带入 ( 0 , b ) 第二阶段 q k = f e l l i p s e ( x k + 0.5 , y k − 1 ) q 0 带入区域 1 终点 ( x 0 , y 0 ) , b 2 x 0 = a 2 y 0 f_{ellipse}(x,y)=b^2x^2+a^2y^2-a^2b^2\\ p_k=f_ellipse(x_k+1,y_k-0.5) \\ p_{k+1}-p_k = \\ p_0带入(0,b) \\ 第二阶段q_k=f_{ellipse}(x_k+0.5,y_k-1)\\ q_0带入区域1终点(x_0,y_0),b^2x_0=a^2y_0 fellipse(x,y)=b2x2+a2y2−a2b2pk=fellipse(xk+1,yk−0.5)pk+1−pk=p0带入(0,b)第二阶段qk=fellipse(xk+0.5,yk−1)q0带入区域1终点(x0,y0),b2x0=a2y0
4. 区域填充算法:思路
• 扫描转换法:按扫描线顺序确定每个点是否在区域内——边定义的多边形;
• 种子填充法:已知种子点,遍历区域内与种子点相连的点——边界点定义的多边形
扫描转换法
1.建立边表ET:(y_max,x_start,1/m,^)
2.建立有序边表SET:(y_max,x_start,1/m,^) 按y进行排序,相邻的就用指针指向
3.建立活性边表AET:(y_max,x_i+1,1/m,^)

种子填充法
第四章 样条曲线和曲面的生成
1. 三次 Hermit 曲线的多项式求解
2. Bezier 曲线的定义、混合函数的性质、casteljau 算法

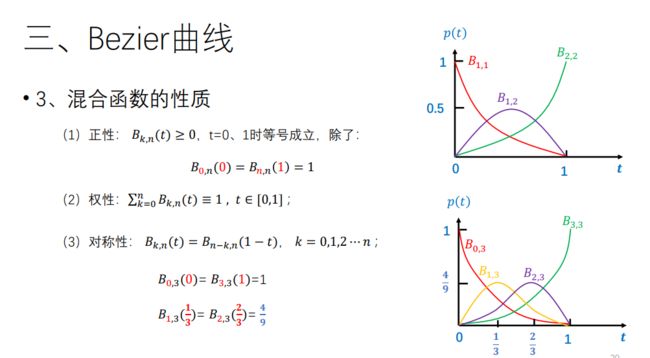


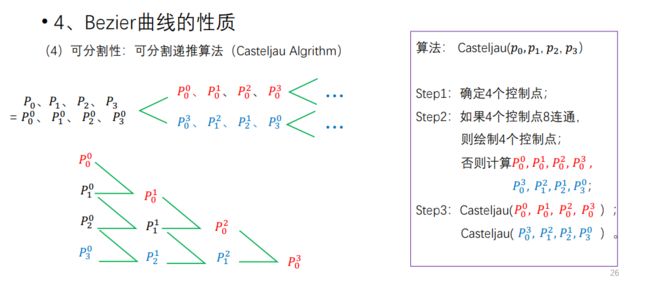
特点:
• 方便、简洁、有快速算法
• 不能局部调整
• 控制点的个数决定曲线多项式的次数
3. B 样条曲线的定义、B 样条曲线的性质
• B-样条曲线的参数多项式次数与控制点的个数无关;
• B-样条曲线不一定通过第一和最后控制点;
• 允许局部调整,代价是B-样条曲线的构造复杂;



4. 双线性曲面、单线性曲面、Coons 曲面的定义
第五章 分形图像生成
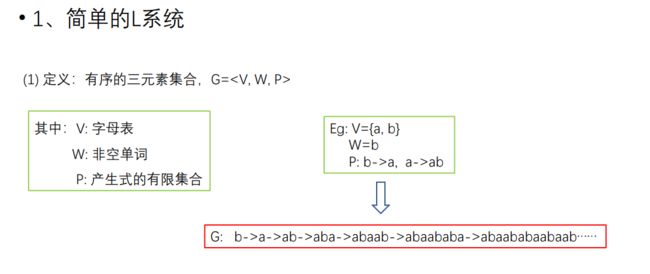
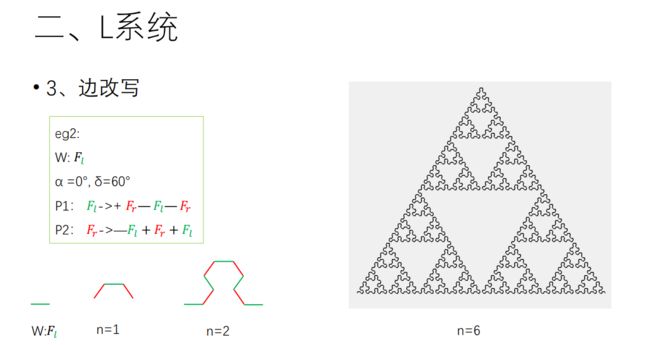
1. 基于 L 系统的分形生成方法
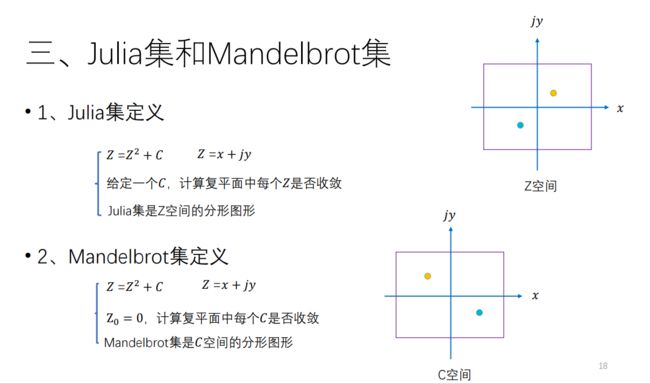
2. Julia 集和 Mandelbrot 集的生成方法
3. 迭代函数系统的分形生成方法
分形绘制的典型重要方法,在仿射变换的意义下,具有自相似结构,几何对象的整体被定义后,
选定若干仿射变换,将整体形态变换到局部,迭代进行,直到满意造型。


第六章 真实感图形生成
1. 多边形拟合表示、二次曲面表示、样条曲面表示及其法向矢量定义
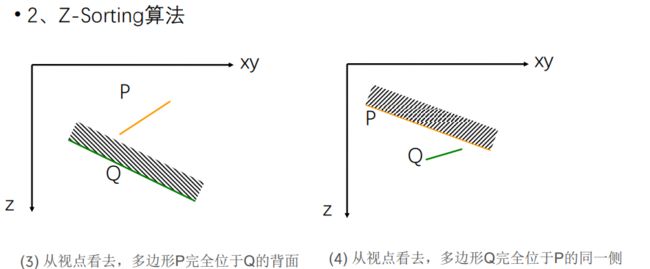
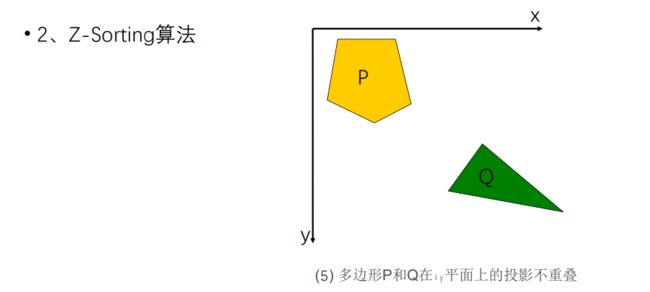
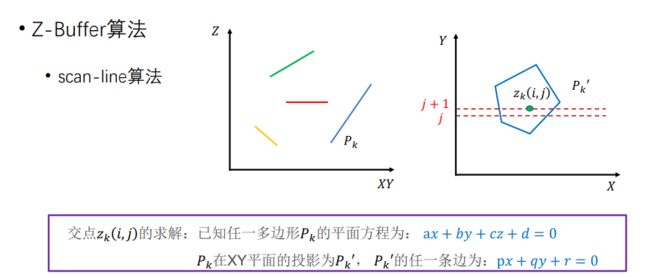
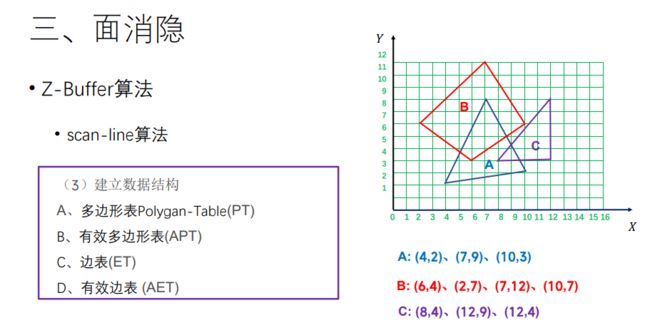
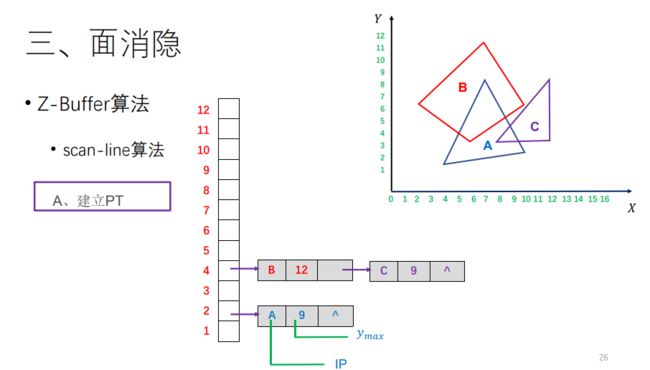
2. Z-sorting、Z-buffer 消隐算法思路
3. Phong 模型定义
4. 多边形明暗处理、光线跟踪、辐射度方法思路








反走样:光线跟踪算法的本质是对画面的点采样
加速技术:包围盒技术、空间分割技术
特点
• 绘制与消隐同时实现
• 模拟全局的漫反射和折射现象
• 计算量巨大:求交、逐点计算
• 与视线有关,换个方向,重新计算