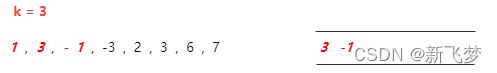滑动窗口最大值

给定一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。返回滑动窗口中的最大值。

示例 1：

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

示例 2：

输入：nums = [1], k = 1
输出：[1]

示例 3：

输入：nums = [1,-1], k = 1
输出：[1,-1]

示例 4：

输入：nums = [9,11], k = 2
输出：[11]

示例 5：

输入：nums = [4,-2], k = 2
输出：[4]

其实根据上面的示例和题目的描述，问题还是比较好理解的，从左向右，针对每个滑动窗口，求最大值。

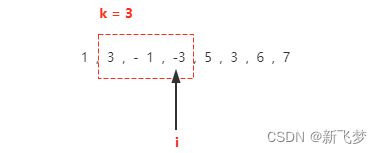
如上图所示，要解决这个问题，最先想到的最直观的方法就是，从左到右依次计算每一个滑动窗口的最大值，如上图所示，第一个滑动窗口的最大值就是 3 。

            

如上图所示，第二个滑动窗口的最大值也是 3 。以此类推，就可以获取到所有滑动窗口的最大值。

总共有 n - k + 1个滑动窗口，对于每一个滑动窗口，需要O( K )的时间复杂度求出最值，所以总的时间复杂度就是O((n-k+1)*k）= O(nk)，代码可以参考如下：

private static int[] maxSlidingWindow(int[] nums, int k) {
        int n = nums.length;
        int[] res = new int[n - k + 1];
        //依次处理每个滑动窗口
        for (int i = k - 1; i < n; i++) {
            int max = Integer.MIN_VALUE;
                //对每个滑动窗口求最大值
                for (int j = i; j >= i - k + 1; j--) {
                max = Math.max(max, nums[j]);
            }
            res[i - k + 1] = max;
        }
        return res;
    }

但是这样的代码在leetcode上运行是会超出时间限制的

通过前面的两个图，可以看到，对于两个相邻（只差了一个位置）的滑动窗口，它们共用着 k-1 个元素，而只有 1 个元素是变化的，但是前面的算法我们还是每一次都循环遍历当前滑动窗口以求取最大值，其实可以针对这里进行优化。

基于优先级队列的优化解法

我们知道，对于一个优先级队列（大顶堆），是可以在O（1）的时间复杂度内获取最大值的

对于本题而言，起始时将前 k个（即第一个滑动窗口）元素放入优先级队列（大顶堆）中，如下图所示，此时堆顶元素即为滑动窗口中的最大值。

当移动到下一个滑动窗口时，此时窗口中的新元素 -3 进入优先级队列，如下图所示

此时优先级队列的最大值还是 3 ，但是这个最大值是否还处于当前的滑动窗口中，需要进行一定的判断，通过一定的数学运算可知，向右处理的过程中，对于某个具体的索引 i ，滑动窗口的范围就是 [ i-k+1 , i ] 。如下图所示，所以我们最好在堆中存放值的下标和值

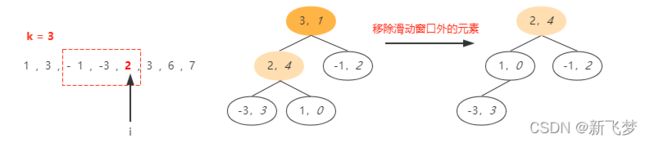
所以我们可以自定义优先级队列（大顶堆）的节点，使之可以存储具体的值和索引的形式，此处定义节点为（nums[i],i）这样的二元组。所以对于第二个滑动窗口就变为如下的形式。

此时就可以知道最大值为 3 ，索引为 1 的节点还是处于当前滑动窗口中，可以作为当前滑动窗口的最大值。

如下情况需要注意，我们把数组的值稍微变动一下，变为如下数组 

此时当向右移动一个值（即移动到下一个滑动窗口时），此时优先级队列中的最大值还是 3 ，但是最大值 3 已经不在当前滑动窗口范围内了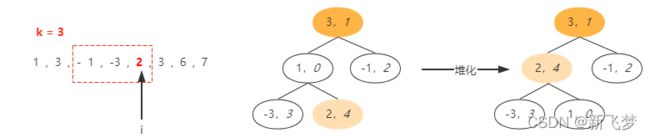 

所以需要从大顶堆中移除，此时堆会进行调整，从余下的元素中再次选出一个最大值作为堆顶元素，如此往复处理，直到堆顶元素在当前滑动窗口中

 其他的滑动窗口也是类似的。参考代码如下，结合上面的图说明和注释，是比较好理解的。

public int[] maxSlidingWindow(int[] nums, int k) {
        int n = nums.length;
        //节点存储一个数组，index = 0 表示nums[i] index = 1 表示 i
        PriorityQueue priorityQueue = new PriorityQueue<>(new Comparator() {
            @Override
            public int compare(int[] o1, int[] o2) {
                return o1[0] != o2[0] ? o2[0] - o1[0] : o2[1] - o1[1];
            }
        });

        //前k个元素进入队列
        for (int i = 0; i < k; i++) {
            priorityQueue.offer(new int[]{nums[i], i});
        }

        int[] ans = new int[n - k + 1];
        ans[0] = priorityQueue.peek()[0];

        //依次右移处理后面的滑动窗口
        for (int i = k; i < n; i++) {
            priorityQueue.add(new int[]{nums[i], i});
            //需要判断大顶堆的堆顶元素是否在滑动窗口内
            while (priorityQueue.peek()[1] <= i - k) {
                //如果堆顶元素已经不在滑动窗口内，则移除，移除会自动进行堆化
                priorityQueue.poll();
            }
            //堆顶元素已经在滑动窗口范围内了
            ans[i - k + 1] = priorityQueue.peek()[0];
        }
        return ans;
    }

空间复杂度是O（n），n表示数组的长度，当数组是升序排列时，最后所有元素都会进入到堆中。上面说过，当数组升序排列时，最终堆中会存储所有元素，往堆中插入一个元素的平均时间复杂度时O（lgn），n个元素都会进入堆，则总的时间复杂度就是O（nlgn）。

基于单调递减队列优化（可以看另外一篇关于单调栈简单应用的文章）思路

看上面基于优先级队列（大顶堆）的解决方案，根据堆的特性，获取大顶堆的堆顶元素可以用O（1）的时间复杂度，但是删除堆顶元素，或者是往堆中插入一个元素的时间复杂度都是O（lgn），因为加入或者删除一个元素时，需要进行堆化操作，以满足堆的特性。而且不在滑动窗口中的元素其实是没有必要继续存储在数据结构中的，但是对于堆来说，删除非堆顶元素就比较麻烦。下面看下基于单调递减队列的优化方案，还是以下面的数组进行说明

（1）起始时元素1进入队列，因为队列中没有任何元素，所以 1 有可能作为滑动窗口的最大值。

        

（2）接下来往右继续处理下一个元素 3 ，此时队列中有元素 1 ，元素 3 比元素 1 大，题目要求是求滑动窗口中的最大值，只要有 3 存在，元素 1 就不可能作为滑动窗口的最大值，当然也没有必要继续存储在队列中占着空间，这里说的 1 不可能作为滑动窗口的最大值是基于1 和 3 在同一个滑动窗口情况，当然 1 也可能作为 以 元素 1 为有边界的滑动窗口的最大值。3 进入队列后如下所示

        

（3）接下来处理元素 -1，因为 -1 比 3 小，所以 -1 进入队列，此处 -1 和 3均不能移除队列，因为元素 3 可能会作为元素 3 和 -1 所在同一个滑动窗口的最大值，元素 -1 可能作为以元素 -1 为左侧边界的滑动窗口的最大值，所以元素 -1 进入优先级队列后如下图所示

        

因为此时处理的元素已经有 k = 3 个，已经达到一个滑动窗口，所以要获取当前滑动窗口的最大值，最大值就是队头元素，所以直接取队头元素 3 即可，通过此处的分析可知，这个使用的数据结构要能实现 两头都可以插入和删除元素，所以此处使用双端队列。

（4）接下来处理 -3，队头元素还在当前滑动窗口中，所以都不移除，处理后如下图所示

（5）处理元素 2 ，此种情况需要注意，特别说明下，因为-1和-3比元素 2 小，所以需要移除元素 -1 和 -3 ，此处参照 上面第二步（2）的解释，移除 -1 和 -3 后如下图所示

但是此时对头元素 3 已经不在当前滑动窗口，由元素（-1，-3，2）组成的滑动窗口内，所以也需要移除掉，移除并获取最大值后的状态如下图所示。

其他的元素进入队列也是类似的，此处就不单独进行说明

特别说明：上面为了表述方便，双端队列里面都是直接展示出了元素，但是为了判断最大的元素是否超出了滑动窗口的边界，需要用到下标，索引，所以双端队列里面都是存储下表，其实道理是类似的

经上面分析，代码如下：

 private int[] maxSlidingWindow(int[] nums, int k) {
        int n = 0;
        if (nums == null || (n = nums.length) < k) return new int[]{};
        //定义双端队列，队列里面存储下标，即索引
        LinkedList dequeue = new LinkedList<>();
        int[] res = new int[n - k + 1];
        for (int i = 0; i < n; i++) {
            //保持栈的单调递减特性
            while (!dequeue.isEmpty() && nums[i] >= nums[dequeue.peekLast()]) {
                dequeue.pollLast();
            }

            //第i个元素进入队列
            dequeue.offerLast(i);

            //如果队头元素已经不在滑动窗口内，需要移除
            if (dequeue.peekFirst() <= i - k) {
                dequeue.pollFirst();
            }

            // 当已经有一个滑动窗口时，前几个元素，不够一个滑动窗口，不需要获取结果
            if (i + 1 >= k) {
                res[i + 1 - k] = nums[dequeue.peek()];
            }
        }
        return res;
    }

时间复杂度：O(n)，其中 n 是数组 nums 的长度。每一个下标恰好被放入队列一次，并且最多被弹出队列一次，因此时间复杂度为 O(n)。

空间复杂度：O(k)，与使用优先级队列不同的是，在此方法中使用的数据结构是双向的，因此「不断从队首弹出元素」保证了队列中最多不会有超过k+1 个元素，因此队列使用的空间为 O(k)。