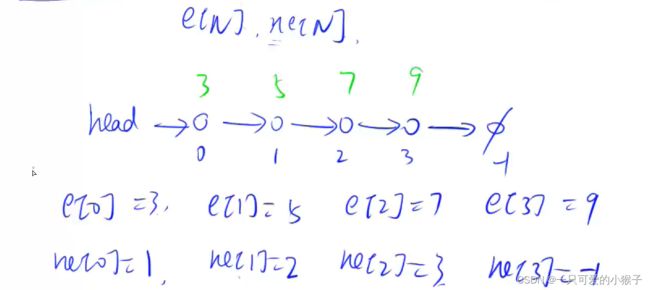AcWing算法学习笔记:数据结构(单链表 + 双链表 + 栈 + 队列 +单调栈 + 单调队列 + KMP + Trie + 并查集 + 堆 + 哈希表)
数据结构
- 一、单链表⭐
- 二、双链表⭐
- 三、栈
-
- ①模拟栈⭐
- ②表达式求值 (还没写)
- 四、模拟队列
- 五、单调栈⭐
- 六、单调队列(滑动窗口)⭐
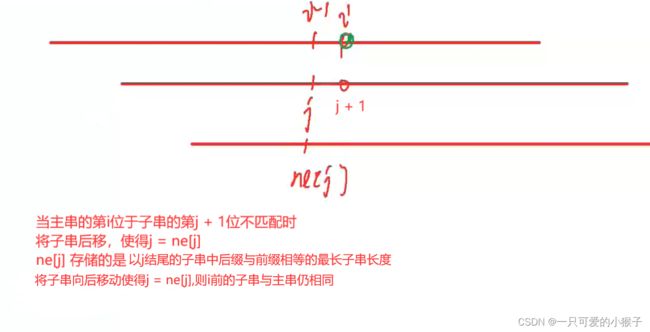
- 七、KMP字符串⭐⭐
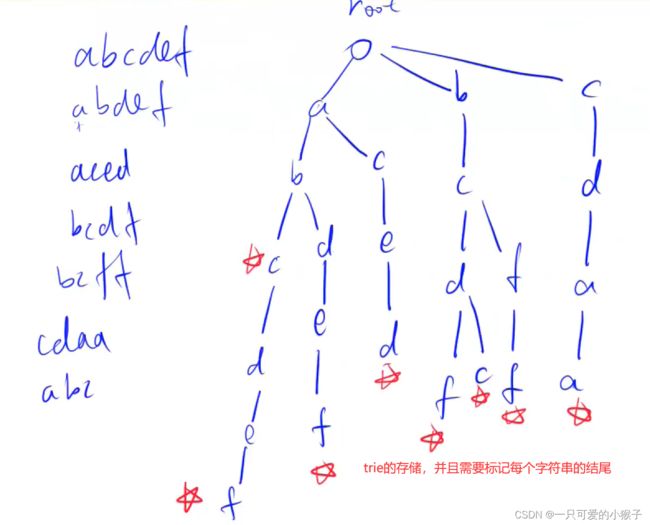
- 八、Trie
-
- ①Trie字符串统计⭐
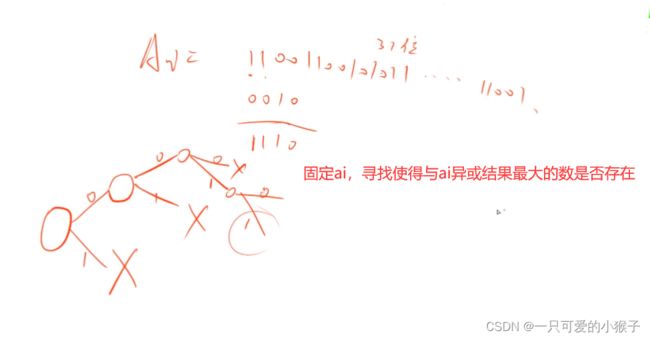
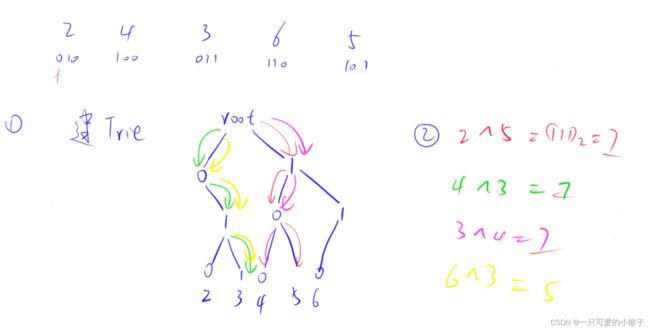
- ②最大异或对⭐
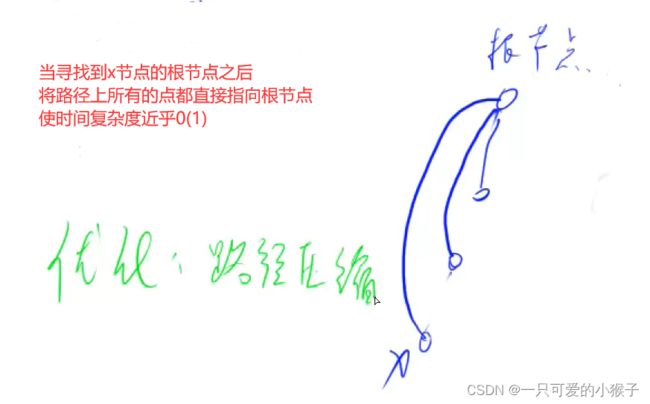
- 九、并查集
-
- ①合并集合
- ②食物链
- 十、堆
-
- ①堆排序
- ②模拟堆(还没写)
- 十一、哈希表
-
- ①模拟散列表
- ②字符串哈希
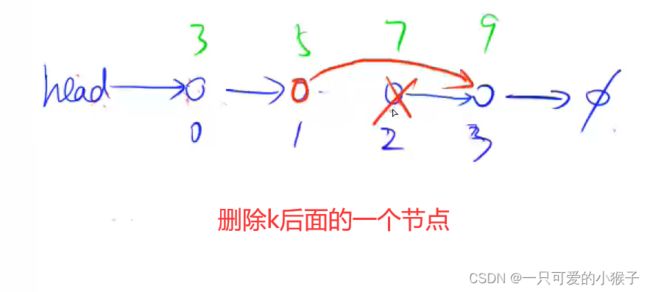
一、单链表⭐
时间复杂度
插入删除节点0(1)
查询节点0(n)
代码
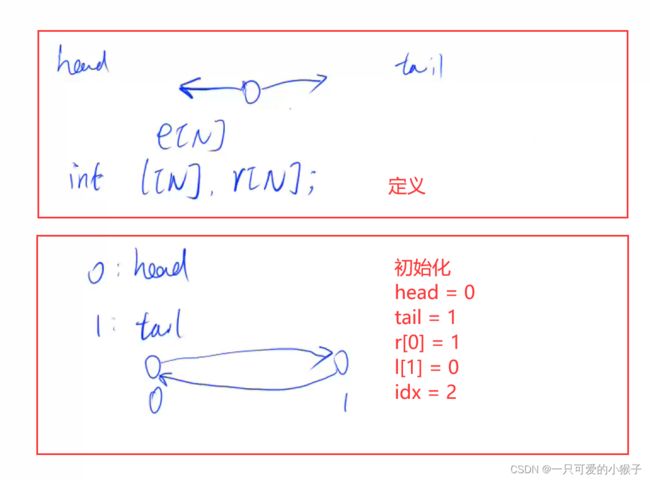
#include 二、双链表⭐
代码
#include 三、栈
①模拟栈⭐
代码
#include ②表达式求值 (还没写)
算法
代码
四、模拟队列
代码
#include 五、单调栈⭐
代码
#include 六、单调队列(滑动窗口)⭐
代码
#include 七、KMP字符串⭐⭐
#include 八、Trie
①Trie字符串统计⭐
代码
#include ②最大异或对⭐
代码
#include 九、并查集
①合并集合
算法

代码
#include ②食物链
代码
#include 十、堆
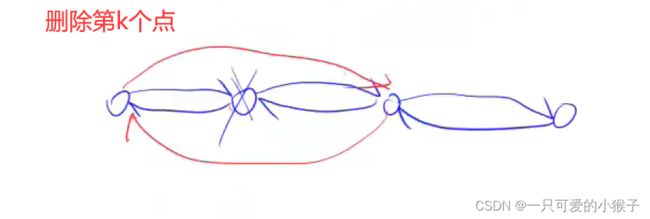
①堆排序
算法
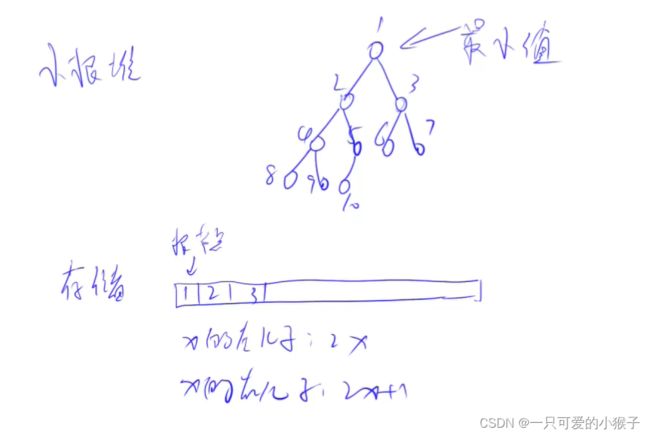

初始建堆,若采用插入的方法,则时间复杂度为0(nlogn)
优化方法:将所有元素先乱序存入数组(建立起一个乱序完全二叉树),然后对这棵树的前n/2个元素进行一遍down操作,即可构成堆
该优化方法由下图的证明可以得出时间复杂度为0(n)

代码
#include ②模拟堆(还没写)
算法
代码
十一、哈希表
①模拟散列表
算法

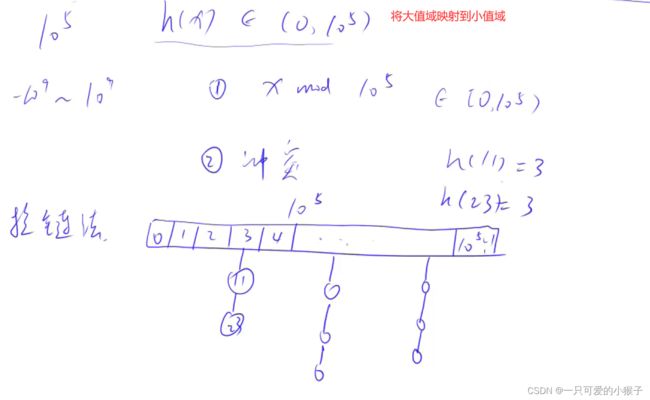
并且取模的这个数需要是质数,并且尽可能离二的整次幂尽可能的远,这样发生冲突的概率是最小的

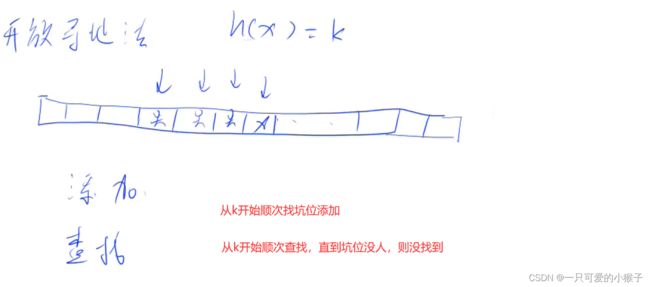
这两种方法的删除操作都是开一个数组标记,不会真正进行删除
总结如下

代码
********拉链法********
#include ②字符串哈希
代码
#include