论文笔记-vChain: Enabling Verifiable Boolean Range Queries over Blockchain Databases

核心方法：

提出了一种基于累加器的可认证数据结构，可以动态聚合任意查询属性
提出块内和块间索引，聚合块内和块间数据，可以做高效查询验证
倒排前缀树结构，加速同时处理大量数据的订阅查询

提出问题：

1.range查询
2.布尔查询
3.没有可靠第三方、而且不能保证查询的完整性

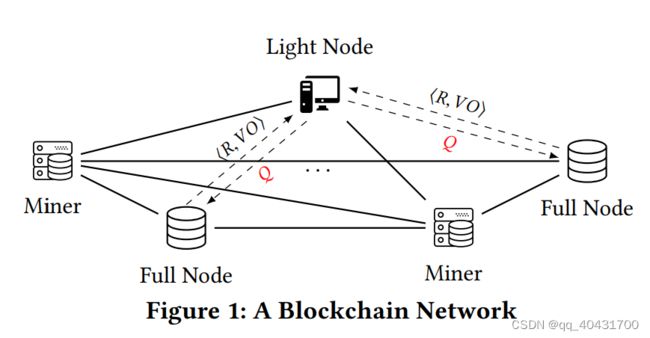
图中元素有：
①全节点
②矿工节点：是全节点，而且负责构建共识证明，比如计算nonce
③轻节点：存nonce、区块的哈希，不存数据记录
提出的Vchian是可验证查询的，在全节点（不可信）构造ADS，ADS生成VO，VO给用户来验证查询结果
Q代表query，返回给用户（即轻节点）

Vchain的框架来自于外包数据库的查询认证技术，但有一些不符合
1.区块链没有DO，没人给ADS签名，只有矿工根据共识协议构造共识证明才能把新数据附加到区块链，但矿工不能持有私钥并签名
2.传统ADS数据集固定，区块链是无界的
3.传统外包数据库中，ADS根据需要随时创建和附加，以支持涉及不同属性集的更多查询，但对于动态查询属性，一种不变的ADS更适用

综上
1.提出了一种基于累加器的ADS，可以对数值属性和集值属性动态聚合
2.这个ADS独立于共识协议，所以与当前区块链技术兼容
3.基于这个ADS开发了高效可验证查询的算法
4.块内和块间索引，实现批量验证
5.对于大规模订阅查询，提出了一种查询索引方案，对相似的查询请求做合并

已有查询：
①基于VC(电路)的，可以支持任意计算任务，但有预处理，且预处理时，需要把证明key和验证key硬编码到数据和查询任务里
解决：SNARKs的变体，预处理步骤取决于数据库和查询程序的上限

②vSQL，使用交互式协议支持可验证的SQL查询，但只限于有固定模式的关系型数据库 基于ADS的，适用于特定查询。 经常使用：数字签名和MHT
==>数字签名，用非对称加密验证数字信息的内容。对于可验证查询，要对每个数据记录签名，所以无法扩展到大型数据库
==>MHT，建立在分层树上，DO只要给根摘要签名，就可以验证数据记录的任何子集。所以MHT已经广泛适用于各种索引结构，已经研究过其用于集值属性的可验证查询

③数据流的可验证查询，基本是一次性的查询，检索最近一次版本的流数据，DO要为所有数据记录维护一棵MHT，延迟长，不适合实时数据流服务
数据流的订阅查询，还没有关于区块链的订阅查询的完整性问题分析

问题定义

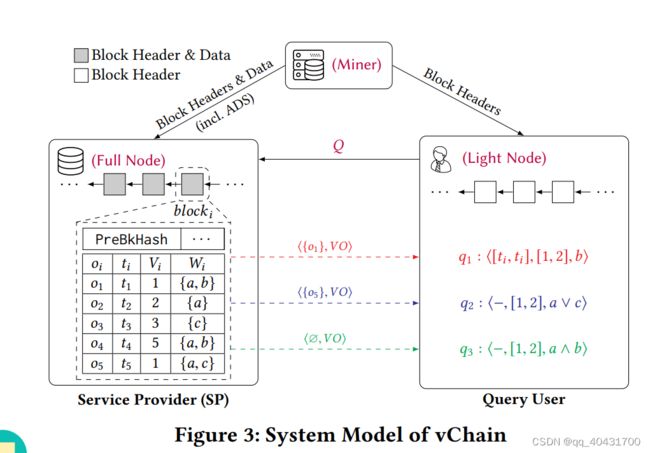
{o1, o2, · · · , on}
⟨ti,Vi,Wi⟩
ti：timestamp
Vi：表示一个或多个数值属性的多维向量
Wi：集值属性

矿工给每个块嵌入ADS

考虑时间窗口查询和订阅查询
1.时间窗口查询：（用户搜索在某个时间段内出现的记录）
查询 q = ⟨[ts, te], [α, β], ϒ⟩
[ts, te] 时间范围选择谓词
[α, β] 多维范围选择谓词，是数值属性的多维范围选择谓词
ϒ 单调布尔函数，是集值属性的单调布尔函数
返回O要满足 {oi = ⟨ti,Vi,Wi⟩ | ti ∈ [ts, te]∧Vi ∈[α, β] ∧ ϒ(Wi) = 1}
我们假设ϒ是一个合取范式CNF
举例：比特币系统中，Vi就是转账的金额，Wi就是地址集，包含接收方和发送方，有查询q=⟨[2018-05, 2018-06], [10, +∞], send:1FFYc∧receive:2DAAf⟩，表示要查的是从2018年5-6月间，交易金额≥10，地址集是发送方为1FFYc且接收方为2DAAf

2.订阅查询（用户注册自己感兴趣的查询）
查询 q = ⟨−,[α, β], ϒ⟩
SP会持续返回所有满足条件的O，{oi = ⟨ti,Vi,Wi⟩ | Vi ∈[α, β] ∧ ϒ(Wi) = 1} ，直到查询被注销
举例：基于区块链的汽车租赁系统，每个租赁对象的Vi存租赁价格，Wi存一组文本关键字，一个用户会订阅一个查询q = ⟨−, [200, 250], “Sedan” ∧ (“Benz” ∨ “BMW”)⟩来接收所有富和条件的信息，即价格在200-500之间，并且包括了关键词Sedan和Benz或BMW

问题：SP不可信
解决：让SP证明查询结果的完整性。在查询处理过程中，让SP检查嵌入在链上的ADS，构建一个VO，包含结果的验证信息。VO连同结果一起返回给user。user可以利用VO确定查询结果的soundness和completeness
soundness：查询结果没有被篡改，都满足查询条件
completeness：结果没有丢失和遗漏

主要挑战：ADS怎样设计能容纳于区块链系统，使VO传输和验证的开销小

Cryptographic Multiset Accumulator密码多重集累加器： acc(·)，用来证明集合不相交
几个函数：
• KeyGen(1λ) → (sk,pk): 1λ 安全参数，sk 私钥，pk 公钥
• Setup(X,pk) → acc(X ): X 多重集，acc(X ) 累加值
• ProveDisjoint(X1, X2,pk) → π: 输入pk、两个多重集X1和X2，如果它们交集为空，就输出一个证明π.
• VerifyDisjoint(acc(X1), acc(X2), π,pk) → {0, 1}: 当且仅当X1 ∩ X2 = ∅时输出1

Basic Solution

如果把MHT作为ADS，有一些缺点
1.树建立后只支持键查询，如果涉及到任意属性集的查询，要建指数级别的树
2.不适用于集值属性（因为不适用于合取范式？）
3.不能有效聚合，块间优化难做

新的ADS是基于累加器的，把数值属性转换为集值属性，支持任意查询属性的动态聚合

论文内容
5.1 5.2 考虑单个object的布尔时间窗口查询
5.3 扩展到范围查询
6 多个object的批量查询和验证
7 订阅查询

5.1 ADS生成和查询过程
只考虑集值属性（析取合取），即oi = ⟨ti,Wi⟩，用ObjectHash表示原来块里的MerkleRoot
①ADS生成
在原来区块增加attdigest字段
attDigest需要有三个属性
1.attDigest需要把一个object的Wi总结，并且可以证明这个object匹不匹配查询条件。如果不匹配，就只要返回这个digest而不是整个object
2.不管Wi里有多少个元素，attDigest大小要恒定
3.要可以聚合，支持块内和块间批量验证
所以把多重集累加器作为attDigest，AttDigesti = acc(Wi) = Setup(Wi,pk)

②可验证查询过程
匹配：把object作为结果返回验证，根据头里的ObjectHash可以验证完整性，对轻节点友好
不匹配：把查询的合取范式里的布尔函数看成集合列表，比如 “Sedan” ∧ (“Benz” ∨ “BMW”)看成两个集合 {“Sedan”} 和 {“Benz”, “BMW”}
考虑
object oi : {“Van”, “Benz”}
单个对象可验证查询算法如下：

1.查询 q= “Sedan” ∧ (“Benz” ∨ “BMW”)
2.不匹配，因为对于{“Sedan”}这个集合，object里就不存在
3.用ProveDisjoint({“Van”, “Benz”}, {“Sedan”},pk)生成π作为不相交证明，也就是不匹配的object的VO
4.用户检索块头的AttDigesti = acc({“Van”, “Benz”})，然后用VerifyDisjoint(AttDigesti, acc({“Sedan”}), π, pk)来验证不匹配

把这个算法扩展到时间窗口查询：
先找到时间戳在查询窗口里的对应区块，然后为这些选定块里的每个object重复调用算法1
考虑
q= “Sedan” ∧ (“Benz” ∨ “BMW”)
o1: {“Sedan”, “Benz”},
o2: {“Sedan”, “Audi”},
o3: {“Van”, “Benz”},
o4: {“Van”, “BMW”}.
发现o2与“Benz” ∨ “BMW”不匹配，o3和o4与“Sedan”不匹配
o1匹配，会直接返回这个object

5.2 多重集累加器的结构（前面说的AttDigest有两种结构）
1.基于双线性对和q-SDH假设，有以下算法
①KeyGen(1λ) → (sk,pk) ：(p, G, H, e, g)是一个双线性对，sk = (s)， s ← Zp，pk = (g,gs,gs 2, · · · ,gsq ) g的s的q次方
②Setup(X,pk) → acc(X )：多重集 X = {x1, · · · , xn}的累积值acc(X )等于…，见原文，因为多项式插值的性质，他可以在不知道私钥的情况下计算出来
③ProveDisjoint(X1, X2,pk) → π：根据扩展的欧几里得算法，如果X1 ∩ X2 = ∅，那么就存在两个多项式Q1, Q2使得 P(X1)Q1 + P(X2)Q2 = 1， π = (F ∗1 , F ∗2 ) = (дQ1,дQ2). 格式有问题 见原文
④VerifyDisjoint(acc(X1), acc(X2), π,pk) → {0, 1}：证明有效输出1

2.引入两个额外的原语， Sum(·) 和 ProofSum(·) ，可以聚合多个累加值、聚合多个不相交证明，基于双线性对和q-DHE假设，有以下算法
①KeyGen(1λ) → (sk,pk)
②Setup(X,pk) → acc(X)：同样可以在不知道私钥的情况下通过多项式插值计算出acc
③ProveDisjoint(X1, X2,pk) → π
④VerifyDisjoint(acc(X1), acc(X2), π,pk) → {0, 1}
⑤Sum(acc(X1), acc(X2), · · · , acc(Xn)) → acc(Σni Xi) X1到Xn的和的acc
也就是多个多重集的acc
⑥ProofSum(⟨π1, Xπ1,1, Xπ1,2⟩, · · · , ⟨πn, Xπn,1, Xπn,2⟩) → π ′
其中π1 = ProveDisjoint(Xπ1,1, Xπ1,2, pk)，…，
πn = ProveDisjoint(Xπn,1, Xπn,2,pk)
当且仅当Xπ1,2 = Xπ2,2 = · · · = Xπn,2时，输出可以聚合成π ′，也就是π1到πn的和
π ′是多个多重集与同一个多重集都不相交的证明
问题：会导致公私钥变大
第一种公钥大小与最大多重集大小是线性关系，第二种与整个系统中最大可能属性值是线性关系
现实生活中是先把属性值哈希成一个几百位的整数，然后被累加器接受，所以提前生成和发布这样的公钥代价很高，引入一个oracle，拥有私钥，负责回答公钥的请求，可以用可信第三方或者硬件执行

5.3扩展到范围查询（前面都在说集值属性的布尔查询）

先介绍
怎么把数转换成二进制前缀元素
把数值属性转化为集值属性，范围查询就被映射成布尔查询
1.用二进制表示每个数
2.再转化成一组二进制前缀元素
比如4是100，trans(4) = {1∗, 10∗, 100}，*是通配符
对于数值的向量，每个维度都这样表示
比如向量(4, 2)是(100, 010)，表示成{1∗1, 10∗1, 1001, 0∗2, 01∗2, 0102}，末尾的1和2是下标，用来区分维度

再介绍
把范围转换成单调布尔函数，用一棵构建在整个二维空间的二叉树。

举例一个一维空间的二叉树

①对于一维范围 [α, β]
1.用二进制格式表示 α和β
2.把二进制格式的α和β看成树里的两个叶节点，然后用最少的节点集合表示这个范围
转换后的布尔函数是用OR (∨)来连接集合里的每个元素
比如查询范围[0, 6]，转换后的布尔函数就是 0 ∗ ∨10 ∗ ∨110（见Fig5），等价集合就是{0∗, 10∗, 110}
②对于多维范围，转换后的布尔函数就是用AND (∧)来连接每个维度的布尔函数
比如范围[(0, 3), (6, 4)]可以被转换成(0∗1 ∨ 10∗1 ∨ 1101) ∧ (0112 ∨ 1002)等价于集合{0∗1, 10∗1, 1101} 和 {0112, 1002}. （这里两维范围分别是0_6和34）

综上，查询vi在不在范围 [α, β]里变成了布尔查询：vi的变换前缀集和 [α, β]等价集是否相交
比如4 ∈ [0, 6] ，变成
{1∗, 10∗, 100}∩{0∗, 10∗, 110} = {10∗} ≠∅
比如(4, 2) 不属于 [(0, 3), (6,4) （a,b）可以看成列向量
等价集{0112, 1002}（也就是3~4这个范围） ， {0112, 1002} ∩ {1∗1, 10∗1, 1001, 0∗2, 01∗2, 0102} = ∅，所以不属于

所以，对于
object ⟨ti,Vi,Wi⟩就变成了 ⟨ti,W ′i ⟩，W ′i = trans(Vi) +Wi
查询q = ⟨[ts, te], [α, β], ϒ⟩变成了 ⟨[ts, te], ϒ′⟩，ϒ′ = trans([α, β]) ∧ ϒ
查询结果就变成了{oi =⟨ti,W ′i ⟩ | ti ∈ [ts, te] ∧ ϒ′(W ′i ) = 1}

BATCH VERIFICATION

介绍两种index和一个在线批量验证方法，让SP可以为不匹配的objects提供批量证明

6.1块内索引

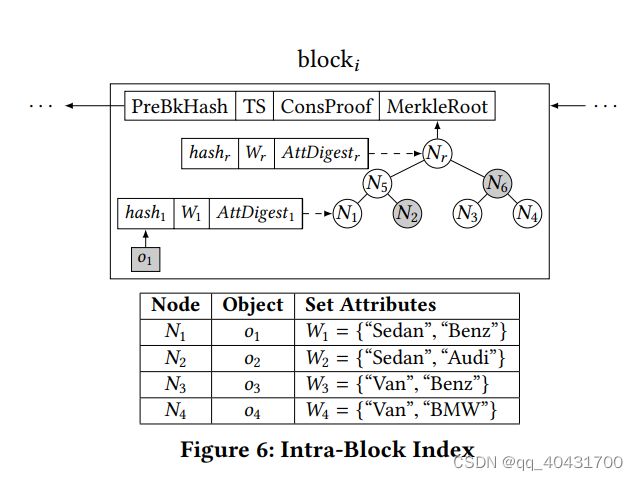
Fig6 展示的是具有块内索引的一个块
把每个object的ObjectHash和AttDigest组织到了一个二叉Merkel树里，块头的MerkleRoot里就是这棵树的根哈希。
每个节点三个字段，child hash（用hashi表示，用于形成MHT）、attribute multiset（用Wi表示）和attribute multiset的累积值（用AttDigesti表示），都是从子节点计算出来的。
①非叶节点的这三个字段
• Wn = Wnl ∪ Wnr
• AttDigestn = acc(Wn)
• hashn = hash(hash(hashnl | hashnr ) | AttDigestn)
②叶节点的这三个字段
与底层对象的字段相同

使证明效率最大化，就是最大化提高使不匹配对象一起修剪掉的机率
1.找到一种聚类策略，在给定一个用户的查询请求时，使一个节点不匹配这个请求的机率最大，也就是最大化每个节点下对象的相似性
2.选用平衡树，提高查询效率

提出的块内索引是矿工自下而上基于块的数据对象构建的（算法2：块内索引的构造）

1.给块内每个对象分配一个叶节点
2.产生最大Jaccard相似度叶节点迭代合并
（nl和nr不同）

把一个查询请求转化成了树搜索
从根节点开始：
①如果当前节点的属性多重集满足查询情况，就继续查它的子树，
同时对应的attDigest加入VO，在结果验证的时候用来重构MerkelRoot
②如果不匹配，意味着它的子树都不满足，这时SP调用ProveDisjoint(·)，用对应的attDigest生成不匹配证明，
③直到叶节点，多重集满足查询条件的object就是匹配的object，作为查询结果返回
（算法3：使用块内索引的VO的构造）

举例：Fig6的表格，o1~o4

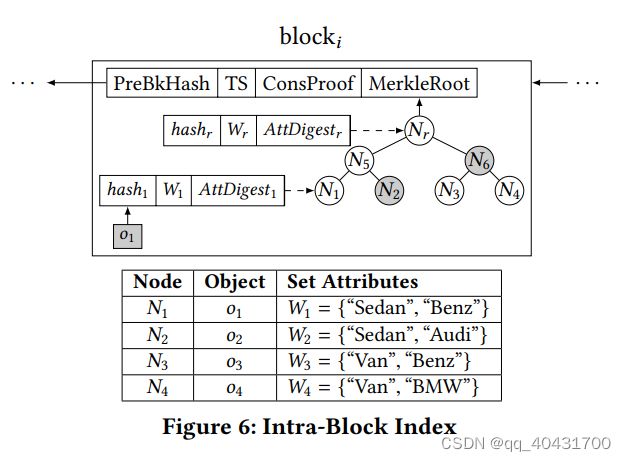
q： “Sedan” ∧ (“Benz” ∨ “BMW”)
查询过程：简单地把索引从根节点遍历到叶节点
结果R是{o1}
SP返回的VO是{⟨AttDiдestr ⟩, ⟨AttDiдest 5⟩, ⟨hash2, π2, {“Audi”}, AttDiдest 2⟩, ⟨hash6, π6, {“Van”}, AttDiдest 6⟩}

验证过程：
用户调用VerifyDisjoint(·)，参数就是attDigest、不相交集、VO里的π
验证查询结果的健全性和完整性，要重构MerkelRoot，然后与块头的比较
1.VerifyDisjoint(·)先用⟨π2, AttDigest 2, {“Audi”}⟩ and ⟨π6, AttDigest 6, {“Van”}⟩ 验证N2和N6确实不匹配
2.用户用收到的result里的o1和VO里的东西计算hashr
hash5 = hash(hash(o1) | hash2 | AttDiдest 5)
hashr = hash(hash5 | hash6 | AttDiдest r )
3.用户把计算得到的hashr和自己块头的MerkelRoot比较

6.2块间索引

Fig7，块间索引由多个跳跃组成
使用跳表，每次跳过指数数量的以前的块，也就是可能会跳过2，4，8，…个块
每次跳跃，维护三个组件：
1.PreSkippedHash Lk：跳过的所有块的哈希
2.W Lk：跳过块的属性多重集的总和
3.AttDigest Lk：W Lk 对应的累加值
使用属性多重集的总和来实现在线可验证聚合
最后在块头多写一个字段SkipListRoot，字段计算方式见原文

实际查询时，一个skip表示由于相同原因而不匹配的多个块

（算法4：使用块间索引的查询过程）

1.从查询时间窗口的最新块开始，从最大到最小迭代跳过
2.如果一个跳过WLi全不满足查询条件，这表示跳过的块都不匹配，调用ProveDisjoint(·)输出不匹配证明πi
3.⟨PreSkippedHash Li , πi, ϒi, AttDigest Li ⟩添加到VO，以提供给用户验证
4.除了hash Li，其他哈希也添加到VO（属于SkipList的hash）
5.如果迭代过程没找到不匹配的，就调用块内索引检查前一个块
6.如果找到了不匹配的，就相应检查它前面一个块
7.递归调用InterIndexQuery(·)直到检查完时间窗口里的所有块

在线批量验证

使用Sum(·)，块内不同子树或者块间的索引块内都是因为不匹配同一个集合，这样可以减少调用函数（生成证明和验证的函数）的次数，减少VO存储。

订阅查询

订阅查询
每看到一个新确认的区块，SP就要把结果和VO一起发送给注册用户

7.1 提出一个查询索引，高效处理大量订阅查询
7.2 延迟可认证优化，延迟不匹配证明以降低查询验证成本

7.1可扩展处理的查询索引

查询处理的主要开销来自SP对不匹配对象的证明的生成
不同的订阅查询可能有相同的不匹配原因，这类查询可以共享不匹配证明（怎么共享的？）

所以使用倒排前缀树 IP-Tree，实际上就是一个参考了倒排文件的前缀树
倒排文件有数值范围条件的和布尔集条件的（怎么倒排的？）

为了索引所有在是订阅查询的数值范围，IP-Tree是在网格树基础上构建的，每个树节点由CNF布尔函数表示
[(0, 3), (6, 4)]被表示为(0∗1 ∨ 10∗1 ∨ 1101) ∧ (0112 ∨ 1002)

前缀树、倒排文件（数值范围文件RCIF和布尔函数文件BCIF）
文件根据索引的订阅查询建立
RCIF用于检查数值范围查询不匹配
BCIF，只有完全覆盖才记录，用于检查布尔集不匹配

构建IP-Tree：（Fig.8）

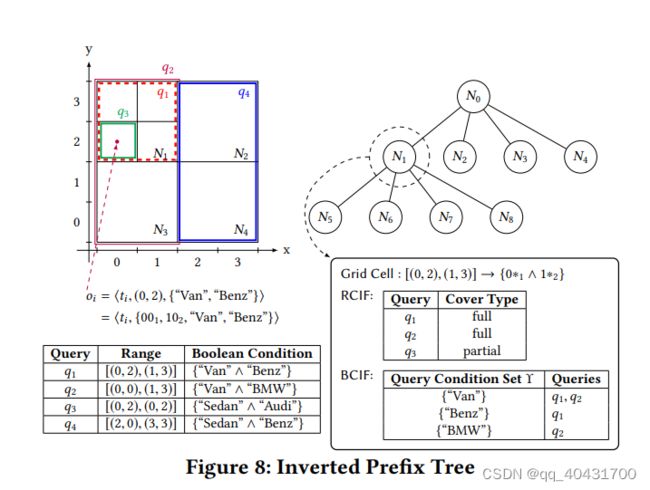
SP自上而下构建
1.创建根节点，把所有查询作为部分覆盖加入RCIF
2.拆分根节点创建4个等大的子节点
3.对每个子节点，如果一个范围查询部分或全部覆盖了节点空间，就加到这个节点的RCIF里；只有全覆盖的等价布尔集加入BCIF（例子里把^的查询条件的拆开写，，这样就是合并最相似？），部分覆盖的要进一步拆分（全覆盖指q把N全覆盖到了）

算法停止条件：在所有叶节点里都没有部分覆盖的查询
更新方法：当一个查询注册或注销，根据查询的数值范围更新 IP-Tree 的节点。如果有必要，可以拆分或合并节点。
防止树过深：超过设定阈值时返回到没有IP-Tree的时候

有了IP-Tree，可以把订阅索引变成树的遍历
举例：（这是订阅查询过程，这棵树怎么建立的、查询怎么插入的、新来的o去哪）
1.当一个新o到达时，IP-Tree遍历从根到叶节点中覆盖了o的节点的路径
2.对遍历路径上的所有结点nq，都可以从nq的RCIF里找到相关的查询
3.查询可以被分为3类
①全覆盖的查询，查询的等价集s在nq的BCIF里匹配o，o作为查询的结果添加
②全覆盖的查询，查询的等价集s在nq的BCIF里不匹配o，ProveDisjoint(·)被调用并生成不相交证明
③部分覆盖的查询，无需进一步操作
4.辨认出现在nq的父节点的RCIF但不出现在nq的RCIF，这种和o的数值范围查询就不匹配，也生成不相交证明
5.处理nq的子节点，直到到达了叶节点，或者所有的查询都被分类成匹配或者不匹配

考虑：（Fig.8）
新oi = ⟨ti, (0, 2), {“Van”, “Benz”}⟩ = ⟨ti, {001, 102, “Van”, “Benz”}⟩
对于这个新o，怎么确认q匹配还是不匹配，什么时候确认？
树，从上往下遍历，包含o的结点N，比对其RCIF和BCIF

怎么把订阅查询扩展到块内索引？有什么不同？
从块内索引的根开始。
如果一个查询全覆盖，而且匹配，不能直接返回这个N作为查询结果，而是递归检查子节点，直到叶节点（因为订阅查询是查新来的O是否属于已注册的q，块内查询是查输入的q与块内的O是否匹配）

Lazy Authentication

在之前的部分，结果和证明会在新区块确认的时候就同步更新发布给注册用户了，而且查询都不匹配的时候也会计算和发送不匹配证明，这种方法适用于实时应用程序。

Lazy Authentication
对没有实时性要求的程序，SP仅在有匹配对象时返回，或者时间超过阈值。
所以，VO要证明：当前对象要匹配，自上次结果以来其它对象都不匹配
做法：等待匹配结果，调用时间窗口查询实时计算不匹配证明
（时间窗口查询：用户搜索在某个时间段内出现的记录）
但这样只能给每个查询单独生成不匹配证明，不能利用不同订阅查询分享的证明（时间窗口查询不能利用）；而且因为只有匹配的时候算证明，有计算压力

解决：利用块间索引逐步生成不匹配证明

使用块内索引回答订阅查询和时间窗口查询完全不同。
时间窗口查询：可以回溯区块链，用跳表聚合证明（文章里面到底提了几种聚合？？）
订阅查询里不行，因为新区块还不可用，我们不知道未来的object是否共享相同的不匹配证明；
引入了一个堆栈，帮助跟踪共享相同不匹配的条件的新来的块
用跳表找到最大跳跃距离Li，这样它覆盖栈顶的m个元素
这些块的attDigests用attDigesti Li代替，不相交的证明可以调用ProofSum(·)来聚合。
比如：在堆栈中有两个不匹配的 blocki 和 blocki-1，有一个距离为 2 的跳跃，SP 可以用从 ProofSum(πi, πi−1) 计算的聚合证明替换他们的证明。
即：找到匹配结果时，SP 不需要从头开始计算集合的不相交证明
算法5

论文笔记仅为个人观点，仅供参考