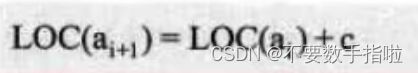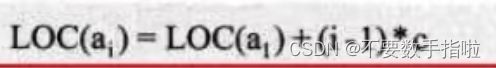线性表的顺序储存结构
线性表的定义
线性表:零个或多个数据元素的有限序列。
序列,说明元素之间是有顺序的,若元素存在多个,则第一个元素无前驱,最后一个元素无后继,其他元素都有且仅有一个前驱和后继。
所以线性表的个数n(n>=0)定义为线性表的长度,当n=0时,称为空表。
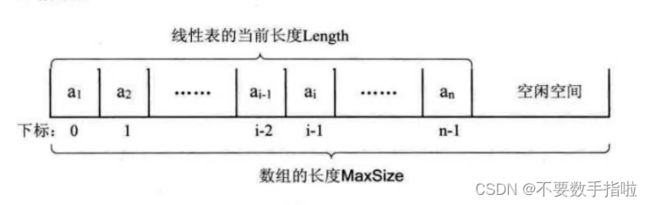
在非空表中的每个数据元素都有一个确定的位置,如a1是第一个数据元素,an 是最后一个数据元素,ai是第i个数据元素,称i为数据元素a在线性表中的位序。
在较为复杂的线性表中,一个数据元素可以由若干个数据项组成。(如花名册,每个元素除了学生的学号之外,还有同学的姓名,性别,出生年月等都是数据项)数据的类型要相同。
线性表的抽象数据类型
线性表重置为空表。
线性表的顺序存储结构
线性表的两种物理结构:
第一种:顺序存储结构
是指用一段地址连续的存储单元依次存储线性表的数据元素。
顺序存储方式:可以用c语言的一维数组来实现顺序存储结构,即把第一个数据元素存到数组下标为0的位置中,接着把线性表相邻的元素存储在数组中相邻的位置。
线性表的顺序存储的结构代码
#define MAX 20 //存储空间初始分配量
typedef int A; //A类型根据实际情况而定,这里假设为int
typedef struct
{
A data[MAX];//数组存储数据元素,最大值为MAX
int length;//线性表当前长度
}SqList;描述顺序存储结构需要三个属性:
1.存储空间的起始位置:数组 data,它的存储位置就是存储空间的存储位置。
2.线性表的最大存储容量:数组长度 Max。
3.线性表的当前长度:length。
数据长度与线性表长度区别
数组的长度和线性表的长度有区别
数组的长度是存放线性表的存储空间的长度,存储分配后这个量是一般是不变的。
线性表的长度是线性表中数据元素的个数,随着线性表插入和删除操作的进行,这个量是变化的。在任意时刻,线性表的长度应该小于等于数组的长度。
地址计算方法
线性表的定义起始也是1,可C语言中的数组却是从0开始第一个下标的,于是线性表的第i个元素是要存储在数组下标为 i-1 的位置,即数据元素的序号和存放它的数组下标之间存在对应关系。
注意:用数组存储顺序表意味着要分配固定长度的数组空间,由于线性表中可以进行插入和删除操作,因此分配的数组空间要大于等于当前线性表的长度。
内存中的地址都是有编号的。存储器中的每个存储单元都有自己的编号,这个编号称为地址。
由于每个数据元素,不管它是整型、实型还是字符型,它都是需要占用一定的存储单元空间的。假设占用的是c个存储单元,那么线性表中第i+1个数据元素的存储位置和第i个数据元素的存储位置满足下列关系(L0C表示获得存储位置的函数)。
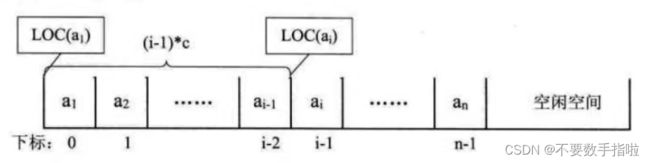
所以对于第i个数据元素 ai的存储位置可以由a1推算得出:
通过这个公式,可以随时算出线性表中任意位置的地址,不管它是第一个还是最后一个,都是相同的时间。那么我们对每个线性表位置的存入或者取出数据,对于计算机来说都是相等的时间,也就是一个常数,因此用我们算法中学到的时间复杂度的概念来说,它的存取时间性能为 0(1)。我们通常把具有这一特点的存储结构称为随机存取结构。
顺序存储结构的插入与删除
获得元素操作:
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
typedef int Status;//Status是函数的类型,其值是函数结果状态代码,如OK等
//初始条件:顺序线性表L已经存在,1<=i<=ListLength(L)
//操作结果:用e返回L中第i个数据元素的值
Status GetElem(SqList L, int i, ElemType* e)
{
if (L.length == 0 || i<1 || i>L.length)
return ERROR;
*e = L.data[i - 1];
return OK;
}返回类型Status是一个整型,返回OK代表1,ERROR代表0。
插入操作 :
时间复杂度为O(1)。
在线性表L中的第i个位置插入新元素e.
插入算法的思路:
1.如果插入位置不合理,抛出异常;
2.如果线性表长度大于等于数组长度,则抛出异常或动态增加容量;
3.从最后一个元素开始向前遍历到第i个位置,分别将它们都向后移动一个位置;
4.将要插入元素填入位置i处;
5.表长加1。
实现代码如下:
//初始条件:顺序线性表L已存在,1<=i<=ListLength(L),
//操作结果:在L中第i个位置之前插入新的数据元素e,L的长度加1
Status ListInsert(SqList* L, int i, ElemType e)
{
int k;
if (L->length == MAXSIZE)//顺序线性表已经满
return ERROR;
if (i<1 || i>L->length + 1)//当i不在范围内时
return ERROR;
if (i <= L->length)//若插入数据位置不在表尾
{
for (k = L->length - 1; k >= i - 1; k--) {//将要插入位置后数据元素向后移动一位
L->data[k + 1] = L->data[k];
}
L->data[i - 1] = e;//将新元素插入
L->length++;
return 0;
}
}删除操作:
删除算法的思路:
抛出异常如果删除位置不合理,
取出删除元素;
从删除元素位置开始遍历到最后一个元素位置,分别将它们都向前移动一个位置;
表长减1。
代码的实现如下:
//初始条件:顺序线性表L已存在,1<=i<=ListLength(L),
//操作结果:删除L的第i个数据元素,并用e返回其值,L的长度减一
Status ListDelete(SqList* L, int i, ElemType* e)
{
int k;
if (L->length == 0)//线性表为空
return ERROR;
if (i<1 || i>L->length)//删除位置不正确
return ERROR;
*e = L->data[i - 1];
if (i < L->length)//如果删除不是最后位置
{
for (k = 1; k < L->length; k++) //将删除位置后继元素前移
L->data[k - 1] = L->data[k];
}
L->length--;
return OK;
}平均时间复杂度还是O(n)。
线性表顺序存储结构的优缺点
优:无须为表示表中元素之间的逻辑关系而增加额外的存储空间
可以快速地存取表中任一位置的元素
缺:插入和删除操作需要移动大量元素
当线性表长度变化较大时,难以确定存储空间的容量
造成存储空间的“碎片"