二叉树的初步学习（初学萌新之人所写）

问题

1.二叉树是什么？

2.我们为什么要学习二叉树，他的优点是什么？

3.如何构建最小堆？

4.如何实现堆排序

二叉树是什么？

二叉树顾名思义，它很像一棵树，有着许多的节点，每个节点都指向下两个节点，就像一颗树倒过来的样子。其中二叉树分为两种类型，第一是满二叉树，第二是完全二叉树。

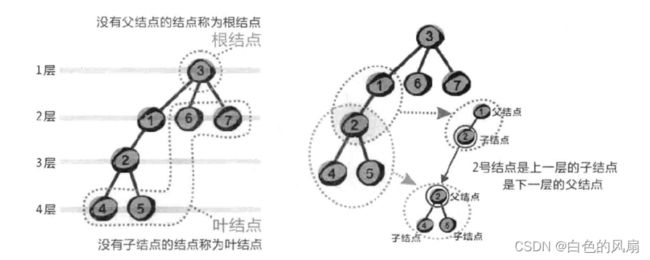
满二叉树如图所示（该图来自《啊哈！算法》）

可以看到这个树十分的饱满，没有说少了或者多了，每个节点就是对应着两个节点（除了最后一行，这个最后一行也被称为“叶节点”）， 看一下上图，以数值为2的节点为标准，它上面的就被称为父节点（我还是习惯叫它爹），它下面的叫做子节点。而最后一行没有子节点的就叫做叶节点。

没有父节点的节点叫做根节点。如上图值为1的点就叫做根节点。

该图来自《啊哈！算法》

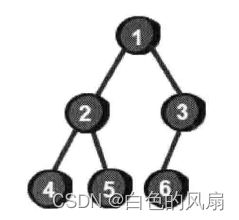
完全二叉树（该图来自《啊哈！算法》）（就是没有满二叉树那么饱满，且只有左边的有缺失）

 

 有着二叉树的模样，且父节点始终比子节点要小的二叉树就叫做最小堆，如果所有父节点都要比子节点要大，则我们则叫最大堆

我们为什么要学习二叉树，他的优点是什么？

就我目前的学习进度来说，他的有点就一个字---快！

来一个案例（虽然我只学了这一个案例）
找到最小值，最基本的思路就是用一个for循环来遍历整个数组，然后用一个变量min来记录这个最小值，如果我们将这个最小的数删掉，然后插入一个新的数，直到将这个数组全部替换完，如果是这样的，那么时间复杂度就是O(n*n)。
如果在我们存入数组的时候就将存入的树按照二叉树的形式进行存储，那么按照之前所说的父节点要比子节点要小的这个性质，那最上面那个数（最开始的那个父节点），是不是就是最小值了？
  而且就算是找也是像折半查找一样，每次进行查找的时候都是在一种情况下进行的查找（换言之就是在每一层中的一个分支进行的查找），所以就要比每次遍历每个数要来的快。

如何构建最小堆？

在这里我就需要一个下调的函数，为了使父节点比子节点要小，给它命名为void siftdown(int i)

代码如下（解释在代码里面）

void siftdown(int i)//变量为下标
{
	int t,flag=0;
	while(i*2<=n&&flag==0)
	{
		if(h[i]>h[i*2])//判断左儿子和爹的关系，如果爹大于左儿子，那么爹就需要向下移动
		{
			t=2*i;//t用于记录较小值
		}
		else
		{
			t=i;
		}
		if(i*2<=n)//如果有右儿子
		{
			if(h[t]>h[2*i+1])
			t=2*i+1;
		}
		if(t!=i)//如果发现这个最小值不是爹，就说明有更小的值存在（这个最小值的编号存放在t中）
		{
			swap(i,t);//交换函数，待会后面会进行补充
			i=t;
		}
		else//如果爹发现自己是最小的值，那就可以跳出循环了
		flag=1;
	}	
	return ;
}

 交换函数

void swap(int x,int y)//数组要作为全局变量进行使用
{
int tmp=h[x];
h[x]=h[y];
h[y]=h[x];
return ;
}

为了方便在实现最小堆，我们需要一个上升的函数，将较小的数从二叉树的叶节点升上来（这个是从头开始）
代码如下

void siftup(int i)
{
	int flag=0;//还是需要一个标记来判断
	if(i==1)return ;//说明已经到了根节点了
	while(flag==0&&i>1)//由于上升是单向上升，所以就没有左儿子和右儿子这一说法
	{
		if(h[i]

 还有一种更快的方式：首先我们需要知道完全二叉树的一个性质，就是最后一个非叶节点的编号是n/2。由于叶节点没有子节点，所以我们不需要对叶节点进行处理，然后最后一个非叶节点的编号是n/2，所以我们从n/2开始知道编号为1，进行siftdown函数（因为如果不用数的下降，就波及不到叶节点）。

实现这个操作叶很简单

for(int i=n/2;i>=1;i--)
{
	siftdown(i);
}

 如何实现堆排序

我们通过前面的学习可以知道，建立好的最小堆的根节点就是这个数组里面的最小值，所以我们每次只要将堆的根节点输入到一个全新的数组中然后再将根节点删除然后再使用siftdown()函数就可以把堆的下一个次小值给输入到这个全新的数组中，以次类推。这样就可以得到从小到大的数组。

int deletemin()
{
int t=h[1];
h[1]=h[n];
n--;//出堆，这个的原理就有点像出栈
siftdown(1);//调用下移函数，使其重新调一个最小值上来
return t;//打印最小值最小值
}

最后只需要将全部这些构造好的函数组合在一起，堆排序就实现了。

#include
int n=0;
int h[100];
void swap(int x,int y)
{
	int tmp=h[x];
	h[x]=h[y];
	h[y]=tmp;
}
void siftdown(int i)
{
	int t,flag=0;
	while(2*i<=n&&flag==0)
	{
		if(h[i]>h[2*i])
			t=i*2;
		else
			t=i*2;
		if(2*i+1<=n)
		{
			if(h[2*i+1]1)//由于上升是单向上升，所以就没有左儿子和右儿子这一说法
	{
		if(h[i]