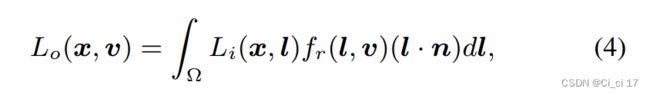【反渲染高斯】GS-IR: 3D Gaussian Splatting for Inverse Rendering

概要

会有自己的理解PS，不保证正确，欢迎评论中指出错误。
我们提出了一种基于3D高斯溅射(GS)的新型反向渲染方法GS-IR，它利用前向映射体渲染forward mapping volume rendering来实现逼真的新视图合成和重照明结果。与先前使用隐式神经表征和体绘制(例如NeRF)的工作不同，这些工作具有低表达能力和高计算复杂性，我们扩展了GS，这是一种用于新视图合成的高性能表征，可以从未知光照条件下捕获的多视图图像中估计场景几何、表面材料和环境照明。将GS引入到反向渲染中存在两个主要问题:
1)GS不支持生成可信的原生法线
;2)前向映射(如栅格化和飞溅)不能像后向映射(如光线追踪)那样跟踪遮挡。为了解决这些挑战，我们的GS-IR提出了一种有效的优化方案，该方案结合了基于深度衍生的正则化法用于正态估计和基于烘烤的遮挡法来模拟间接照明depth-derivationbased regularization。灵活和富有表现力的GS表示使我们能够实现快速和紧凑的几何重建，逼真的新视图合成和有效的基于物理的渲染。
PS: 前向映射：是三维物体投影到画布上
后向映射是下图image plane 发射射线，确定射线的颜色

我们通过对各种具有挑战性的场景进行定性和定量评估，证明了我们的方法优于基线方法。源代码可从https://github.com/lzhnb/GS-IR获得。

intro

反向渲染是一项由来已久的任务，旨在回答以下问题： "（如如何从多视角图像中推导出三维场景的物理属性（如几何、材质和照明）？

这个问题本身就具有挑战性和不确定性，尤其是当输入图像是在光照未知的不可控环境中捕获的时候。最近的研究[9, 10, 33, 44]试图通过采用类似于 NeRF [27] 的隐式神经表征（利用多层感知器 (MLP)）来解决这一问题。然而，目前采用 MLP 的方法面临着表达能力低和计算需求高的挑战，这极大地限制了反向渲染的效果和效率，尤其是在无法以交互速率 interactive rates进行渲染的情况下。三维高斯拼接（GS）[23] 是最近出现的一种很有前途的技术，它可以对三维静态场景进行建模，并将渲染速度大大提高到实时水平。它使场景表示更加紧凑，
PS：紧凑可能是相对于点云，gs有体积能够一个贴着一个，空隙小？
并为新颖的视图合成实现了快速和顶级性能。将其引入反渲染流水线是自然和必要的，包括几何重建、材料分解和光照估计。

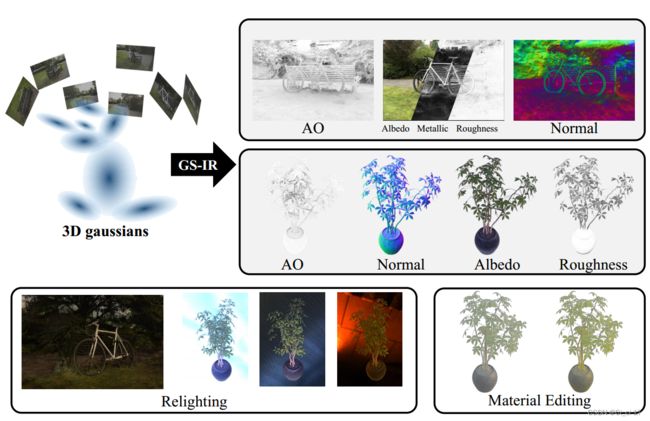
鉴于复杂场景的多视图捕获图像，我们提出了GS-IR (3D高斯溅射反演渲染)，它利用3D高斯和前向映射溅射来恢复高质量的物理属性(例如，法线，材料，照明)。这使我们能够执行重照明和材料编辑，从而产生出色的反向渲染结果。放大后的屏幕观看效果更好，尤其是自行车车轴的材料分解和正常重建效果显著。

不像nerf里的光线追踪，高斯模型在稀疏点周围生成一组三维高斯。在高斯优化过程中**，高斯密度的自适应控制可能会导致几何结构松散**，从而难以准确估计场景的法线。因此，有必要引入一种精心设计的策略来规范 GS 的法线估算。我们的目标是使用三维高斯作为场景表示，对未知光照条件下捕获的多视角图像进行反渲染。然而，在自然光照条件下捕捉观测结果往往会产生复杂的效果，如柔和的阴影和相互反射。TensoIR [21] 利用 NeRF 的光线追踪技术直接为遮挡和间接光照建模。相比之下，3D GS 用可微分前向映射体积渲染取代了 NeRF 中的光线追踪，直接将 3D 高斯投射到 2D 平面上。这种策略提高了渲染效率，但却难以计算遮挡。受实时渲染中使用的 “间接照明缓存”[4] 的启发，我们尝试将==遮挡烘焙到体积中进行缓存==。在本文中，我们提出了一种新颖的基于三维高斯的反渲染框架，称为 GS-IR（三维高斯拼接反渲染），它利用前向映射拼接来推断复杂场景的物理属性。据我们所知，我们的方法是首个将 GS 技术引入反渲染的工作，它可以同时估算场景几何、材质、颜色、色彩、颜色和颜色的物理属性。
PS：
在计算机图形学和三维图形领域，“bake” 一词通常指的是将高级别的信息（例如光照、纹理、阴影）转换为纹理贴图或其他形式的数据，以便在渲染过程中更高效地使用。
“Baking” 过程的目的是为了减轻实时渲染引擎的计算负担，特别是在游戏开发中。通过在预处理阶段计算并存储某些效果，可以在运行时更迅速地呈现图形。例如，光照贴图可以在烘焙时计算，然后在实时渲染中使用，避免了每帧都重新计算光照的开销

• 我们提出的 GS-IR 可将场景建模为一组三维高斯，从而实现基于物理的渲染，并为物体和场景提供最先进的分解结果；
• 我们提出了一种高效的正则化优化方案，可将深度梯度集中在 GS 周围，并为 GS-IR 生成可靠的法线；-
• 我们开发了一种嵌入 GS-IR 的基于烘焙的方法，以处理间接照明建模中的遮挡问题；

总结

鉴于复杂场景的多视角捕捉图像，我们提出了 GS-IR（用于反渲染的三维高斯拼接），它利用三维高斯和前向映射拼接来恢复高质量的物理属性（如法线、材质、光照）。这使我们能够执行重新照明和材质编辑，从而获得出色的反渲染效果。在屏幕上放大观看效果更佳，尤其是自行车车轴的出色材质分解和法线重建。
我们提出的 GS-IR 是一种基于三维高斯拼接（GS）的新型反渲染方法，它采用前向映射体积渲染来实现逼真的新型视图合成和重新照明效果。具体来说，我们的 GS-IR 提出了一种高效的优化方案，该方案采用**基于深度衍生的正则化来进行法线估算，并采用基于烘焙的遮挡来模拟间接照明**。这些组件最终被用于分解材料和照明。我们的大量实验证明，GS-IR 能有效实现最先进的反向渲染效果，在重建质量和效率方面都超越了以前的神经方法。

相关工作

Inverse Rendering

反渲染的目的是将图像的外观分解为几何形状、材料属性和照明条件。考虑到观察到的图像与底层场景属性之间固有的模糊性，许多方法被提出，并采用了不同的限制设置，如用固定照明和旋转物体捕捉图像 [16, 36]，用移动相机和同位照明捕捉图像 [7, 8, 26, 30]。结合神经表征，反渲染模拟场景，模拟光线如何与具有不同材料属性的神经体相互作用，并在优化过程中估计照明和材料参数[6、9、10、19、21、33、40、42、44、45]。神经反射场[6]假定有一个已知的点光源，并将场景表示为一个由体积密度、表面法线和双向反射分布函数（BRDF）组成的场，其中有一个反弹直射照明bounce direct illumination。NeRV [33] 和 InvRender [45] 扩展到任意已知照明条件，并训练额外的 MLP 来模拟光的可见性。PhySG [40] 假设光源完全可见，不进行阴影模拟，并用球形高斯表示照明和场景 BRDF，以加快速度。TensoIR [21] 采用高效的 TensoRF [14] 表示法，可通过光线追踪计算可见度和间接照明，但仅限于对象级。在这项工作中，我们提出了一种基于 GS 的管道，用于恢复几何图形、材质和光照。

pre

在本节中，我们将提供技术背景和数学符号，这些都是在后续章节中介绍我们所建议的方法所必需的。

3D高斯飞溅(3D Gaussian splplatting, GS)[23]是一种以点云形式的显式3D场景表示。每个点都用高斯函数g表示，它近似于钟形曲线的形状，定义为:

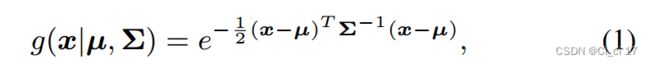
其中，µ∈R 3为其均值向量，Σ∈R 3×3为各向异性协方差矩阵。将三维高斯函数的平均向量µ参数化为µ=(µx，µy，µz)，协方差矩阵Σ分解为缩放矩阵S和旋转矩阵R Σ = RSS^TR^T。S和R表示对角矩阵diag(sx, sy, sz)和由单位四元数q构成的旋转矩阵。给定一个具有外在矩阵T和内在矩阵K的观看变换，则从三维点x到二维像素u的平均向量µ和协方差矩阵Σ’定义为:

其中J是透视投影的仿射近似的雅可比矩阵。此外，每个高斯函数通过一组球面谐波(SH)系数表示与视图相关的颜色ci，然后乘以不透明度α进行体渲染。最后根据Eq.(1)和Eq.(2)得到像素u处的颜色C.

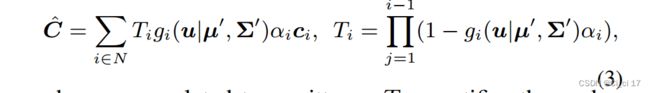
其中累计透射率Ti量化了像素u处第i次高斯的概率密度。

在GS-IR中，我们利用经典的渲染方程来制定表面点x的法向n的出射亮度:

Ω为以x为中心的上半球，l和v分别为入射方向和观察方向。Li(x,l)表示从l处接收到x处的辐射。值得注意的是，我们遵循==Cook-Torrance microfacet==模型[15,35]，并将双向反射分布函数(BRDF) fr表示为**反照率a∈[0,1]3，金属m∈[0,1]，粗糙度ρ∈[0,1]**的函数:

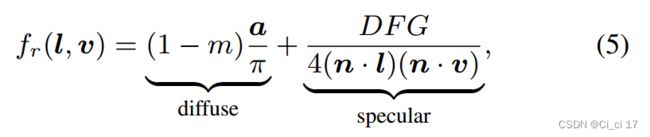
其中，微面分布函数D、菲涅耳反射F和几何阴影因子G与表面粗糙度ρ有关。我们使用三维高斯函数在GS-IR中存储这些材料属性。

Method

给定一组经过校准的RGB图像$\{I_m{\}}_m^M=1$的目标场景，在静态的，但未知的照明下，反向渲染旨在分解场景的内在属性，包括法线，材料和照明。这种分解有助于目标场景的恢复和后续版本。由于GS在质量和速度上的卓越表现[23]，我们提出了一个由三个精心设计的阶段策略组成的新框架GS- IR，如图2所示。

在初始阶段，我们利用可微喷溅来优化三维高斯。同时，我们利用从渲染深度图派生的梯度来监督存储在三维高斯曲线中的法线(参见4.1。)。在第二阶段，我们根据学习到的几何信息(即深度和法线)预先计算遮挡，并将其存储在一个高效的基于球面谐波的架构中，以模拟间接照明(参见4.2。)。在最后阶段，我们将可微分喷溅与基于物理的渲染(PBR)管道相结合，以优化照明和材料感知的3D高斯(参见。4.3秒。)。

GS-IR 管道。我们提出了一种新颖的基于高斯的反渲染框架，称为 GS-IR，用于从多视角捕捉的图像中重建场景几何、材质和未知的自然光照。我们的 GS-IR 包括三个精心设计的阶段策略，使用三维高斯和可微分前向映射拼接来实现基于物理的渲染。在我们的方法中，高斯不仅存储了基本的 GS 信息，还存储了法线和材料属性，从而增强了反渲染任务的能力。

nomal的重建

在初始阶段，我们优化了三维高斯函数，用于从观测图像中重建几何形状，记为G。

优化后的G函数作为曲面点及其对应法线n的几何代理，这对于成功的逆绘制至关重要。正如第1节所强调的，在基于gs的框架内生成合理的法线是一项重大挑战。为了解决这个问题，我们引入了一种直观的策略来提高深度D，并利用深度梯度来推导伪法线 n ^ D ^ = ∇ u v D ^ \hat{n}_{\hat{D} } =∇_{uv}\hat{D}