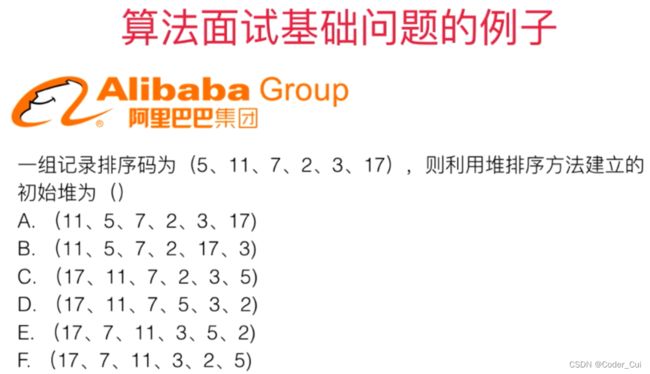
《玩儿转算法面试》学习笔记

1. 算法面试到底是什么鬼

重在思路 ：

 注意：Java排序底层算法就是三路快排

 

 

 

2. 面试中的复杂度分析

2.1 时间复杂度

       一个操作如果和样本的数据量没有关系，每次都是在固定时间内完成操作，那么这个操作叫做常数操作，例如：+、-、*、\、位运算等。

       时间复杂度可以看作是一个在算法流程中用来衡量常数操作数量的指标，常用O来表示，读作Big O。具体来说，先要对一个算法流程非常熟悉，然后去写出这个算法流程中发生了多少次常数操作，进而总结出常数操作数量的表达式。

       在进行算法分析时，一般用n表示数据规模，用T(n)表示语句总的执行次数，它是关于问题规模n的函数，要分析出T(n)随n如何变化，才能确定T(n)的数量级。算法的时间复杂度即算法的时间量度，记作T(n)=O(f(n))，表示随着数据规模n的增大，算法执行时间的增长率和f(n)的增长率相同，记作算法的渐进时间复杂度或时间复杂度，其中，f(n)是关于数据规模n的一个函数。用O()来表示算法的时间复杂度，一般情况下，随着n的增大，T(n)增长最慢的算法就是最优算法。对于数据规模n的理解如下：

如果要想在1s之间解决问题：

• O(n^2) 的算法可以处理大约10^4级别的数据

• O(n) 的算法可以处理大约10^8级别的数据

• O(nlogn) 的算法可以处理大约10^7级别的数据

根据执行次数T(n)或常数操作数量推导O表达式时，要注意以下几条原则：

• 用常数1取代运行时间中的所有加法常数；

• 在修改后的运行次数函数中，只保留最高阶项，不要低阶项；

• 如果最高阶项存在且其系数不是1，则去除与这个项相乘的系数。

  剩下的部分如果为f(n)，则时间复杂度为O(f(n))。

举例：

• 二分查找法：O(logn） 所需执行指令数：a*logn

• 寻找数组中最大/最小值：O(n) 所需执行指令数：b*n

• 归并排序算法：O(nlogn） 所需执行指令数：c*nlogn

• 选择排序算法：O(n^2) 所需执行指令数：d*n^2

常见的时间复杂度所耗费的时间从小到大依次是：

O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)

       在学术界，严格来讲，O(f(n))表示算法执行的上界，对于归并排序算法的时间复杂度可以说是O(nlogn)的，也可以说是O(n^2)的。对算法的分析，—种方法是计算所有情况的平均值，这种时间复杂度的计算方法称为平均时间复杂度；另一种方法是计算最坏情况下的时间复杂度，这种方法称为最坏时间复杂度。一般在没有特殊说明的情况下，都是指算法的最坏情况下的时间复杂度。但是在业界，通常使用O来表示算法执行的最低上界，一般不会说归并排序是O(n^2)的。

       评价一个算法流程的好坏，要先看时间复杂度的指标，然后再分析不同数据样本下的实际运行时间，即“常数项时间”。

注意：不是有递归的函数就一定是O(nlogn)。

• 如果递归函数中，只进行一次递归调用，递归深度为depth；
• 在每个递归函数中，时间复杂度为T，则总体的时间复杂度为O(T*depth)。

2.2 空间复杂度

即所需要额外占用内存空间的大小，例如：

• 多开一个辅助的数组：O(n）

• 多开一个辅助的二维数组：O(n^2）

• 多开常数空间：O(1)

• ......

注意：递归调用是有空间代价的。

 // 空间复杂度O(1)
 public int sum(int n){
     int ret = 0;
     for(int i=0;i<=n;i++){
         ret+=i;
     }
     return ret;
 }
 ​
 // 空间复杂度O(1)
 public void swap(int a,int b){
     int temp = a;
     a = b;
     b = temp;
 }
 ​
 // 空间复杂度O(n)
 public int sum2(int n){
     if(n==0){
         return 0;
     }
     return n+sum2(n-1);
 }
 ......

3. 数组相关问题

排序：选择排序；插入排序；归并排序；快速排序

查找：二分查找法

数据结构：栈、队列、堆

......

3.1 二分查找法(BinarySearch)

       二分查找法的思想是在1946年提出的，但是第一个没有bug的二分查找法是在1962年才出现的。对于有序数列，才能使用二分查找法，实现要对序列排好序。

Java代码实现：

• 数组工具类：ArrayUtil

 package array;
 ​
 /**
  * @ClassName ArrayUtil
  * @Description 用来生成指定长度、指定范围的随机数组或有序数组
  * @Author Jiangnan Cui
  * @Date 2022/10/23 11:47
  * @Version 1.0
  */
 public class ArrayUtil {
     // 私有构造方法
     private ArrayUtil(){};
 ​
     /**
      * @MethodName generateRandomArray
      * @Description 产生指定长度、指定范围的随机数组
      * @param: n 数组长度
      * @param: rangeL 范围最小值
      * @param: rangeR  范围最大值
      * @return: java.lang.Integer[]
      * @Author Jiangnan Cui
      * @Date 17:54 2022/10/23
      */
     public static Integer[] generateRandomArray(int n,int rangeL,int rangeR){
         // 前提条件
         assert n > 0 && rangeL <= rangeR;
         // 声明数组
         Integer[] arr = new Integer[n];
         // 数组赋值
         for(int i = 0;i < n; i++){
             // 生产rangeL到rangeR之间的随机整数
             arr[i] = (int)(Math.random()*(rangeR-rangeL+1)) + rangeL;
         }
         return arr;
     }
 ​
     /**
      * @MethodName generateOrderArray
      * @Description 产生指定长度的有序数组
      * @param: n 数组长度
      * @return: java.lang.Integer[]
      * @Author Jiangnan Cui
      * @Date 17:55 2022/10/23
      */
     public static Integer[] generateOrderArray(int n){
         // 前提条件
         assert n>0;
         // 声明数组
         Integer[] arr = new Integer[n];
         // 数组赋值
         for(int i=0;i 
  
 
   
 
二分查找法具体实现
 
 
  
 
  
 package array;
 /**
  * @ClassName BinarySearch
  * @Description 二分查找测试
  * @Author Jiangnan Cui
  * @Date 2022/10/23 17:47
  * @Version 1.0
  */
 public class BinarySearch {
     /**
      * 无参构造
      */
     private BinarySearch(){}
 ​
     /**
      * @MethodName binarySearch
      * @Description 二分查找实现代码：在[0,n-1]范围内进行查找
      * @param: arr 目标数组
      * @param: n 数组长度
      * @param: target 目标元素
      * @return: int
      * @Author Jiangnan Cui
      * @Date 17:59 2022/10/23
      */
     public static int binarySearch(Integer[] arr, int n, int target){
         // 定义查找左右边界，在[left,...,right]的范围内寻找target
         int left = 0, right = n - 1;// 即数组的开始下标0、结束索引arr.length-1
         // 事先不明确循环次数时，使用while循环，循环条件：left<=right
         // 特别注意：当left==right时，区间[left,...,right]依然有效，此时只含有一个元素，，所以能取==
         while(left <= right){
             // 取中点，考虑到left+right可能会出现整型溢出问题，修改如下，注意位运算速度更快
             int mid = left + ((right - left) >> 2);// <<：左移，相当于乘法，增大倍数；>>：右移，相当于除法，缩小倍数
             // 如果目标值等于中间值，直接返回数组下标即可
             if(arr[mid] == target){
                 return mid;
             }else if(arr[mid] < target){// 如果目标值大于中间值，说明需要向右查找，修改左边界，右边界不变
                 left = mid + 1;// 注意此时不包含mid
             }else{// 如果目标值小于中间值，说明需要向左查找，左边界不变，修改右边界
                 right = mid - 1;// 注意此时不包含mid
             }
         }
         // 跳出循环时，说明没有满足条件的元素，直接返回-1
         return -1;
     }
 ​
     /**
      * @MethodName binarySearch2
      * @Description 分查找实现代码：在[0,n)范围内进行查找
      * @param: arr 目标数组
      * @param: n 数组长度
      * @param: target 目标元素
      * @return: int
      * @Author Jiangnan Cui
      * @Date 18:14 2022/10/23
      */
     public static int binarySearch2(Integer[] arr,int n,int target){
         // 定义查找左右边界，在[left,...,right)的范围内寻找target
         int left = 0,right = n;// 即数组的开始下标0、数组长度arr.length，此时数组下标不能取n
         // 事先不明确循环次数时，使用while循环，循环条件：left> 2);// <<：左移，相当于乘法，增大倍数；>>：右移，相当于除法，缩小倍数
             // 如果目标值等于中间值，直接返回数组下标即可
             if(arr[mid] == target){
                 return mid;
             }else if(arr[mid] < target){// 如果目标值大于中间值，说明需要向右查找，修改左边界，右边界不变
                 left = mid + 1;// 注意此时不包含mid
             }else{// 如果目标值小于中间值，说明需要向左查找，左边界不变，修改右边界
                 right = mid;// 注意此时不包含mid，又由于右边界取不到，为了得到mid-1，此处需要取mid
             }
         }
         // 跳出循环时，说明没有满足条件的元素，直接返回-1
         return -1;
     }
 ​
     // 测试代码
     public static void main(String[] args) {
         // 生成随机数组
         int n = (int)Math.pow(10,7);
         Integer[] data = ArrayUtil.generateOrderArray(n);
         // 开始时间
         long startTime = System.currentTimeMillis();
         for (int i = 0; i < n; i++) {
             if(i!=binarySearch2(data,n,i)){
                 throw new IllegalStateException("find i failed!");
             }
         }
         // 结束时间
         long endTime = System.currentTimeMillis();
         System.out.println("BinarySearch test complete.");
         System.out.println("Test cost:"+(endTime-startTime)+"ms");
     }
 }
 
  
输出结果：
 
  
 BinarySearch test complete.
 Test cost:442ms
 
  
 
  
如何写出正确的程序？
 
  
 
   
 
明确变量的含义
 
 
  
 
  
 
   
 
注意循环不变量
 
 
  
 
  
 
   
 
小数据量调试（自己举例实际调试）
 
 
  
 
  
 
   
 
大数据量测试
 
 
  
 
  
 
  
 
  
3.2 面试问题实战
 
  
3.2.1 283. 移动零
 
  
 
  
 
  
对应博客题目实现代码：LeetCode 283. 移动0_Coder_Cui的博客-CSDN博客
 
  
 
  
3.2.2 27. 移除元素
 
  
​
 
  
 
  
要考虑的因素：
 
  
 
   
 
如何定义删除？从数组中删除，还是放在数组末尾？
 
 
  
 
  
 
   
 
剩余元素的排列是否要保证原有的相对顺序？
 
 
  
 
  
 
   
 
是否有空间复杂度的要求？O(1)
 
 
  
 
  
对应博客题目实现代码：LeetCode 27.移出元素_Coder_Cui的博客-CSDN博客
 
  
 
  
3.2.3 26. 删除有序数组中的重复项
 
  
​
 
  
对应博客题目实现代码：LeetCode 26. 删除有序数组中的重复项_Coder_Cui的博客-CSDN博客
 
  
 
  
3.2.4 80. 删除有序数组中的重复项 II
 
  
 
  
​
 
  
对应博客题目实现代码：LeetCode 80. 删除有序数组中的重复项 II_Coder_Cui的博客-CSDN博客
 
  
 
  
 
  
3.3 基础算法思路的应用
 
  
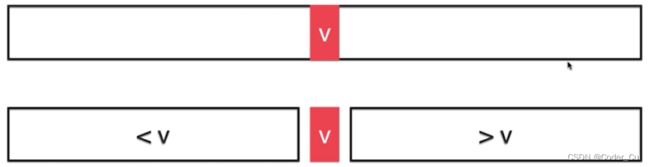
---三路快排
 
  
3.3.1 75. 颜色分类
 
  
 
  
 
  
计数排序：适用于元素个数非常有限的情况下。
 
  
针对此题只需要分别统计出0、1、2的元素个数，放回原有的位置即可。
 
  
对应博客题目实现代码：LeetCode 75. 颜色分类_Coder_Cui的博客-CSDN博客
 
  
 
  
3.3.2 88. 合并两个有序数组
 
  
 
  
 
  
对应博客题目实现代码：LeetCode 88. 合并两个有序数组_Coder_Cui的博客-CSDN博客
 
  
 
  
3.3.3 215. 数组中的第K个最大元素
 
  
 
  
 
  
 
  
 
  
对应博客题目实现代码：
 
  
待完善。。。。。。
 
  
 
  
 
  
 
  
下一次视频内容：3-6 对撞指针 Two Sum II - Input Array is Sorted
 
  
 
  
 
  
 
  
4. 查找表相关问题
 
  
待完善。。。
 
  
 
  
 
  
5. 在链表中穿针引线
 
  
待完善。。。
 
  
 
  
 
  
6. 栈，队列，优先队列
 
  
待完善。。。
 
  
 
  
 
  
7. 二叉树和递归
 
  
待完善。。。
 
  
 
  
 
  
8. 递归和回溯法
 
  
待完善。。。
 
  
 
  
 
  
9. 动态规划基础
 
  
待完善。。。
 
  
 
  
 
  
10. 贪心算法
 
  
待完善。。。
 
  
 
  
 
  
11. 课程结语
 
  
待完善。。。