剑指Offer：重建二叉树

描述

给定节点数为 n 的二叉树的前序遍历和中序遍历结果，请重建出该二叉树并返回它的头结点。
例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建出如下图所示。

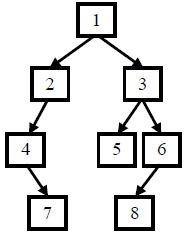
提示:
1.vin.length == pre.length
2.pre 和 vin 均无重复元素
3.vin出现的元素均出现在 pre里
4.只需要返回根结点，系统会自动输出整颗树做答案对比
数据范围：n \le 2000n≤2000，节点的值 -10000 \le val \le 10000−10000≤val≤10000
要求：空间复杂度 O(n)，时间复杂度 O(n)

我的思路

我记得我以前写过一次这个题，就是写到一半跑路了，搞不明白，今天一定要搞明白。
这道题是给出前序遍历和中序遍历，很痛苦的是我只能根据手算得出来。算了，拿例子分析一下看看能不能分析出个什么规律。

前序遍历序列{1,2,4,7,3,5,6,8}
中序遍历序列{4,7,2,1,5,3,8,6}

拿到前序和中序在判断的时候首先要想到，因为前序遍历是中左右，中序遍历是左中右，这时我们就可以根据前序的第一位判断节点的分布，显然这个元素1是整个树的根节点。所以可能需要一个辅助队列来按照层序遍历的顺序进行排序。这时1先入队，判断哪个是1的左子树和右子树，这时中序遍历1之前的元素都得弹出，我们把以2为根节点作为一个一颗子树，依然不能得出2的左右子树分别是哪个，那就以4为根节点，7一定是4的右子树，因为中序遍历中4在7前面，这时回溯看上一层以2为根节点这层，4一定是2的子树，但是是左子树还是右子树呢？显然是左子树，因为如果是右子树的话中序遍历中7就会在4前面，所以一开始就可以判定4是某个树的左子树，这时左边排序完了。
那代码怎么实现呢？我也不知道，看着先想想，感觉是用递归的，那递归的返回值结束条件判断逻辑是什么？每次递归一开始都会存储一个节点作为本次的根节点，递归的参数应该是有一个int类型的根节点信息作为root。不行，整不明白，溜了，去看别人的题解。

别人的思路

这里借鉴的是K神的思路

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    HashMap<Integer, Integer> map = new HashMap<>();//标记中序遍历
    int[] preorder;//保留的先序遍历，方便递归时依据索引查看先序遍历的值

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        this.preorder = preorder;
        //将中序遍历的值及索引放在map中，方便递归时获取左子树与右子树的数量及其根的索引
        for (int i = 0; i < inorder.length; i++) {
            map.put(inorder[i], i);
        }
        //三个索引分别为
        //当前根的的索引
        //递归树的左边界，即数组左边界
        //递归树的右边界，即数组右边界
        return recur(0,0,inorder.length-1);
    }

    TreeNode recur(int pre_root, int in_left, int in_right){
        if(in_left > in_right) return null;// 相等的话就是自己
        TreeNode root = new TreeNode(preorder[pre_root]);//获取root节点
        int idx = map.get(preorder[pre_root]);//获取在中序遍历中根节点所在索引，以方便获取左子树的数量
        //左子树的根的索引为先序中的根节点+1 
        //递归左子树的左边界为原来的中序in_left
        //递归左子树的右边界为中序中的根节点索引-1
        root.left = recur(pre_root+1, in_left, idx-1);
        //右子树的根的索引为先序中的 当前根位置 + 左子树的数量 + 1
        //递归右子树的左边界为中序中当前根节点+1
        //递归右子树的右边界为中序中原来右子树的边界
        root.right = recur(pre_root + (idx - in_left) + 1, idx+1, in_right);
        return root;

    }

}

确实是很神，我一开始一直在想怎么处理中序数组的问题，因为前序数组可以直接放在那，每下一个元素都可以是根节点的值，但是中序数组的值并不行。果然是使用了递归解决，二叉树大多都用递归，这也是很好想的了，就是实现细节有点困难。
在递归的逻辑里，取前序数组第一位数作为根节点很好理解。

int idx = map.get(preorder[pre_root]);
//获取在中序遍历中根节点所在索引，以方便获取左子树的数量

这一步是我觉得很神的一步，我想不出来用哈希表存储中序数组并且将value设置为下标索引值，其实另一个代码写的更明白

for (int i = 0; i < preorder.length; i++) {
            map.put(inorder[i], i);
        }

这个代码就讲的很明白key是中序数组的值，value是前序数组的对应下标。
继续讲之后的步骤。递归中先把整个中序数组全放进去，再一部分一部分的处理。具体是怎么部分处理的呢？先获取根节点，再从中序数组中找到它的子树们，再对子树进行判断，其实注解已经讲得很详细了。
最后放出在牛客跑通的代码：

public class Solution {
    //利用原理,先序遍历的第一个节点就是根。在中序遍历中通过根 区分哪些是左子树的，哪些是右子树的
    //左右子树，递归
    HashMap<Integer, Integer> map = new HashMap<>();//标记中序遍历
    int[] preorder;//保留的先序遍历
    public TreeNode reConstructBinaryTree(int [] pre,int [] vin) {
         this.preorder = pre;
        for (int i = 0; i < preorder.length; i++) {
            map.put(vin[i], i);
        }
        return recursive(0,0,vin.length-1);
    }
    public TreeNode recursive(int pre_root_idx, int in_left_idx, int in_right_idx) {
        //相等就是自己
        if (in_left_idx > in_right_idx) {
            return null;
        }
        //root_idx是在先序里面的
        TreeNode root = new TreeNode(preorder[pre_root_idx]);
        // 有了先序的,再根据先序的，在中序中获 当前根的索引
        int idx = map.get(preorder[pre_root_idx]);

        //左子树的根节点就是 左子树的(前序遍历）第一个，就是+1,左边边界就是left，右边边界是中间区分的idx-1
        root.left = recursive(pre_root_idx + 1, in_left_idx, idx - 1);

        //由根节点在中序遍历的idx 区分成2段,idx 就是根

        //右子树的根，就是右子树（前序遍历）的第一个,就是当前根节点 加上左子树的数量
        // pre_root_idx 当前的根  左子树的长度 = 左子树的左边-右边 (idx-1 - in_left_idx +1) 。最后+1就是右子树的根了
        root.right = recursive(pre_root_idx + (idx-1 - in_left_idx +1)  + 1, idx + 1, in_right_idx);
        return root;
    }
}

思路很牛，简洁可读性强，学习了，希望下次自己在遇到这个题可以一下子写出来。