代码随想录Day10--二叉树02-拓展
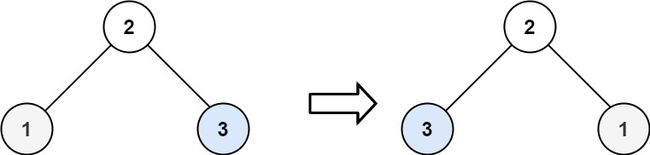
226 反转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
输入:root = [4,2,7,1,3,6,9] 输出:[4,7,2,9,6,3,1]
示例 2:
输入:root = [2,1,3] 输出:[2,3,1]
示例 3:
输入:root = [] 输出:[]
提示:
- 树中节点数目范围在
[0, 100]内 -100 <= Node.val <= 100
解题思路:首先我们使用了迭代法来翻转二叉树。我们使用一个栈来保存需要翻转的节点。首先,我们将根节点压入栈中。然后,我们循环执行以下操作,直到栈为空:
- 弹出栈顶节点
current。 - 交换
current的左右子树。 - 如果
current的左子树不为空,将左子树压入栈中。 - 如果
current的右子树不为空,将右子树压入栈中。
最后,我们返回根节点即可。
方法二: 递归法。在 invertTree 方法中,我们首先检查根节点是否为空。如果为空,则返回 null。否则,我们交换根节点的左右子树,然后递归地翻转左右子树。最后,我们返回根节点。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode invertTree(TreeNode root) {
//迭代法
if(root==null) return null;
Stack stack=new Stack<>();
stack.push(root);
while(!stack.isEmpty()){
TreeNode current=stack.pop();
TreeNode temp=current.left;
current.left=current.right;
current.right=temp;
if(current.left!=null){
stack.push(current.left);
}
if(current.right!=null){
stack.push(current.right);
}
}
return root;
}
}
//方法二:递归法
//递归法
class Solution {
public TreeNode invertTree(TreeNode root) {
if(root==null) return null;
TreeNode temp=root.left;
root.left=root.right;
root.right=temp;
invertTree(root.left);
invertTree(root.right);
return root;
}
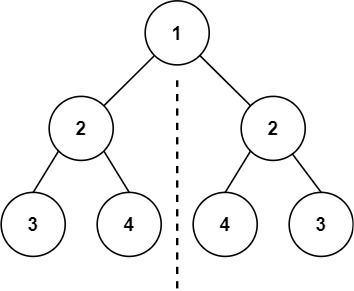
} 101 对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
输入:root = [1,2,2,3,4,4,3] 输出:true
示例 2:
输入:root = [1,2,2,null,3,null,3] 输出:false
解题思路:在这个代码中,isMirror函数就是用来判断两棵二叉树是否是镜像的。如果两个节点都为空,那么它们是镜像的;如果一个节点为空而另一个不为空,那么它们不是镜像的;如果两个节点的值相等,那么它们的左子树和右子树分别与对方的右子树和左子树镜像,那么它们就是镜像的。在isSymmetric函数中,我们只是调用了isMirror函数,参数是根节点和自身,因为一个对称的二叉树的左子树和右子树是镜像的。
class Solution {
public boolean isSymmetric(TreeNode root) {
if(root==null) return false;
return isMirror(root,root);
}
private boolean isMirror(TreeNode t1,TreeNode t2){
if(t1==null && t2==null){
return true;
}else if(t1!=null && t2!=null){
return t1.val==t2.val && isMirror(t1.left,t2.right) && isMirror(t1.right,t2.left);
}
return false;
}
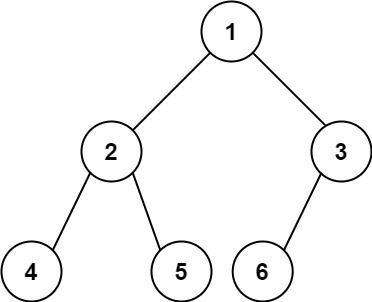
}104 二叉树的最大深度
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
输入:root = [3,9,20,null,null,15,7] 输出:3
示例 2:
输入:root = [1,null,2] 输出:2
解题思路:迭代法:先检查根节点是否为空。如果根节点为空,那么树的最大深度为0。然后,我们创建一个队列并将根节点添加到队列中。然后,我们开始一个循环,该循环将继续,直到队列为空。在每个循环中,我们首先获取当前层级的节点数(即队列的大小),并将其加到最大深度中。然后,我们遍历当前层级的所有节点,将每个节点的左子节点和右子节点添加到队列中(如果它们存在的话)。在遍历完当前层级的所有节点后,我们进入下一层级。这个过程将继续,直到队列为空,这意味着我们已经遍历了整棵树。最后,我们返回最大深度。
递归法:首先检查根节点是否为空。如果根节点为空,那么树的最大深度为0。然后,我们递归地计算左子树和右子树的最大深度。最后,我们返回左子树和右子树最大深度的最大值,并加1(加1是因为要加上根节点本身的深度)。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
//迭代法
class Solution {
public int maxDepth(TreeNode root) {
int maxDepth=0;
if(root==null) return maxDepth;
Queue queue=new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()){
maxDepth++;
int levelSize=queue.size();
for(int i=0;i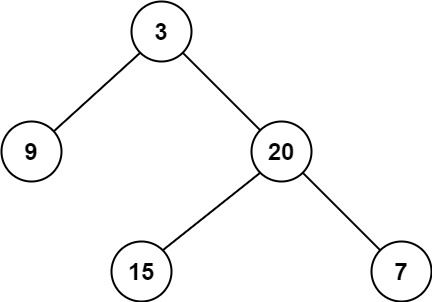
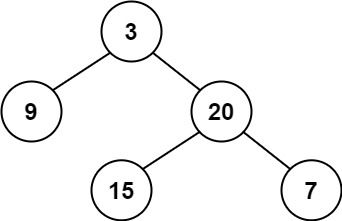
输入:root = [3,9,20,null,null,15,7]
输出:2
示例 2:
输入:root = [2,null,3,null,4,null,5,null,6]
输出:5
解题思路:分别用迭代法和递归法实现
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
//方法一:递归法
//我们首先检查root是否为空,如果为空则返回0。然后,我们检查root是否为叶子节点(即没有左子节点和右子节点),如果是,则返回1,因为最小深度为1。
//如果root不是叶子节点,我们就递归地计算左子树和右子树的最小深度,并将它们存储在leftDepth和rightDepth变量中。然后,我们返回左子树和右子树最小深度的较小值加1(加1是因为要加上根节点本身的深度)。
public int minDepth(TreeNode root) {
if(root==null) return 0;
if(root.left==null && root.right==null)
return 1;
int leftDepth=Integer.MAX_VALUE;
if(root.left!=null){
leftDepth=minDepth(root.left);
}
int rightDepth=Integer.MAX_VALUE;
if(root.right!=null){
rightDepth=minDepth(root.right);
}
return Math.min(leftDepth,rightDepth)+1; //(加1是因为要加上根节点本身的深度)
}
}
//方法二:递归法
//首先检查根节点是否为空。如果根节点为空,那么树的最小深度为0。然后,我们创建一个队列并将根节点添加到队列中。然后,我们开始一个循环,该循环将继续,直到队列为空。在每个循环中,二叉树的深度+1,直到发现某节点为叶子结点,退出循环返回深度值,该值即为最小深度值。
class Solution {
public int minDepth(TreeNode root) {
int depth=0;
if (root == null) {
return 0;
}
Queue queue = new LinkedList<>();
queue.add(root);
int minDepth = Integer.MAX_VALUE;
while (!queue.isEmpty()) {
depth++;
int levelSize = queue.size();
for (int i = 1; i <= levelSize; i++) {
TreeNode node = queue.poll();
if (node.left == null && node.right == null) {
//depth++; 自增写在这,depth最大值为2
/*
System.out.println(node.val);
System.out.println("depth="+depth); 测试用
*/
// 当前节点为叶子节点,更新最小深度
return depth;
} else {
// 将子节点加入队列
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
}
}
return 0;
}
}
222 完全二叉树的节点个数
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
示例 1:
输入:root = [1,2,3,4,5,6]
输出:6
示例 2:
输入:root = []
输出:0
示例 3:
输入:root = [1]
输出:1
解题思路:用递归法和迭代法实现
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
/*
完全二叉树的定义是一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同。
从满二叉树和完全二叉树的定义可以看出,满二叉树是完全二叉树的特殊形态,即如果一棵二叉树是满二叉树,则它必定是完全二叉树。
*/
//方法一:递归法
/*
countNodes函数是公开的接口,它首先检查根节点是否为空。如果为空,则返回0。否则,它调用辅助函数countNodesHelper来计算节点个数。
countNodesHelper函数是一个递归函数,它接受一个节点作为参数。否则,递归地计算左子树和右子树的节点个数,并将它们相加,最后再加上当前节点(根节点算一个节点),即得到总的节点个数。
这个算法的时间复杂度是O(log^2 N),其中N是节点的数量
*/
class Solution {
public int countNodes(TreeNode root) {
if (root == null) {
return 0;
}
return countNodesHelper(root);
}
private int countNodesHelper(TreeNode node) {
if (node == null) {
return 0;
}
return countNodesHelper(node.left) + countNodesHelper(node.right) + 1;
}
}
//方法二:层序遍历——使用一个队列来进行广度优先搜索(BFS)
class Solution {
public int countNodes(TreeNode root) {
if (root == null) {
return 0;
}
Queue queue = new LinkedList<>();
queue.add(root);
int levelCount = 1; // 第一层有一个节点
int totalCount = 0;
while (!queue.isEmpty()) {
int levelSize = queue.size();
totalCount += levelSize;
levelCount++; //可用来计算完全二叉树的层数
for (int i = 0; i < levelSize; i++) {
TreeNode node = queue.poll();
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
}
return totalCount;
}
}
110 平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
示例 1:
输入:root = [3,9,20,null,null,15,7]
输出:true
示例 2:
输入:root = [1,2,2,3,3,null,null,4,4]
输出:false
示例 3:
输入:root = []
输出:true
解题思路:方法一,用递归法实现,在这个方案中:isBalanced 方法检查树的根节点是否是平衡的。如果根节点是 null,则树是平衡的。否则,我们检查树的左子树和右子树的高度差是否不超过 1,并且左右子树也都是平衡的。height 方法计算了树的高度。如果一个节点是 null,那么它的高度是 0,否则它的高度是左右子树中较高的一个加 1。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isBalanced(TreeNode root) {
if(root==null)
return true;
//Math.abs(x) 返回一个数x的绝对值
return Math.abs(height(root.left)-height(root.right))<=1 && isBalanced(root.left) && isBalanced(root.right);
}
private int height(TreeNode node){
if(node==null)
return 0;
return Math.max(height(node.right),height(node.left))+1;
}
}
方法二:迭代法,使用栈来存储每个节点的父节点,这样我们就可以轻松地在回溯过程中获取每个节点的左右子节点。
使用一个辅助栈来保存待处理的节点,并使用一个哈希表 `heights` 来保存每个节点的高度。我们使用一个循环来遍历每个节点,当节点的左右子树的高度差超过1时,返回 `false`。对于已经遍历完左右子树的节点,我们更新其高度,并将其从栈中弹出。对于未遍历完左右子树的节点,我们将其左右子树入栈。如果循环结束后没有发现高度差超过1的节点,则返回 `true`,表明该二叉树是高度平衡的。
public class Solution {
public boolean isBalanced(TreeNode root) {
if (root == null) {
return true;
}
// 使用一个辅助栈来保存待处理的节点
Stack stack = new Stack<>();
// 使用一个哈希表来保存每个节点的高度
Map heights = new HashMap<>();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.peek();
// 如果左子树和右子树的高度差超过1,返回false
if ((node.left != null && heights.getOrDefault(node.left, 0) - heights.getOrDefault(node.right, 0) > 1) ||
(node.right != null && heights.getOrDefault(node.right, 0) - heights.getOrDefault(node.left, 0) > 1)) {
return false;
}
// 如果当前节点的左右子树已经遍历完,则更新当前节点的高度
if ((node.left == null || heights.containsKey(node.left)) && (node.right == null || heights.containsKey(node.right))) {
int leftHeight = heights.getOrDefault(node.left, 0);
int rightHeight = heights.getOrDefault(node.right, 0);
heights.put(node, Math.max(leftHeight, rightHeight) + 1);
stack.pop();
} else {
// 否则,将左右子树入栈
if (node.left != null && !heights.containsKey(node.left)) {
stack.push(node.left);
}
if (node.right != null && !heights.containsKey(node.right)) {
stack.push(node.right);
}
}
}
return true;
}
}
257 二叉树的所有路径
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
示例 1:
输入:root = [1,2,3,null,5]
输出:["1->2->5","1->3"]
示例 2:
输入:root = [1]
输出:["1"]
解题思路:递归
`TreeNode`是表示二叉树节点的自定义类。`binaryTreePaths`方法接受二叉树的根节点作为参数,并返回一个包含所有从根节点到叶子节点的路径的字符串列表。
在`dfs`方法中,我们使用深度优先搜索来遍历二叉树。当遍历到叶子节点时,我们将完整路径添加到结果列表中。对于每个非叶子节点,我们将当前节点的值添加到路径中,并递归地搜索左子树和右子树。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List binaryTreePaths(TreeNode root) {
List paths = new ArrayList<>();
if (root != null) {
dfs(root, "", paths);
}
return paths;
}
private void dfs(TreeNode node, String path, List paths) {
if (node.left == null && node.right == null) {
// 叶子节点,将完整路径添加到结果列表中
paths.add(path + node.val);
}
if (node.left != null) {
// 深度优先搜索左子树
dfs(node.left, path + node.val + "->", paths);
}
if (node.right != null) {
// 深度优先搜索右子树
dfs(node.right, path + node.val + "->", paths);
}
}
}
404 左叶子之和
给定二叉树的根节点 root ,返回所有左叶子之和。
示例 1:
输入: root = [3,9,20,null,null,15,7]
输出: 24
解释: 在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24
示例 2:
输入: root = [1]
输出: 0
解题思路:通过递归遍历来实现,
`TreeNode`是表示二叉树节点的自定义类。`sumOfLeftLeaves`方法接受二叉树的根节点作为参数,并返回所有左叶子节点的和。
在递归的过程中,我们首先判断当前节点的左子节点是否为叶子节点(即左子节点的左右子节点均为空)。如果是左叶子节点,则将左叶子节点的值加到左叶子和`leftSum`中。
然后,我们递归地遍历当前节点的左子树和右子树,并将结果加到左叶子和`leftSum`中。
**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int sumOfLeftLeaves(TreeNode root) {
if (root == null) {
return 0;
}
int leftSum = 0;
// 判断左子节点是否为叶子节点
if (root.left != null && root.left.left == null && root.left.right == null) {
leftSum += root.left.val; // 将左叶子节点的值加到左叶子和中
}
// 递归遍历左子树和右子树,并将结果加到左叶子和中
leftSum += sumOfLeftLeaves(root.left);
leftSum += sumOfLeftLeaves(root.right);
return leftSum;
}
}