1021.从前有座山

Description

从前有座山，山的俯视图是一个n×n的矩形，(1,1)位置海拔最低为1，然后海拔沿环形依次升高。

给定n的值，输出这座山的海拔高度图。

Input Format

输入仅有一行，为一个正整数n。

Output Format

输出为这座山的海拔高度图。

Sample Input

4

Sample Output

     1     2     3     4

    12    13    14     5

    11    16    15     6

    10     9     8     7

 

---

 

题源上交acm，地址http://acm.sjtu.edu.cn/OnlineJudge/problem/1021

google了一下，网上现有的做法似乎都没有我的好，所以把我的做法贴出来^_^

 

基本的思路是开辟一个n * n的矩阵，填上表示高度的数字，再输出这个矩阵。

问题在于如何填上正确的数字。

 

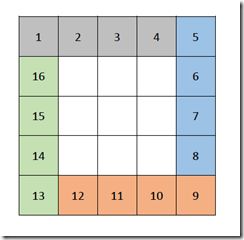
以 n = 5 为例子，观察最外圈的数字，将其分为4个部分，如图

显然，每个部分都可以用一个循环来填充数字。不失一般的，填充一整圈的伪代码为：

for i = 1 .. N-1

    map[1][i] = i

    map[i][N] = N - 1 + i

    map[N][N - i] = 2 * (N - 1) + i

    map[N - i][1]= 3 * (N - 1) + i

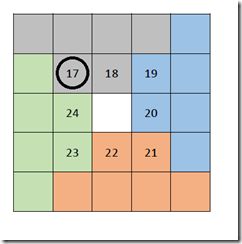
对于非最外圈而言，记录下起始填充位置的偏移量（包括x轴偏移，y轴偏移，填充数字偏移）即可。

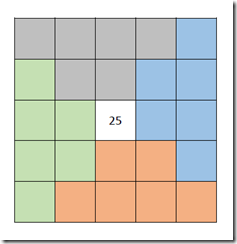
最后，对于奇数边长矩阵，需要在矩阵的中心点填上高度的最大值，也就是边长的平方。

---

#include <iostream>

#include <iomanip>

#include <string.h>



using namespace std;



int main(){



	int i, j;

	int n;

	int *map;



	cin >> n;

	map = new int[n * n];

	memset(map, 0, sizeof(map));



	int h_offset = 1;

	int x_offset = 0;

	int y_offset = 0;



	for (int len = n - 1; len > 0; len-= 2){	//a loop fills a circle, from outer to inner



		for (i = 0; i < len; ++i){

			

			map[x_offset * n + (y_offset + i)] = h_offset + i;

			map[(x_offset + i) * n +  (n - 1 - y_offset)] = h_offset + len + i;

			map[(n - 1 - x_offset) * n + (n - 1 - y_offset - i)] = h_offset + 2 * len + i;

			map[(n - 1 - x_offset - i) * n + (y_offset)] = h_offset + 3 * len + i;



		}



		h_offset += 4 * len;

		x_offset ++;

		y_offset ++;



	}



	if(n % 2 == 1)

		map[n * n / 2] = n * n;



	for (i = 0; i < n; ++i){

		for (j = 0; j < n; ++j){

			cout << setw(6) << map[i * n + j];

		}

		cout << endl;

	}



	delete []map;

	return 0;

}