数据结构C#版笔记--单链表(LinkList)
上一篇学习了"顺序表(SeqList)",这一篇来看下“单链表(LinkList)”。在上一篇的最后,我们指出了:顺序表要求开辟一组连续的内存空间,而且插入/删除元素时,为了保证元素的顺序性,必须对后面的元素进行移动。如果你的应用中需要频繁对元素进行插入/删除,那么开销会很大。
而链表结构正好相反,先来看下结构:
每个元素至少具有二个属性:data和next。data用来存放数据,而next用来指出它后面的元素是谁(有点“指针”的意思)。
链表中的元素,通常也称为节点Node,下面是泛型版本的Node.cs
namespace 线性表
{
public class Node<T>
{
private T data;
private Node<T> next;
public Node(T val, Node<T> p)
{
data = val;
next = p;
}
public Node(Node<T> p)
{
next = p;
}
public Node(T val)
{
data = val;
next = null;
}
public Node()
{
data = default(T);
next = null;
}
public T Data
{
get { return data; }
set { data = value; }
}
public Node<T> Next
{
get { return next; }
set { next = value; }
}
}
}
链表在存储上并不要求所有元素按顺序存储,因为用节点的next就能找到下一个节点,这好象一根“用珠子串成的链子”,要找到其中的某一颗珠子,只要从第一
颗节点(通常称为Head节点)开始,不断根据next指向找到下一个,直到找到需要的节点为止。
链表中需要有一个Head节点做为开始,这跟顺序表有所不同,下面是单链表的实现:
using System;
using System.Text;
namespace 线性表
{
public class LinkList<T> : IListDS<T>
{
private Node<T> head;
public Node<T> Head
{
get { return head; }
set { head = value; }
}
public LinkList()
{
head = null;
}
/// <summary>
/// 类索引器
/// </summary>
/// <param name="index"></param>
/// <returns></returns>
public T this[int index]
{
get
{
return this.GetItemAt(index);
}
}
/// <summary>
/// 返回单链表的长度
/// </summary>
/// <returns></returns>
public int Count()
{
Node<T> p = head;
int len = 0;
while (p != null)
{
len++;
p = p.Next;
}
return len;
}
/// <summary>
/// 清空
/// </summary>
public void Clear()
{
head = null;
}
/// <summary>
/// 是否为空
/// </summary>
/// <returns></returns>
public bool IsEmpty()
{
return head == null;
}
/// <summary>
/// 在最后附加元素
/// </summary>
/// <param name="item"></param>
public void Append(T item)
{
Node<T> d = new Node<T>(item);
Node<T> n = new Node<T>();
if (head == null)
{
head = d;
return;
}
n = head;
while (n.Next != null)
{
n = n.Next;
}
n.Next = d;
}
//前插
public void InsertBefore(T item, int i)
{
if (IsEmpty() || i < 0)
{
Console.WriteLine("List is empty or Position is error!");
return;
}
//在最开头插入
if (i == 0)
{
Node<T> q = new Node<T>(item);
q.Next = Head;//把"头"改成第二个元素
head = q;//把自己设置为"头"
return;
}
Node<T> n = head;
Node<T> d = new Node<T>();
int j = 0;
//找到位置i的前一个元素d
while (n.Next != null && j < i)
{
d = n;
n = n.Next;
j++;
}
if (n.Next == null) //说明是在最后节点插入(即追加)
{
Node<T> q = new Node<T>(item);
n.Next = q;
q.Next = null;
}
else
{
if (j == i)
{
Node<T> q = new Node<T>(item);
d.Next = q;
q.Next = n;
}
}
}
/// <summary>
/// 在位置i后插入元素item
/// </summary>
/// <param name="item"></param>
/// <param name="i"></param>
public void InsertAfter(T item, int i)
{
if (IsEmpty() || i < 0)
{
Console.WriteLine("List is empty or Position is error!");
return;
}
if (i == 0)
{
Node<T> q = new Node<T>(item);
q.Next = head.Next;
head.Next = q;
return;
}
Node<T> p = head;
int j = 0;
while (p != null && j < i)
{
p = p.Next;
j++;
}
if (j == i)
{
Node<T> q = new Node<T>(item);
q.Next = p.Next;
p.Next = q;
}
else
{
Console.WriteLine("Position is error!");
}
}
/// <summary>
/// 删除位置i的元素
/// </summary>
/// <param name="i"></param>
/// <returns></returns>
public T RemoveAt(int i)
{
if (IsEmpty() || i < 0)
{
Console.WriteLine("Link is empty or Position is error!");
return default(T);
}
Node<T> q = new Node<T>();
if (i == 0)
{
q = head;
head = head.Next;
return q.Data;
}
Node<T> p = head;
int j = 0;
while (p.Next != null && j < i)
{
j++;
q = p;
p = p.Next;
}
if (j == i)
{
q.Next = p.Next;
return p.Data;
}
else
{
Console.WriteLine("The node is not exist!");
return default(T);
}
}
/// <summary>
/// 获取指定位置的元素
/// </summary>
/// <param name="i"></param>
/// <returns></returns>
public T GetItemAt(int i)
{
if (IsEmpty())
{
Console.WriteLine("List is empty!");
return default(T);
}
Node<T> p = new Node<T>();
p = head;
if (i == 0)
{
return p.Data;
}
int j = 0;
while (p.Next != null && j < i)
{
j++;
p = p.Next;
}
if (j == i)
{
return p.Data;
}
else
{
Console.WriteLine("The node is not exist!");
return default(T);
}
}
//按元素值查找索引
public int IndexOf(T value)
{
if (IsEmpty())
{
Console.WriteLine("List is Empty!");
return -1;
}
Node<T> p = new Node<T>();
p = head;
int i = 0;
while (!p.Data.Equals(value) && p.Next != null)
{
p = p.Next;
i++;
}
return i;
}
/// <summary>
/// 元素反转
/// </summary>
public void Reverse()
{
LinkList<T> result = new LinkList<T>();
Node<T> t = this.head;
result.Head = new Node<T>(t.Data);
t = t.Next;
//(把当前链接的元素从head开始遍历,逐个插入到另一个空链表中,这样得到的新链表正好元素顺序跟原链表是相反的)
while (t!=null)
{
result.InsertBefore(t.Data, 0);
t = t.Next;
}
this.head = result.head;//将原链表直接挂到"反转后的链表"上
result = null;//显式清空原链表的引用,以便让GC能直接回收
}
public override string ToString()
{
StringBuilder sb = new StringBuilder();
Node<T> n = this.head;
sb.Append(n.Data.ToString() + ",");
while (n.Next != null)
{
sb.Append(n.Next.Data.ToString() + ",");
n = n.Next;
}
return sb.ToString().TrimEnd(',');
}
}
}
下面是单链表插入和删除的算法图解:
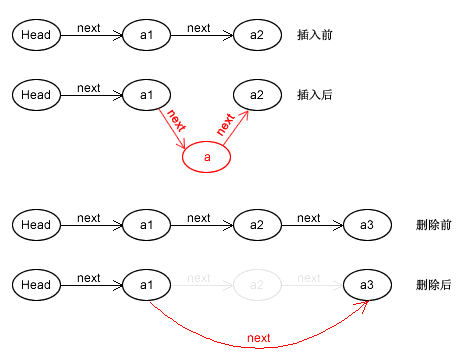
可以看到:链表在元素插入/删除时,无需对后面的元素进行移动,只需要修改自身以及相邻节点的next指向即可,所以插入/删除元素的开销要比顺序表小得多。但是也应该注意到,其它操作比如:查找元素,反转倒置链表等,有可能需要遍历整个链表中的所有元素。
测试代码片断:
Console.WriteLine("-------------------------------------");
Console.WriteLine("单链表测试开始...");
LinkList<string> link = new LinkList<string>();
link.Head = new Node<string>("x");
link.InsertBefore("w", 0);
link.InsertBefore("v", 0);
link.Append("y");
link.InsertBefore("z", link.Count());
Console.WriteLine(link.Count());//5
Console.WriteLine(link.ToString());//v,w,x,y,z
Console.WriteLine(link[1]);//w
Console.WriteLine(link[0]);//v
Console.WriteLine(link[4]);//z
Console.WriteLine(link.IndexOf("z"));//4
Console.WriteLine(link.RemoveAt(2));//x
Console.WriteLine(link.ToString());//v,w,y,z
link.InsertBefore("x", 2);
Console.WriteLine(link.ToString());//v,w,x,y,z
Console.WriteLine(link.GetItemAt(2));//x
link.Reverse();
Console.WriteLine(link.ToString());//z,y,x,w,v
link.InsertAfter("1", 0);
link.InsertAfter("2", 1);
link.InsertAfter("6", 5);
link.InsertAfter("8", 7);
link.InsertAfter("A", 10);//Position is error!
Console.WriteLine(link.ToString()); //z,1,2,y,x,w,6,v,8
至于具体在实际应用中应该选用顺序表 or 链表,主要是看:对于元素插入/删除的频繁程度以及对于内存分配的苛刻程度。 如果不要求一开始就分配一组连续的内存区域,可以根据元素的增加而自动加大内存的使用量,或者插入/删除的次数很多,那么建议使用链表,反之用顺序表。
最后指出:可以给节点再添加一个prev元素,用于指出前一个节点是谁,即同时有next和prev二个指向,这种改进后的链表称为“双向链表”,它有助于某些情况下减少遍历循环的次数,本文中的这种仅有一个next指向的链表,称为“单链表”。