A Round Peg in a Ground Hole(判断是否是凸包，点是否在凸包内，圆与多边形的关系)

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 4628		Accepted: 1434

Description

The DIY Furniture company specializes in assemble-it-yourself furniture kits. Typically, the pieces of wood are attached to one another using a wooden peg that fits into pre-cut holes in each piece to be attached. The pegs have a circular cross-section and so are intended to fit inside a round hole. 
A recent factory run of computer desks were flawed when an automatic grinding machine was mis-programmed. The result is an irregularly shaped hole in one piece that, instead of the expected circular shape, is actually an irregular polygon. You need to figure out whether the desks need to be scrapped or if they can be salvaged by filling a part of the hole with a mixture of wood shavings and glue. 
There are two concerns. First, if the hole contains any protrusions (i.e., if there exist any two interior points in the hole that, if connected by a line segment, that segment would cross one or more edges of the hole), then the filled-in-hole would not be structurally sound enough to support the peg under normal stress as the furniture is used. Second, assuming the hole is appropriately shaped, it must be big enough to allow insertion of the peg. Since the hole in this piece of wood must match up with a corresponding hole in other pieces, the precise location where the peg must fit is known. 
Write a program to accept descriptions of pegs and polygonal holes and determine if the hole is ill-formed and, if not, whether the peg will fit at the desired location. Each hole is described as a polygon with vertices (x1, y1), (x2, y2), . . . , (xn, yn). The edges of the polygon are (xi, yi) to (x _i+1, y _i+1) for i = 1 . . . n − 1 and (xn, yn) to (x1, y1).

Input

Input consists of a series of piece descriptions. Each piece description consists of the following data: 
Line 1 < nVertices > < pegRadius > < pegX > < pegY > 
number of vertices in polygon, n (integer) 
radius of peg (real) 
X and Y position of peg (real) 
n Lines < vertexX > < vertexY > 
On a line for each vertex, listed in order, the X and Y position of vertex The end of input is indicated by a number of polygon vertices less than 3.

Output

For each piece description, print a single line containing the string: 
HOLE IS ILL-FORMED if the hole contains protrusions 
PEG WILL FIT if the hole contains no protrusions and the peg fits in the hole at the indicated position 
PEG WILL NOT FIT if the hole contains no protrusions but the peg will not fit in the hole at the indicated position

Sample Input

5 1.5 1.5 2.0

1.0 1.0

2.0 2.0

1.75 2.0

1.0 3.0

0.0 2.0

5 1.5 1.5 2.0

1.0 1.0

2.0 2.0

1.75 2.5

1.0 3.0

0.0 2.0

1

Sample OutputHOLE IS ILL-FORMED

PEG WILL NOT FIT

题意：给n个点的坐标，以及一个圆的圆心和半径。
　　　判断这n个点能否形成凸包，若不能输出“HOLE IS ILL-FORMED”，否则，再判断圆心以及整个圆是否在凸多边形内；

思路： 分三步；
先形成一个封闭的多边形，
1.判断是否是凸包，循环取相邻的两条边，作叉乘，若结果为负说明不是凸包；

2.判断圆心是否在凸多边形内，

用环顾法：

   设圆心为P，逐条枚举n边形的边AB，利用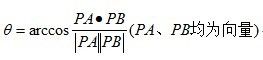 

 

   计算PA和PB的夹角，最后求和得到的就是环顾角。

（1）       圆心在多边形内部时，环顾角=±360

（2）       圆心在多边形外部时，环顾角=0

（3）       圆心在多边形边上时（不包括顶点），环顾角=±180

（4）       圆心在多边形顶点时，环顾角为(0,360)之间的任意角，其实就是圆心所在的顶点的两条邻接边的夹角。

3.判断圆与多边形的关系；

　当圆与多边形每条边的距离都小于半径时，说明圆在多边形内部。

  1 #include<stdio.h>

  2 #include<string.h>

  3 #include<math.h>

  4 const double eps = 1e-8;

  5 const double PI = 3.1415926535898;

  6 int cmp(double x)

  7 {

  8     if(fabs(x) < eps)

  9         return 0;

 10     if(x > 0)

 11         return 1;

 12     return -1;

 13 }

 14 int n;//多边形点的个数

 15 double r;//钉子半径

 16 

 17 struct Point

 18 {

 19     double x,y;

 20     Point (){}

 21     Point(double a,double b):x(a),y(b) {}

 22 }point[110],p;//p为钉子坐标

 23 //叉乘

 24 double det(double x1,double y1,double x2,double y2)

 25 {

 26     return x1*y2-x2*y1;

 27 }

 28 //分别以a、b和 c、d为端点的两条线段的叉乘

 29 double edge_det(Point a,Point b,Point c,Point d)

 30 {

 31     return det(b.x-a.x,b.y-a.y,d.x-c.x,d.y-c.y);

 32 }

 33 //点乘

 34 double dot(double x1,double y1,double x2,double y2)

 35 {

 36     return x1*x2 + y1*y2;

 37 }

 38 //分别以a、p和 b、p为端点的两条线段的点乘

 39 double edge_dot(const Point &p, const Point &a, const Point &b)

 40 {

 41     return dot(a.x-p.x,a.y-p.y,b.x-p.x,b.y-p.y);

 42 }

 43 //两点间的距离

 44 double dis(const Point &a, const Point &b)

 45 {

 46     return sqrt((a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y));

 47 }

 48 //向量PA和PB 间的夹角

 49 double cal_angle(const Point &a, const Point &b, const Point &p)

 50 {

 51     double res = edge_dot(p,a,b);

 52     double L1 = dis(a,p);

 53     double L2 = dis(b,p);

 54     return acos(res/(L1*L2));

 55 }

 56 

 57 bool is_convex_hull()//判断是否为凸包，任意两相临边作叉乘，若结果为负说明不是凸包；

 58 {

 59     double base = 0;

 60     for(int i = 0; i < n; i++)

 61     {

 62         double tmp = cmp(edge_det(point[i],point[i+1],point[i+1],point[i+2]));

 63         if(!base)

 64             base = tmp;

 65         if(base * tmp < 0)

 66            return false;

 67     }

 68     return true;

 69 }

 70 bool in_convex_hull()//判断圆心是否在凸包内

 71 {

 72     double angle = 0;

 73     for(int i = 1; i <= n; i++)

 74     {

 75         if(cmp(edge_det(p,point[i],p,point[i+1])) >= 0)

 76             angle += cal_angle(point[i],point[i+1],p);

 77         else angle -= cal_angle(point[i],point[i+1],p);

 78     }

 79     if(cmp(angle) == 0)//在多边形外部

 80         return false;

 81     if(cmp(angle+PI) == 0 || cmp(angle-PI) == 0)//在多边形边上，不包括顶点。

 82     {

 83         if(cmp(r) == 0)

 84             return true;

 85     }

 86     if(cmp(angle+2*PI) == 0 || cmp(angle-2*PI) == 0)//在多边形内部；

 87         return true;

 88     else//在多边形顶点上；

 89     {

 90         if(cmp(r) == 0)

 91             return true;

 92     }

 93     return false;

 94 }

 95 bool is_fit()//判断以r为半径的圆是否在凸包内

 96 {

 97     for(int i = 0; i < n; i++)

 98     {

 99         double res = fabs(edge_det(point[i],p,point[i+1],p)/dis(point[i],point[i+1]));

100         if(cmp(res-r) < 0)

101             return false;

102     }

103     return true;

104 }

105 int main()

106 {

107     while(~scanf("%d",&n) && n >= 3)

108     {

109         scanf("%lf %lf %lf",&r,&p.x,&p.y);

110 

111         for(int i = 0; i < n; i++)

112             scanf("%lf %lf",&point[i].x,&point[i].y);

113 

114         point[n] = point[0];

115         point[n+1] = point[1];

116 

117         if (!is_convex_hull())//不是一个凸包；

118         {

119             printf("HOLE IS ILL-FORMED\n");

120             continue;

121         }

122         bool f1 = in_convex_hull();

123         bool f2 = is_fit();

124         if(f1 && f2)

125             printf("PEG WILL FIT\n");

126         else printf("PEG WILL NOT FIT\n");

127 

128     }

129     return 0;

130 }

View Code