算法导论13章之红黑树
没有三两三,哪敢上梁山,在读此篇之前,请保证基本的BST知识和红黑树的知识!
为了保证对于规模为n输入的一些基本操作的复杂度在O(lgn)内,一般是建立平衡树,一般的有AVL树,2-3树,2-3-4树,跳跃表,当然一般效率很好的是红黑树,SGL STL 实现关联容器就是使用的红黑树,也是基于效率的考虑。那到底什么事红黑树呢?
首先介绍红黑树的结点,有color、key、parent、left、right五个域,其中color表示树结点的颜色(有红、黑两种),其余四个域不言自明。
红黑树是满足一下5条红黑性质的BST树:
① 所有的结点或者是红色的,或者是黑色的;
② 根节点是黑色的;
③ 叶子结点(又称外部结点,用NIL表示)是黑色的;
④ 如果一个结点是红色结点,其左右子节点都是黑色结点;
⑤ 对于红黑树的任意一个结点,其到它的所有子节点的简单路径上有相同的黑色结点(即有相同的黑高)。
这样一棵红黑树保证没有一条路径的长度是任何其他路径的长度的两倍,因此基本上时平衡的。
因为对于规模为n的输入来说,红黑树的高度h<=2log(n+1), 下面给出一个简单的证明:
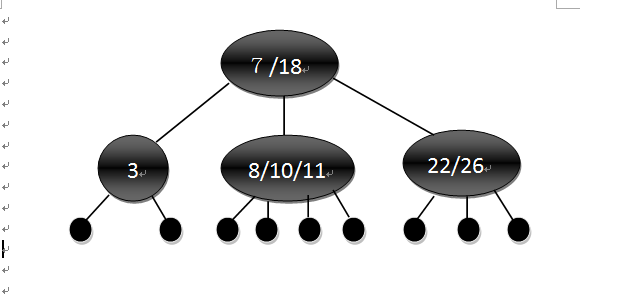
这也是本文的第一个要点,对于如下的一棵红黑树:
将红色结点合并到黑色结点得到如下所示的2-3-4平衡树:
对于规模为n的输入,有n+1个叶子结点,设2-3-4树的高度为h1,则2h1<=n+1<=4h1,则h1<=lg(n+1);设原来的红黑树的高度为h,有红黑树的性质克制:红黑树中的红色结点最多为一半,即h<=2*(h1)<=2lg(n+1)。证毕。
本文的第二个要点是说明如何对插入操作进行修补,使之满足红黑性质:
在开始之前,作为预备知识,有:
A 互换父节点和其左子结点的颜色,然后以父节点进行右旋操作,整棵红黑树的红黑性质不会被破坏,
B 互换父节点和其右子节点的颜色,然后以父节点进行左旋操作,整棵红黑树的红黑性质不会被破坏。
C 每次插入结点的颜色为红色,这样可以保证性质5不会被破坏,而性质5一旦破坏时最男恢复的,只可能破坏性质2和性质4,而性质2和性质4的恢复相对简单。
RB_INSERT_FIXUP的伪码见书上315页,此处不再列出;对性质2的恢复只需设置T.root.color=BLACK即可恢复;对性质4的恢复只要待调整x结点的父节点的颜色变为黑色即恢复了红黑性质。那到底如何恢复性质4呢?
每次循环都将待调整结点向上调整直至父结点的颜色为黑色,或者到了根结点则退出循环,再调整性质2即可。
根据x.p.p.left==x.p是否为真分为两大类,并且这两大类是对称的。下面对一为真的情况给予说明:
此时又分为3种情况:
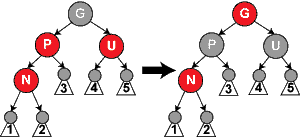
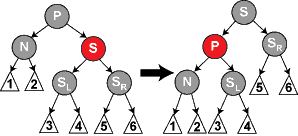
步骤(1)当前结点的叔结点都为红色(父结点显然也为红色,否则已经满足红黑性质了),此时只要将父结点和叔结点的颜色都变为黑色,并将祖父结点由黑色变为红色,再将x结点“上溯”到其祖父结点(即x=x.p.p),如图所示( 变换之前x指向N,变换之后x指向G):
经过这样的变换,没有破坏性质4,并且将x上移了两层哦!
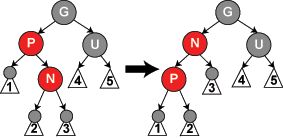
步骤(2)当前结点 x的叔结点的为黑色结点,并且x为其父结点的右子结点,此时令x结点(开始指向N)指向其父结点(x=x.p,调整之后指向P)并以x结点做左旋转操作,转换为情况(3),如下图所示:
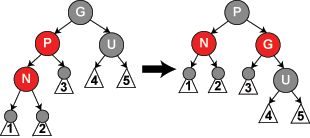
步骤(3)当前结点x的叔结点为黑色结点,并且x为其父结点的左子结点,此时互换x的父结点(图中P)和x的祖父结点(图中G)的颜色,并以祖父结点做右旋转操作,此时已满足所有的红黑性质(由预备知识点A)),退出循环。
对于初学者来说,可能不太明白为什么是这3步操作,还有这3步操作之前的关系。下面我一一道来:
其实最基本的思想是,我们的操作尽可能的不去破坏性质5,改为破坏性质4(也可能破坏其他性质,但都很好恢复),而对于违背性质4的恢复手段来说,就是当前结点x,x的父节点,x的祖父结点,3个结点在一条线上,而不是“Z”型的,此时做预备知识点A或者预备知识点B的操作即可最终恢复性质4,所以会将步骤(2)转换为步骤(3)。对于考虑叔结点的原因除了步骤(1)的很直观的操作之外,就是如果叔结点为红色的话,不能进行步骤(3)的操作,因为操作之后G、U都为红色,从而破坏了性质4。
步骤(1)的复杂度为O(lgh),步骤(2)、(3)的每一步的旋转次数之多为1,所以总的旋转次数不超过2次,故RB_INSERT_FIXUP的复杂度为O(lgn)。
本文的第三个要点讲解对于删除操作之后进行修补:
RB_DELETE_FIXUP操作的伪码见185页,此处不再列出,根据x==x.p.left是否为真分为两大类,同样这两大类是对称的,下面以为真的情况进行说明:
为了不破坏性质5,进而选择破坏性质1、性质2、性质4,所以选择将删除结点的黑色结点“下推”给待调整结点x,以此保持性质5不变;调整的主要任务就是去掉结点x的“下推的黑色”,这主要有两种方法,
方法1、如果x的兄弟结点为黑色(且该结点的两个皆为黑色结点),则将兄弟结点的颜色变为红色,这样就去掉了“下推的黑色",并且x结点指向其父结点(x=x.p),以保持性质性质5,直到x为根结点或者x的颜色为红色,此时只要简单调整即可。
方法2、如果其兄弟结点为黑色结点,且兄弟结点的右子节点为红色,此时,将x的父结点边为黑色,并且以父结点做左旋操作,使得经过x的结点的路径多了一个黑色结点,正好去掉x”下推的黑色“,就已经满足性质2和性质4,退出循环即可。
所以按照此思路共有4中情况:
步骤(1)x(图中N)的兄弟结点(图中S)为红色结点,互换父结点(图中P)和兄弟结点的颜色,并以父结点做左旋转操作(由预备知识点B),不会破坏红黑性质,转换为步骤(2)、(3)、(4)的情况,如下图所示:
步骤(2)对应于方法1,x结点(图中N),兄弟结点为图中S,操作完成之后x为图中P,如下图所示:
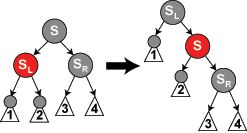
步骤(3)x(图中未画出)的兄弟结点(图中S)为黑色结点,其左子结点(图中SL)为红色,右子结点(图中国SR)为黑色,互换SL和S的颜色并以S做右旋转操作,将情况转为为步骤(4),做转换的原因是,使得转换后的S结点为红色,在步骤(4)调整为黑色,用来弥补将兄弟结点变为父结点颜色带来的黑色结点减少,使得S所在简单路径上的黑色结点数不变,保持性质5.
步骤(4)到了终极解决方法了,对应于方法2,操作如下图所示:
显然步骤(2)的复杂度为O(lgh),步骤(1)、(3)、(4)的每一步的调整最多一次,所以总共的调整次数不超过3次,RB_DELETE_FIXUP的复杂度为O(lgn)。我想旋转次数少,是能体现RB树相较于AVL树的优势的地方吧。
最后,贴出C++实现的代码:
#include <iostream> #include <stack> using namespace std; enum Color{RED=0,BLACK=1}; template<class T> struct RedBlackTreeNode { RedBlackTreeNode():color(BLACK),key(T()),parent(NULL),left(NULL),right(NULL){} int color; T key; RedBlackTreeNode<T>* parent; RedBlackTreeNode<T>* left; RedBlackTreeNode<T>* right; }; template<class T> class RedBlackTree { public: RedBlackTree(){root=NULL;}; ~RedBlackTree(){}; int get_maximum(T& ret) const; int get_minimum(T& ret) const; int get_successor(const T& k,T& ret) const; int get_predecessor(const T& k,T& ret) const; bool search_element(const T& k) const; int insert_key(const T& key); int delete_key(const T& key); RedBlackTreeNode<T>* get_root() const; void inorder_tree_walk() const; private: RedBlackTreeNode<T>* root; static RedBlackTreeNode<T>* NIL; RedBlackTreeNode<T>* get_maximum(RedBlackTreeNode<T>* pnode) const; RedBlackTreeNode<T>* get_minimum(RedBlackTreeNode<T>* pnode) const; RedBlackTreeNode<T>* get_successor(RedBlackTreeNode<T>* pnode) const; RedBlackTreeNode<T>* get_predecessor(RedBlackTreeNode<T>* pnode) const; RedBlackTreeNode<T>* get_parent(RedBlackTreeNode<T>* pnode) const; RedBlackTreeNode<T>* get_left(RedBlackTreeNode<T>* pnode) const; RedBlackTreeNode<T>* get_right(RedBlackTreeNode<T>* pnode) const; int get_color(RedBlackTreeNode<T>* pnode) const; void set_color(RedBlackTreeNode<T>* pnode,const int& color); void left_rotate(RedBlackTreeNode<T>* pnode); void right_rotate(RedBlackTreeNode<T>* pnode); void rb_insert_fixup(RedBlackTreeNode<T>* pnode); void rb_delete_fixup(RedBlackTreeNode<T>* pnode); void rb_transplant(RedBlackTreeNode<T>* oldnode,RedBlackTreeNode<T>* newnode); RedBlackTreeNode<T>* search_tree_node(const T& k) const; int get_key(RedBlackTreeNode<T>* pnode) const; void make_empty(RedBlackTreeNode<T>* root); }; template<class T> RedBlackTreeNode<T>* RedBlackTree<T>::get_root() const { return root; } template<class T> RedBlackTreeNode<T>* RedBlackTree<T>::NIL=new RedBlackTreeNode<T>(); template<class T> RedBlackTreeNode<T>* RedBlackTree<T>::get_maximum(RedBlackTreeNode<T>* pnode) const { while(pnode->right!=NIL) pnode=pnode->right; return pnode; } template<class T> RedBlackTreeNode<T>* RedBlackTree<T>::get_minimum(RedBlackTreeNode<T>* pnode) const { while(pnode->left!=NIL) pnode=pnode->left; return pnode; } template<class T> RedBlackTreeNode<T>* RedBlackTree<T>::get_parent(RedBlackTreeNode<T>* pnode) const { return pnode->parent; } template<class T> RedBlackTreeNode<T>* RedBlackTree<T>::get_left(RedBlackTreeNode<T>* pnode) const { return pnode->left; } template<class T> RedBlackTreeNode<T>* RedBlackTree<T>::get_right(RedBlackTreeNode<T>* pnode) const { return pnode->right; } template<class T> int RedBlackTree<T>::get_color(RedBlackTreeNode<T>* pnode) const { return pnode->color; } template<class T> void RedBlackTree<T>::set_color(RedBlackTreeNode<T>* pnode,const int& color) { pnode->color=color; } template<class T> RedBlackTreeNode<T>* RedBlackTree<T>::get_successor(RedBlackTreeNode<T>* pnode) const { if(pnode->right!=NIL) return get_minimum(pnode->right); else { RedBlackTreeNode<T>* parentnode=get_parent(pnode); while(parentnode!=NIL&&pnode==parentnode->right) { pnode=parentnode; parentnode=get_parent(pnode); } return parentnode; } } template<class T> RedBlackTreeNode<T>* RedBlackTree<T>::get_predecessor(RedBlackTreeNode<T>* pnode) const { if(pnode->left!=NIL) return get_maximum(pnode->left); else { RedBlackTreeNode<T>* parentnode=get_parent(pnode); while(parentnode!=NIL&&pnode==parentnode->left) { pnode=parentnode; parentnode=get_parent(pnode); } return parentnode; } } template<class T> void RedBlackTree<T>::left_rotate(RedBlackTreeNode<T>* pnode) { RedBlackTreeNode<T>* rightnode=get_right(pnode); pnode->right=rightnode->left; if(rightnode->left!=NIL) rightnode->left->parent=pnode; rightnode->parent=pnode->parent; if(pnode->parent==NIL) root=rightnode; else if(pnode==pnode->parent->left) pnode->parent->left=rightnode; else pnode->parent->right=rightnode; rightnode->left=pnode; pnode->parent=rightnode; } template<class T> void RedBlackTree<T>::right_rotate(RedBlackTreeNode<T>* pnode) { RedBlackTreeNode<T>* leftnode=pnode->left; pnode->left=leftnode->right; if(leftnode->right!=NIL) leftnode->right->parent=pnode; leftnode->parent=pnode->parent; if(pnode->parent==NIL) root=leftnode; else if(pnode==pnode->parent->left) pnode->parent->left=leftnode; else pnode->parent->right=leftnode; leftnode->right=pnode; pnode->parent=leftnode; } template<class T> void RedBlackTree<T>::rb_insert_fixup(RedBlackTreeNode<T>* pnode) { RedBlackTreeNode<T>* gpnode,*unclenode;//祖父grandparent结点和叔uncle结点 while(get_color(get_parent(pnode))==RED) { gpnode=get_parent(get_parent(pnode)); if(get_left(gpnode)==get_parent(pnode)) //category A { unclenode=get_right(gpnode); if(get_color(unclenode)==RED) //case 1 { set_color(gpnode,RED); set_color(unclenode,BLACK); set_color(get_parent(pnode),BLACK); pnode=gpnode; } else { if(pnode==get_right(get_parent(pnode))) //case 2 { pnode=get_parent(pnode); left_rotate(pnode); } set_color(get_parent(pnode),BLACK); //case 3 set_color(get_parent(get_parent(pnode)),RED); right_rotate(get_parent(get_parent(pnode))); } }//category A else//category B { unclenode=get_left(gpnode); if(get_color(unclenode)==RED)//case 1 { set_color(gpnode,RED); set_color(unclenode,BLACK); set_color(get_parent(pnode),BLACK); pnode=gpnode; } else { if(pnode==get_left(get_parent(pnode)))//case 2 { pnode=get_parent(pnode); right_rotate(pnode); } set_color(get_parent(pnode),BLACK);//case 3 set_color(get_parent(get_parent(pnode)),RED); right_rotate(get_parent(get_parent(pnode))); } } } root->color=BLACK; } template<class T> void RedBlackTree<T>::rb_delete_fixup(RedBlackTreeNode<T>* pnode) { RedBlackTreeNode<T>* brothernode; while(pnode!=root&&get_color(pnode)==BLACK) { if(get_left(get_parent(pnode))==pnode) //category A { brothernode=get_right(get_parent(pnode)); if(get_color(brothernode)==RED) //case f1 { set_color(brothernode,BLACK); set_color(get_parent(pnode),RED); left_rotate(get_parent(pnode)); brothernode=get_right(get_parent(pnode)); } if(get_color(get_left(brothernode))==BLACK&&get_color(get_right(brothernode))==BLACK) //case 2 { set_color(brothernode,RED); pnode=get_parent(pnode); } else { if(get_color(get_right(brothernode))==BLACK) //case 3 { set_color(get_left(brothernode),BLACK); set_color(brothernode,RED); right_rotate(brothernode); brothernode=get_right(get_parent(pnode)); } set_color(brothernode,get_color(get_parent(pnode))); //case 4 set_color(get_parent(pnode),BLACK); set_color(get_right(brothernode),BLACK); left_rotate(get_parent(pnode)); pnode=root; } }//category A else //category B { brothernode=get_left(get_parent(pnode)); if(get_color(brothernode)==RED)//case 1 { set_color(brothernode,BLACK); set_color(get_parent(pnode),RED); right_rotate(get_parent(pnode)); brothernode=get_left(get_parent(pnode)); } if(get_color(get_left(brothernode))==BLACK&&get_color(get_right(brothernode))==BLACK)//case 2 { set_color(brothernode,RED); pnode=get_parent(pnode); } else { if(get_color(get_left(brothernode))==BLACK)//case 3 { set_color(get_right(brothernode),BLACK); set_color(brothernode,RED); left_rotate(brothernode); brothernode=get_left(get_parent(pnode)); } set_color(brothernode,get_color(get_parent(pnode)));//case 4 set_color(get_parent(pnode),BLACK); set_color(get_left(brothernode),BLACK); right_rotate(get_parent(pnode)); pnode=root; } } } pnode->color=BLACK; } template<class T> int RedBlackTree<T>::insert_key(const T& key) { RedBlackTreeNode<T>* newnode=new RedBlackTreeNode<T>(); newnode->key=key; newnode->color=RED; newnode->parent=NIL; newnode->left=NIL; newnode->right=NIL; if(NULL==root) { root=newnode; } else { RedBlackTreeNode<T>* tmpnode=root; RedBlackTreeNode<T>* parentnode; while(tmpnode!=NIL) { parentnode=tmpnode; if(newnode->key<tmpnode->key) tmpnode=tmpnode->left; else tmpnode=tmpnode->right; } newnode->parent=parentnode; if(newnode->key<parentnode->key) parentnode->left=newnode; else parentnode->right=newnode; } rb_insert_fixup(newnode); return 0; } template<class T> void RedBlackTree<T>::rb_transplant(RedBlackTreeNode<T>* oldnode,RedBlackTreeNode<T>* newnode) { if(get_parent(oldnode)==NIL) root=newnode; else if(oldnode==get_left(get_parent(oldnode))) oldnode->parent->left=newnode; else oldnode->parent->right=newnode; newnode->parent=oldnode->parent; } template<class T> RedBlackTreeNode<T>* RedBlackTree<T>::search_tree_node(const T& k) const { RedBlackTreeNode<T>* ptmpnode=root; while(ptmpnode!=NIL) { if(ptmpnode->key==k) break; else if(ptmpnode->key<k) ptmpnode=ptmpnode->right; else ptmpnode=ptmpnode->left; } return ptmpnode; } template<class T> int RedBlackTree<T>::delete_key(const T& key) { RedBlackTreeNode<T>* pnode=search_tree_node(key); RedBlackTreeNode<T>* replacedNode=pnode; RedBlackTreeNode<T>* fixupNode; int replacedNodeColor=pnode->color; if(pnode!=NIL) { if(pnode->left==NIL) { fixupNode=pnode->right; rb_transplant(pnode,pnode->right); } else if(pnode->right==NIL) { fixupNode=pnode->left; rb_transplant(pnode,pnode->left); } else { RedBlackTreeNode<T>* toReplaceNode=get_minimum(pnode->right); replacedNodeColor=toReplaceNode->color; fixupNode=toReplaceNode->right; if(get_parent(toReplaceNode)==pnode) { fixupNode->parent=toReplaceNode; } else { rb_transplant(toReplaceNode,toReplaceNode->right); toReplaceNode->right=pnode->right; toReplaceNode->right->parent=toReplaceNode; }; rb_transplant(pnode,toReplaceNode); toReplaceNode->left=pnode->left; toReplaceNode->left->parent=toReplaceNode; toReplaceNode->color=pnode->color; } if(replacedNodeColor==BLACK) rb_delete_fixup(fixupNode); return 0; } return -1; } template<class T> void RedBlackTree<T>::make_empty(RedBlackTreeNode<T>* root) { RedBlackTreeNode<T>* pleft=root->left; RedBlackTreeNode<T>* pright=root->right; if(root) { delete root; if(pleft!=NIL) make_empty(pleft); if(pright!=NIL) make_empty(pright); } } template<class T> void RedBlackTree<T>::inorder_tree_walk() const { if(NULL!=root) { stack<RedBlackTreeNode<T>* > tmpStack; RedBlackTreeNode<T>* pnode=root; while(pnode!=NIL||!tmpStack.empty()) { if(pnode!=NIL) { tmpStack.push(pnode); while(pnode->left!=NIL) { pnode=pnode->left; tmpStack.push(pnode); } } pnode=tmpStack.top(); tmpStack.pop(); cout<<pnode->key<<" : "; if(pnode->color==RED) cout<<"RED"<<endl; else cout<<"BLACK"<<endl; pnode=pnode->right; } } } template<class T> int RedBlackTree<T>::get_maximum(T& ret) const { if(root!=NULL) { ret=get_maximum(root)->key; return 0; } return -1; } template<class T> int RedBlackTree<T>::get_minimum(T& ret) const { if(root!=NULL) { ret=get_minimum(root)->key; return 0; } return -1; } template<class T> int RedBlackTree<T>::get_successor(const T& k,T& ret) const { if(NULL!=root) { RedBlackTreeNode<T>* pnode=search_tree_node(k); if(pnode!=NIL) { ret=get_successor(pnode)->key; return 0; } return -1; } return -1; } template<class T> int RedBlackTree<T>::get_predecessor(const T& k,T& ret) const { if(NULL!=root) { RedBlackTreeNode<T>* pnode=search_tree_node(k); if(pnode!=NIL) { ret=get_predecessor(pnode)->key; return 0; } return -1; } return -1; } template<class T> bool RedBlackTree<T>::search_element(const T& key) const { return (NIL!=search_tree_node(key)); } int _tmain(int argc, _TCHAR* argv[]) { RedBlackTree<int> rbtree; int value; rbtree.insert_key(41); rbtree.insert_key(38); rbtree.insert_key(31); rbtree.insert_key(12); rbtree.insert_key(19); rbtree.insert_key(8); cout<<"root is: "<<rbtree.get_root()->key<<endl; cout<<"Inorder walk red black tree:"<<endl; rbtree.inorder_tree_walk(); if(rbtree.get_minimum(value) == 0) cout<<"minmum is: "<<value<<endl; if(rbtree.get_maximum(value) == 0) cout<<"maxmum is: "<<value<<endl; if(rbtree.get_successor(19,value) == 0) cout<<"19 successor is: "<<value<<endl; if(rbtree.get_predecessor(19,value) == 0) cout<<"19 predecessor is: "<<value<<endl; if(rbtree.delete_key(38)==0) cout<<"delete 38 successfully"<<endl; cout<<"root is: "<<rbtree.get_root()->key<<endl; cout<<"Inorder walk red black tree:"<<endl; rbtree.inorder_tree_walk(); return 0; }
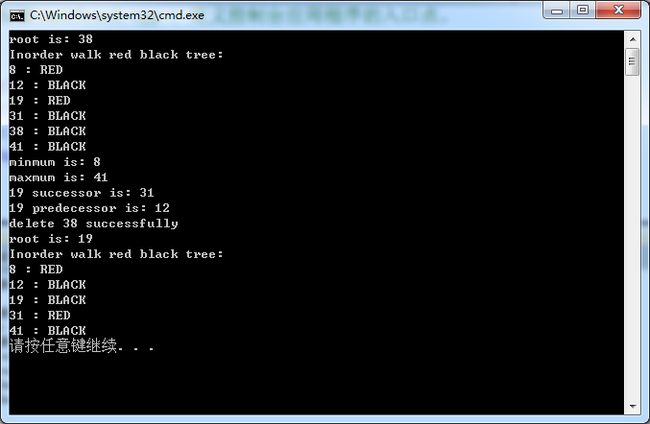
最终结果为:
示例参考自:http://www.cnblogs.com/Anker/archive/2013/01/30/2882773.html