能量不等式的证明
波动方程初值问题能量不等式的证明
Gronwall 不等式
若非负函数 G ( τ ) G(\tau) G(τ) 在 [ 0 , T ] [0,T] [0,T] 上连续可微, G ( 0 ) = 0 G(0)=0 G(0)=0,且对 τ ∈ [ 0 , T ] \tau\in[0,T] τ∈[0,T]满足 d G ( τ ) d τ ≤ C G ( τ ) + F ( τ ) \frac{dG(\tau)}{d\tau}\leq CG(\tau)+F(\tau) dτdG(τ)≤CG(τ)+F(τ) 其中 C C C 为常数且 C > 0 C>0 C>0, F ( τ ) F(\tau) F(τ) 是 [ 0 , T ] [0,T] [0,T] 上不减的非负可积函数,
那么有:
d G ( τ ) d τ ≤ e C τ F ( τ ) \frac{dG(\tau)}{d\tau}\leq e^{C\tau}F(\tau) dτdG(τ)≤eCτF(τ) G ( τ ) ≤ C − 1 ( e C τ − 1 ) F ( τ ) G(\tau)\leq C^{-1}(e^{C\tau}-1)F(\tau) G(τ)≤C−1(eCτ−1)F(τ)
常用的替换技巧
u t u t t = 1 2 ⋅ 2 u t ⋅ u t t = 1 2 ( u t 2 ) t u_{t}u_{tt}=\frac{1}{2}\cdot 2u_{t}\cdot u_{tt}=\frac{1}{2}(u_{t}^2)_t ututt=21⋅2ut⋅utt=21(ut2)t u u t = 1 2 ⋅ 2 u ⋅ u t = 1 2 ( u 2 ) t uu_t=\frac{1}{2}\cdot 2u\cdot u_t =\frac{1}{2}(u^2)_t uut=21⋅2u⋅ut=21(u2)t u u x x = ( u u x ) x − u x 2 = u x 2 + u u x x − u x 2 uu_{xx}=(uu_x)_x-u_x^2=u_x^2+uu_{xx}-u_x^2 uuxx=(uux)x−ux2=ux2+uuxx−ux2 ∵ ( u t u x ) x = u t x u x + u t u x x \because(u_{t}u_{x})_x=u_{tx}u_{x}+u_{t}u_{xx} ∵(utux)x=utxux+utuxx ∴ u t u x x = ( u t u x ) x − u t x u x \therefore u_{t}u_{xx}=(u_{t}u_{x})_x-u_{tx}u_{x} ∴utuxx=(utux)x−utxux
u u u 二阶导函数连续时, u x t = u t x u_{xt}=u_{tx} uxt=utx ∴ u t x u x = 1 2 ( u x 2 ) t = 1 2 ⋅ 2 u x ⋅ u x t = u x u t x \therefore u_{tx}u_{x} = \frac{1}{2}(u_{x}^2)_t=\frac{1}{2}\cdot 2u_{x}\cdot u_{xt}=u_{x}u_{tx} ∴utxux=21(ux2)t=21⋅2ux⋅uxt=uxutx ∴ u t u x x = ( u t u x ) x − 1 2 ( u x 2 ) t \therefore u_{t}u_{xx}=(u_{t}u_{x})_x-\frac{1}{2}(u_{x}^2)_t ∴utuxx=(utux)x−21(ux2)t
能量不等式证明过程
规定 x x x 增长的方向为正方向,而 G r e e n Green Green 公式曲线积分时,组成梯形区域 K τ K_{\tau} Kτ 边界 ∂ K τ \partial K_{\tau} ∂Kτ 的四条线段按照右手法则,只有 Ω 0 \Omega_0 Ω0 这条线段的方向是与右手法则一致,所以有:
∂ K τ = Ω 0 ∪ ( − Γ τ 2 ) ∪ ( − Ω τ ) ∪ ( − Γ τ 1 ) \partial K_{\tau} =\Omega_0\cup(-\Gamma_{\tau_{2}})\cup(-\Omega_{\tau})\cup(-\Gamma_{\tau_{1}}) ∂Kτ=Ω0∪(−Γτ2)∪(−Ωτ)∪(−Γτ1)
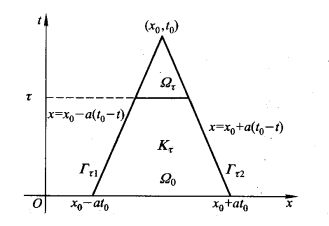
此外,在 ∂ K τ \partial K_{\tau} ∂Kτ 计算曲线积分时,关于 x , t x,t x,t 都积分,但是这两条边 Ω 0 , Ω τ \Omega_0,\Omega_{\tau} Ω0,Ωτ 只在 x x x 方向有增长,而在 t t t 方向无增长,那么这两条线段在计算曲线积分时关于 d t dt dt 的积分项为 0 0 0
待证明的两个不等式:
∫ Ω τ [ u t 2 ( x , τ ) + a 2 u x 2 ( x , τ ) ] d x ≤ M [ ∫ Ω 0 ( ψ 2 + a 2 φ x 2 ) d x + ∬ K τ f 2 ( x , t ) d x d t ] \int_{\Omega_\tau} \left[u_t^2(x, \tau) + a^2 u_x^2(x, \tau)\right] dx \leq M \left[ \int_{\Omega_0} (\psi^2 + a^2 \varphi_x^2) dx + \iint_{K_\tau} f^2(x,t) dxdt \right] ∫Ωτ[ut2(x,τ)+a2ux2(x,τ)]dx≤M[∫Ω0(ψ2+a2φx2)dx+∬Kτf2(x,t)dxdt] ∬ K τ [ u t 2 ( x , t ) + a 2 u x 2 ( x , t ) ] d x d t ≤ M [ ∫ Ω 0 ( ψ 2 + a 2 φ x 2 ) d x + ∬ K τ f 2 ( x , t ) d x d t ] \iint_{K_\tau} \left[u_t^2(x,t) + a^2 u_x^2(x,t)\right] dxdt \leq M \left[ \int_{\Omega_0} (\psi^2 + a^2 \varphi_x^2) dx + \iint_{K_\tau} f^2(x,t) dxdt \right] ∬Kτ[ut2(x,t)+a2ux2(x,t)]dxdt≤M[∫Ω0(ψ2+a2φx2)dx+∬Kτf2(x,t)dxdt]
-
波动方程和能量的关系,在波动方程 ∂ 2 u ∂ t 2 − a 2 ∂ 2 u ∂ x 2 = f \frac{\partial^2 u}{\partial t^2}-a^2\frac{\partial^2 u}{\partial x^2}=f ∂t2∂2u−a2∂x2∂2u=f 两端同乘以 ∂ u ∂ t \frac{\partial u}{\partial t} ∂t∂u 并在区域 K τ K_\tau Kτ 上积分并按照前面的常用替换得: ∬ K τ u t u t t − a 2 u t u x x d x d t = ∬ K τ u t f d x d t \iint_{K_\tau}u_{t}u_{tt}-a^2u_{t}u_{xx}dxdt=\iint_{K_\tau}u_tfdxdt ∬Kτututt−a2utuxxdxdt=∬Kτutfdxdt ∬ K τ 1 2 ( u t 2 + a 2 u x 2 ) t − a 2 ( u t u x ) x d x d t = ∬ K τ u t f d x d t \iint_{K_\tau}\frac{1}{2}(u_{t}^2+a^2u_{x}^2)_t-a^2(u_tu_{x})_{x}dxdt=\iint_{K_\tau}u_tfdxdt ∬Kτ21(ut2+a2ux2)t−a2(utux)xdxdt=∬Kτutfdxdt
-
应用下面这个 Green \text{Green} Green 公式将等式左边也就是时空域上的积分转换为边界上的积分
∬ Ω ∂ P ∂ t + ∂ Q ∂ x d σ = ∮ ∂ Ω − P d x + Q d t \iint_{\Omega}\frac{\partial P}{\partial t}+\frac{\partial Q}{\partial x}d\sigma=\oint_{\partial\Omega}-Pdx+Qdt ∬Ω∂t∂P+∂x∂Qdσ=∮∂Ω−Pdx+Qdt其中 P = 1 2 ( u t 2 + a 2 u x 2 ) P=\frac{1}{2}(u_{t}^2+a^2u_{x}^2) P=21(ut2+a2ux2), Q = − a 2 ( u t u x ) Q=-a^2(u_tu_{x}) Q=−a2(utux),得闭合曲线积分 ∮ ∂ K τ [ − 1 2 ( u t 2 + a 2 u x 2 ) d x − a 2 ( u t u x ) d t ] \oint_{\partial{K_{\tau}}}[-\frac{1}{2}(u_{t}^2+a^2u_{x}^2)dx-a^2(u_tu_{x})dt] ∮∂Kτ[−21(ut2+a2ux2)dx−a2(utux)dt] = − ∮ ∂ K τ a 2 ( u t u x ) d t + 1 2 ( u t 2 + a 2 u x 2 ) d x =-\oint_{\partial{K_{\tau}}}a^2(u_tu_{x})dt+\frac{1}{2}(u_{t}^2+a^2u_{x}^2)dx =−∮∂Kτa2(utux)dt+21(ut2+a2ux2)dx记 a 2 ( u t u x ) d t + 1 2 ( u t 2 + a 2 u x 2 ) d x = □ a^2(u_tu_{x})dt+\frac{1}{2}(u_{t}^2+a^2u_{x}^2)dx = \square a2(utux)dt+21(ut2+a2ux2)dx=□, ∵ ∂ K τ = Ω 0 ∪ ( − Γ τ 2 ) ∪ ( − Ω τ ) ∪ ( − Γ τ 1 ) \because \partial K_{\tau} =\Omega_0\cup(-\Gamma_{\tau_{2}})\cup(-\Omega_{\tau})\cup(-\Gamma_{\tau_{1}})\newline ∵∂Kτ=Ω0∪(−Γτ2)∪(−Ωτ)∪(−Γτ1)
∴ − ∮ ∂ K τ a 2 ( u t u x ) d t + 1 2 ( u t 2 + a 2 u x 2 ) d x \therefore -\oint_{\partial{K_{\tau}}}a^2(u_tu_{x})dt+\frac{1}{2}(u_{t}^2+a^2u_{x}^2)dx ∴−∮∂Kτa2(utux)dt+21(ut2+a2ux2)dx = − [ ∫ Ω 0 □ − ∫ Ω τ □ − ∫ Γ τ 1 □ − ∫ Γ τ 2 □ ] =-[\int_{\Omega_0}\square-\int_{\Omega_{\tau}}\square-\int_{\Gamma_{\tau_{1}}}\square-\int_{\Gamma_{\tau_{2}}}\square]\newline =−[∫Ω0□−∫Ωτ□−∫Γτ1□−∫Γτ2□]
Ω 0 , Ω τ \Omega_0,\Omega_{\tau} Ω0,Ωτ 只在 x x x 方向有增长,而在 t t t 方向无增长,那么这两条线段在计算曲线积分时关于 d t dt dt 的积分项为 0 0 0,可得 − ∮ ∂ K τ a 2 ( u t u x ) d t + 1 2 ( u t 2 + a 2 u x 2 ) d x -\oint_{\partial{K_{\tau}}}a^2(u_tu_{x})dt+\frac{1}{2}(u_{t}^2+a^2u_{x}^2)dx −∮∂Kτa2(utux)dt+21(ut2+a2ux2)dx = ∫ Γ τ 1 ∪ Γ τ 2 a 2 ( u t u x ) d t + 1 2 ( u t 2 + a 2 u x 2 ) d x − ∫ Ω 0 1 2 ( u t 2 + a 2 u x 2 ) d x + ∫ Ω τ 1 2 ( u t 2 + a 2 u x 2 ) d x =\int_{\Gamma_{\tau_{1}}\cup\Gamma_{\tau_{2}}}a^2(u_tu_{x})dt+\frac{1}{2}(u_{t}^2+a^2u_{x}^2)dx-\int_{\Omega_0}\frac{1}{2}(u_{t}^2+a^2u_{x}^2)dx+\int_{\Omega_\tau}\frac{1}{2}(u_{t}^2+a^2u_{x}^2)dx =∫Γτ1∪Γτ2a2(utux)dt+21(ut2+a2ux2)dx−∫Ω021(ut2+a2ux2)dx+∫Ωτ21(ut2+a2ux2)dx记上面等式的三项分别为 J 1 , J 2 , J 3 J_1,J_2,J_3 J1,J2,J3,即: J 1 = ∫ Γ τ 1 ∪ Γ τ 2 a 2 ( u t u x ) d t + 1 2 ( u t 2 + a 2 u x 2 ) d x J_1=\int_{\Gamma_{\tau_{1}}\cup\Gamma_{\tau_{2}}}a^2(u_tu_{x})dt+\frac{1}{2}(u_{t}^2+a^2u_{x}^2)dx J1=∫Γτ1∪Γτ2a2(utux)dt+21(ut2+a2ux2)dx J 2 = − ∫ Ω 0 1 2 ( u t 2 + a 2 u x 2 ) d x J_2=-\int_{\Omega_0}\frac{1}{2}(u_{t}^2+a^2u_{x}^2)dx J2=−∫Ω021(ut2+a2ux2)dx J 3 = ∫ Ω τ 1 2 ( u t 2 + a 2 u x 2 ) d x J_3=\int_{\Omega_\tau}\frac{1}{2}(u_{t}^2+a^2u_{x}^2)dx J3=∫Ωτ21(ut2+a2ux2)dx -
应用下面 d x dx dx 和 d t dt dt 的关系,将 J 1 J_1 J1 统一为只关于 d t dt dt 的积分
Γ τ 1 : d x = a d t \Gamma_{\tau_{1}}:dx=adt Γτ1:dx=adt Γ τ 2 : d x = − a d t \Gamma_{\tau_{2}}:dx=-adt Γτ2:dx=−adt即 J 1 = ∫ Γ τ 1 a 2 ( u t u x ) d t + 1 2 a ( u t 2 + a 2 u x 2 ) d t + ∫ Γ τ 2 a 2 ( u t u x ) d t − 1 2 a ( u t 2 + a 2 u x 2 ) d t J_1=\int_{\Gamma_{\tau_{1}}}a^2(u_tu_{x})dt+\frac{1}{2}a(u_{t}^2+a^2u_{x}^2)dt+\int_{\Gamma_{\tau_{2}}}a^2(u_tu_{x})dt-\frac{1}{2}a(u_{t}^2+a^2u_{x}^2)dt\newline J1=∫Γτ1a2(utux)dt+21a(ut2+a2ux2)dt+∫Γτ2a2(utux)dt−21a(ut2+a2ux2)dt
= ∫ Γ τ 1 a 2 ( 2 a u t u x + u t 2 + a 2 u x 2 ) d t + ∫ Γ τ 1 a 2 ( 2 a u t u x − u t 2 − a 2 u x 2 ) d t =\int_{\Gamma_{\tau_{1}}}\frac{a}{2}(2au_tu_{x}+u_{t}^2+a^2u_{x}^2)dt+\int_{\Gamma_{\tau_{1}}}\frac{a}{2}(2au_tu_{x}-u_{t}^2-a^2u_{x}^2)dt\newline =∫Γτ12a(2autux+ut2+a2ux2)dt+∫Γτ12a(2autux−ut2−a2ux2)dt
利用完全平方公式得 J 1 = ∫ Γ τ 1 a 2 ( u t + a u x ) 2 d t − ∫ Γ τ 2 a 2 ( u t − a u x ) 2 d t J_1=\int_{\Gamma_{\tau_{1}}}\frac{a}{2}(u_t+au_x)^2dt-\int_{\Gamma_{\tau_{2}}}\frac{a}{2}(u_t-au_x)^2dt J1=∫Γτ12a(ut+aux)2dt−∫Γτ22a(ut−aux)2dt因为在 Γ τ 1 \Gamma_{\tau_{1}} Γτ1 线段上规定的正方向是 t t t 增长的方向,而 Γ τ 2 \Gamma_{\tau_{2}} Γτ2 上相反,所以 t t t 的积分限分别是 0 0 0 到 τ \tau τ 和 τ \tau τ 到 0 0 0 ,也即 J 1 = ∫ 0 τ a 2 ( u t + a u x ) 2 d t − ∫ τ 0 a 2 ( u t − a u x ) 2 d t ≥ 0 J_1=\int_{0}^{\tau}\frac{a}{2}(u_t+au_x)^2dt-\int_{\tau}^0\frac{a}{2}(u_t-au_x)^2dt\geq0 J1=∫0τ2a(ut+aux)2dt−∫τ02a(ut−aux)2dt≥0第一项平方项且积分下限小于上限故其积分非负,而第二项是平方项在积分下限大于上限加上前面的负号,故也是非负,所以 J 1 ≥ 0 J_1\geq0 J1≥0 -
把 J 1 , J 2 , J 3 J_1,J_2,J_3 J1,J2,J3 写回来,根据 J 1 ≥ 0 J_1\geq0 J1≥0 构造不等关系 J 1 + J 2 + J 3 = ∬ K τ u t f d x d t J_1+J_2+J_3=\iint_{K_{\tau}}u_{t}fdxdt J1+J2+J3=∬Kτutfdxdt ∵ J 1 ≥ 0 \because J_1\geq0 ∵J1≥0 ∴ J 3 ≤ J 1 + J 3 = J 1 + J 2 + J 3 − J 2 = ∬ K τ u t f d x d t − J 2 \therefore J_3\leq J_1+J_3=J_1+J_2+J_3-J_2=\iint_{K_{\tau}}u_{t}fdxdt-J_2 ∴J3≤J1+J3=J1+J2+J3−J2=∬Kτutfdxdt−J2,也即 ∫ Ω τ 1 2 ( u t 2 + a 2 u x 2 ) d x ≤ ∬ K τ u t f d x d t + ∫ Ω 0 1 2 ( u t 2 + a 2 u x 2 ) d x \int_{\Omega_\tau}\frac{1}{2}(u_{t}^2+a^2u_{x}^2)dx\leq \iint_{K_{\tau}}u_{t}fdxdt+\int_{\Omega_0}\frac{1}{2}(u_{t}^2+a^2u_{x}^2)dx ∫Ωτ21(ut2+a2ux2)dx≤∬Kτutfdxdt+∫Ω021(ut2+a2ux2)dx两边同乘 2 2 2 且 Ω 0 \Omega_0 Ω0 是 t = 0 t=0 t=0 的线段,而 t = 0 t=0 t=0 时, u t ( x , 0 ) = ψ , u x ( x , 0 ) = φ x u_t(x,0)=\psi,u_x(x,0)=\varphi_{x} ut(x,0)=ψ,ux(x,0)=φx即
∫ Ω τ ( u t 2 + a 2 u x 2 ) d x ≤ ∬ K τ 2 u t f d x d t + ∫ Ω 0 ( ψ 2 + a 2 φ x 2 ) d x \int_{\Omega_\tau}(u_{t}^2+a^2u_{x}^2)dx\leq \iint_{K_{\tau}}2u_{t}fdxdt+\int_{\Omega_0}(\psi^2+a^2\varphi_{x}^2)dx ∫Ωτ(ut2+a2ux2)dx≤∬Kτ2utfdxdt+∫Ω0(ψ2+a2φx2)dx对上面不等式右边 ∬ K τ 2 u t f d x d t \iint_{K_{\tau}}2u_{t}fdxdt ∬Kτ2utfdxdt 这一项应用 C a u c h y Cauchy Cauchy 不等式 2 a b ≤ a 2 + b 2 2ab\leq a^2+b^2 2ab≤a2+b2 得
∫ Ω τ ( u t 2 + a 2 u x 2 ) d x ≤ ∬ K τ u t 2 + f 2 d x d t + ∫ Ω 0 ( ψ 2 + a 2 φ x 2 ) d x \int_{\Omega_\tau}(u_{t}^2+a^2u_{x}^2)dx\leq \iint_{K_{\tau}}u_{t}^2+f^2dxdt+\int_{\Omega_0}(\psi^2+a^2\varphi_{x}^2)dx ∫Ωτ(ut2+a2ux2)dx≤∬Kτut2+f2dxdt+∫Ω0(ψ2+a2φx2)dx此时,对比要证明的不等式 ∫ Ω τ ( u t 2 + a 2 u x 2 ) d x ≤ ∬ K τ f 2 d x d t + ∫ Ω 0 ( ψ 2 + a 2 φ x 2 ) d x \int_{\Omega_\tau}(u_{t}^2+a^2u_{x}^2)dx\leq \iint_{K_{\tau}}f^2dxdt+\int_{\Omega_0}(\psi^2+a^2\varphi_{x}^2)dx ∫Ωτ(ut2+a2ux2)dx≤∬Kτf2dxdt+∫Ω0(ψ2+a2φx2)dx发现只是右端多了一项 ∬ K τ u t 2 d x d t \iint_{K_{\tau}}u_{t}^2dxdt ∬Kτut2dxdt -
利用 G r o n w a l l Gronwall Gronwall 不等式将该项消去
\newline
令 G ( τ ) = ∬ K τ ( u t 2 + a 2 u x 2 ) d x d t = ∫ 0 τ ∫ x 0 − a ( t 0 − t ) x 0 + a ( t 0 − t ) ( u t 2 + a 2 u x 2 ) d x d t G(\tau)=\iint_{K_{\tau}}(u_{t}^2+a^2u_{x}^2)dxdt=\int_{0}^{\tau}\int_{x_0-a(t_0-t)}^{x_0+a(t_0-t)}(u_{t}^2+a^2u_{x}^2)dxdt\newline G(τ)=∬Kτ(ut2+a2ux2)dxdt=∫0τ∫x0−a(t0−t)x0+a(t0−t)(ut2+a2ux2)dxdt
则 d G ( τ ) d τ = ∫ Ω τ ( u t 2 + a 2 u x 2 ) d x \frac{dG(\tau)}{d\tau}=\int_{\Omega_\tau}(u_{t}^2+a^2u_{x}^2)dx dτdG(τ)=∫Ωτ(ut2+a2ux2)dx 是待证明不等式的左端
\newline
令 F ( τ ) = ∬ K τ f 2 d x d t + ∫ Ω 0 ( ψ 2 + a 2 φ x 2 ) d x F(\tau)=\iint_{K_{\tau}}f^2dxdt+\int_{\Omega_0}(\psi^2+a^2\varphi_{x}^2)dx F(τ)=∬Kτf2dxdt+∫Ω0(ψ2+a2φx2)dx
\newline
给 ∫ Ω τ ( u t 2 + a 2 u x 2 ) d x ≤ ∬ K τ u t 2 + f 2 d x d t + ∫ Ω 0 ( ψ 2 + a 2 φ x 2 ) d x \int_{\Omega_\tau}(u_{t}^2+a^2u_{x}^2)dx\leq \iint_{K_{\tau}}u_{t}^2+f^2dxdt+\int_{\Omega_0}(\psi^2+a^2\varphi_{x}^2)dx ∫Ωτ(ut2+a2ux2)dx≤∬Kτut2+f2dxdt+∫Ω0(ψ2+a2φx2)dx 右边添加 ∬ K τ a 2 u x 2 d x d t \iint_{K_{\tau}}a^2u_{x}^2dxdt ∬Kτa2ux2dxdt,则 ∫ Ω τ ( u t 2 + a 2 u x 2 ) d x ≤ ∬ K τ u t 2 + a 2 u x 2 + f 2 d x d t + ∫ Ω 0 ( ψ 2 + a 2 φ x 2 ) d x \int_{\Omega_\tau}(u_{t}^2+a^2u_{x}^2)dx\leq \iint_{K_{\tau}}u_{t}^2+a^2u_{x}^2+f^2dxdt+\int_{\Omega_0}(\psi^2+a^2\varphi_{x}^2)dx ∫Ωτ(ut2+a2ux2)dx≤∬Kτut2+a2ux2+f2dxdt+∫Ω0(ψ2+a2φx2)dx那么此时该不等式满足 G r o n w a l l Gronwall Gronwall 不等式的前提条件 d G ( τ ) d τ ≤ C G ( τ ) + F ( τ ) \frac{dG(\tau)}{d\tau}\leq CG(\tau)+F(\tau) dτdG(τ)≤CG(τ)+F(τ)此时 C = 1 C=1 C=1,那么由 G r o n w a l l Gronwall Gronwall 不等式的两个结论,可分别得到如下两个能量不等式,其中 M = e τ M=e^\tau M=eτ ∫ Ω τ [ u t 2 ( x , τ ) + a 2 u x 2 ( x , τ ) ] d x ≤ M [ ∫ Ω 0 ( ψ 2 + a 2 φ x 2 ) d x + ∬ K τ f 2 ( x , t ) d x d t ] \int_{\Omega_\tau} \left[u_t^2(x, \tau) + a^2 u_x^2(x, \tau)\right] dx \leq M \left[ \int_{\Omega_0} (\psi^2 + a^2 \varphi_x^2) dx + \iint_{K_\tau} f^2(x,t) dxdt \right] ∫Ωτ[ut2(x,τ)+a2ux2(x,τ)]dx≤M[∫Ω0(ψ2+a2φx2)dx+∬Kτf2(x,t)dxdt] ∬ K τ [ u t 2 ( x , t ) + a 2 u x 2 ( x , t ) ] d x d t ≤ M [ ∫ Ω 0 ( ψ 2 + a 2 φ x 2 ) d x + ∬ K τ f 2 ( x , t ) d x d t ] \iint_{K_\tau} \left[u_t^2(x,t) + a^2 u_x^2(x,t)\right] dxdt \leq M \left[ \int_{\Omega_0} (\psi^2 + a^2 \varphi_x^2) dx + \iint_{K_\tau} f^2(x,t) dxdt \right] ∬Kτ[ut2(x,t)+a2ux2(x,t)]dxdt≤M[∫Ω0(ψ2+a2φx2)dx+∬Kτf2(x,t)dxdt]
波动方程混合问题能量不等式的证明
待证明的两个不等式:
∫ 0 l [ u t 2 ( x , τ ) + a 2 u x 2 ( x , τ ) ] d x ≤ M [ ∫ 0 l ( ψ 2 + a 2 φ x 2 ) d x + ∬ Q τ f 2 d x d t ] \int_{0}^{l} \left[u_t^2(x, \tau) + a^2 u_x^2(x, \tau)\right] dx \leq M \left[ \int_{0}^{l} (\psi^2 + a^2 \varphi_x^2) dx + \iint_{Q_\tau} f^2 dxdt \right] ∫0l[ut2(x,τ)+a2ux2(x,τ)]dx≤M[∫0l(ψ2+a2φx2)dx+∬Qτf2dxdt] ∬ Q τ ( u t 2 + a 2 u x 2 ) d x d t ≤ M [ ∫ 0 l ( ψ 2 + a 2 φ x 2 ) d x + ∬ Q τ f 2 d x d t ] \iint_{Q_\tau} \left(u_t^2 + a^2 u_x^2\right) dxdt \leq M \left[ \int_{0}^{l} (\psi^2 + a^2 \varphi_x^2) dx + \iint_{Q_\tau} f^2 dxdt \right] ∬Qτ(ut2+a2ux2)dxdt≤M[∫0l(ψ2+a2φx2)dx+∬Qτf2dxdt]
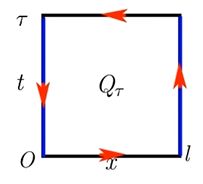
二维区域的情况下,这里可以不用 G r e e n Green Green 公式将面积分转为线积分,可以直接按照二重积分展开。
-
在波动方程 u t t − a 2 u x x = f u_{tt}-a^2u_{xx}=f utt−a2uxx=f 两端同乘 u t u_t ut 并在区域 Q τ = ( 0 , l ) × ( 0 , τ ) Q_\tau=(0,l)\times(0,\tau) Qτ=(0,l)×(0,τ) 上积分
\newline
∬ Q τ u t u t t − a 2 u t u x x d x d t = ∬ Q τ u t f d x d t \iint_{Q_\tau}u_{t}u_{tt}-a^2u_{t}u_{xx}dxdt=\iint_{Q_\tau}u_tf dxdt ∬Qτututt−a2utuxxdxdt=∬Qτutfdxdt
\newline
利用常用的替换技巧 u t u t t = 1 2 ⋅ 2 u t ⋅ u t t = 1 2 ( u t 2 ) t u_{t}u_{tt}=\frac{1}{2}\cdot 2u_{t}\cdot u_{tt}=\frac{1}{2}(u_{t}^2)_t ututt=21⋅2ut⋅utt=21(ut2)t u t u x x = ( u t u x ) x − 1 2 ( u x 2 ) t u_{t}u_{xx}=(u_{t}u_{x})_x-\frac{1}{2}(u_{x}^2)_t utuxx=(utux)x−21(ux2)t得 ∬ Q τ 1 2 ( u t 2 ) t + 1 2 a 2 ( u x 2 ) t − ( a 2 u t u x ) x d x d t \iint_{Q_\tau}\frac{1}{2}(u_{t}^2)_t+\frac{1}{2}a^2(u_{x}^2)_t-(a^2u_tu_x)_xdxdt ∬Qτ21(ut2)t+21a2(ux2)t−(a2utux)xdxdt,这里用二重积分展开 ∬ Q τ 1 2 ( u t 2 ) t + 1 2 a 2 ( u x 2 ) t − ( a 2 u t u x ) x d x d t \iint_{Q_\tau}\frac{1}{2}(u_{t}^2)_t+\frac{1}{2}a^2(u_{x}^2)_t-(a^2u_tu_x)_xdxdt ∬Qτ21(ut2)t+21a2(ux2)t−(a2utux)xdxdt = ∫ 0 τ ∫ 0 l [ ( 1 2 u t 2 + 1 2 a 2 u x 2 ) t − ( a 2 u t u x ) x ] d x d t =\int_{0}^{\tau}\int_{0}^{l}[(\frac{1}{2}u_{t}^2+\frac{1}{2}a^2u_{x}^2)_t-(a^2u_tu_x)_x]dxdt =∫0τ∫0l[(21ut2+21a2ux2)t−(a2utux)x]dxdt = ∫ 0 l 1 2 u t 2 ( x , τ ) + 1 2 a 2 u x 2 ( x , τ ) d x − ∫ 0 l 1 2 u t 2 ( x , 0 ) + 1 2 a 2 u x 2 ( x , 0 ) d x − ∫ 0 τ a 2 u t ( l , t ) u x ( l , t ) d t + ∫ 0 τ a 2 u t ( 0 , t ) u x ( 0 , t ) d t =\int_{0}^{l}\frac{1}{2}u_{t}^{2}(x,\tau)+\frac{1}{2}a^2u_{x}^{2}(x,\tau)dx-\int_{0}^{l}\frac{1}{2}u_{t}^{2}(x,0)+\frac{1}{2}a^2u_{x}^{2}(x,0)dx-\int_{0}^{\tau}a^2u_{t}(l,t)u_{x}(l,t)dt+\int_{0}^{\tau}a^2u_{t}(0,t)u_{x}(0,t)dt =∫0l21ut2(x,τ)+21a2ux2(x,τ)dx−∫0l21ut2(x,0)+21a2ux2(x,0)dx−∫0τa2ut(l,t)ux(l,t)dt+∫0τa2ut(0,t)ux(0,t)dt -
根据初始条件和齐次边界条件替换上面表达式
\newline
初始条件: u t ( x , 0 ) = ψ ( x ) u_t(x,0)=\psi(x) ut(x,0)=ψ(x) u x ( x , 0 ) = φ x ( x ) u_x(x,0)=\varphi_x(x) ux(x,0)=φx(x)边界条件: u ( 0 , t ) = 0 u(0,t)=0 u(0,t)=0 u ( l , t ) = 0 u(l,t)=0 u(l,t)=0即杆的两端是固定的,也即速度为 0 0 0
u t ( l , t ) = u t ( 0 , t ) = 0 u_t(l,t)=u_t(0,t)=0 ut(l,t)=ut(0,t)=0 带入 1. 1. 1. 得到的等式并两边同乘 2 2 2 得 = ∫ 0 l u t 2 ( x , τ ) + a 2 u x 2 ( x , τ ) d x = ∫ 0 l ψ 2 + a 2 φ x 2 d x + 2 ∫ 0 τ ∫ 0 l u t f d x d t =\int_{0}^{l}u_{t}^{2}(x,\tau)+a^2u_{x}^{2}(x,\tau)dx=\int_{0}^{l}\psi^2+a^2\varphi_{x}^{2}dx+2\int_{0}^{\tau}\int_{0}^{l}u_tfdxdt =∫0lut2(x,τ)+a2ux2(x,τ)dx=∫0lψ2+a2φx2dx+2∫0τ∫0lutfdxdt对等式右边应用 C a u c h y Cauchy Cauchy 不等式以及添加非负项 ∫ 0 τ ∫ 0 l a 2 u x 2 d x d t \int_{0}^{\tau}\int_{0}^{l}a^2u_{x}^2dxdt ∫0τ∫0la2ux2dxdt 得 ∫ 0 l u t 2 ( x , τ ) + a 2 u x 2 ( x , τ ) d x ≤ ∫ 0 l ψ 2 + a 2 φ x 2 d x + ∫ 0 τ ∫ 0 l f 2 d x d t + ∫ 0 τ ∫ 0 l u t 2 + a 2 u x 2 d x d t \int_{0}^{l}u_{t}^{2}(x,\tau)+a^2u_{x}^{2}(x,\tau)dx\leq \int_{0}^{l}\psi^2+a^2\varphi_{x}^{2}dx+\int_{0}^{\tau}\int_{0}^{l}f^2dxdt+\int_{0}^{\tau}\int_{0}^{l}u_{t}^2+a^2u_{x}^2dxdt ∫0lut2(x,τ)+a2ux2(x,τ)dx≤∫0lψ2+a2φx2dx+∫0τ∫0lf2dxdt+∫0τ∫0lut2+a2ux2dxdt -
应用 G r o n w a l l Gronwall Gronwall 不等式
\newline
令 G ( τ ) = ∫ 0 τ ∫ 0 l u t 2 + a 2 u x 2 d x d t G(\tau) = \int_{0}^{\tau}\int_{0}^{l}u_{t}^2+a^2u_{x}^2dxdt G(τ)=∫0τ∫0lut2+a2ux2dxdt
\newline
F ( τ ) = ∫ 0 l ψ 2 + a 2 φ x 2 d x + ∫ 0 τ ∫ 0 l f 2 d x d t F(\tau)=\int_{0}^{l}\psi^2+a^2\varphi_{x}^{2}dx+\int_{0}^{\tau}\int_{0}^{l}f^2dxdt F(τ)=∫0lψ2+a2φx2dx+∫0τ∫0lf2dxdt
\newline
那么 d G ( τ ) d τ = ∫ 0 l u t 2 ( x , τ ) + a 2 u x 2 ( x , τ ) d x \frac{dG(\tau)}{d\tau}=\int_{0}^{l}u_{t}^{2}(x,\tau)+a^2u_{x}^{2}(x,\tau)dx dτdG(τ)=∫0lut2(x,τ)+a2ux2(x,τ)dx
\newline
将 G ( τ ) , F ( τ ) , d G ( τ ) d τ G(\tau),F(\tau),\frac{dG(\tau)}{d\tau} G(τ),F(τ),dτdG(τ) 带入 G r o n w a l l Gronwall Gronwall 不等式的两个结论即得到待证不等式,其中 C = 1 C=1 C=1