Dynamic Time Warping 动态时间规整算法

Dynamic Time Warping（DTW）是一种衡量两个时间序列之间的相似度的方法，主要应用在语音识别领域来识别两段语音是否表示同一个单词。

1. DTW方法原理

在时间序列中，需要比较相似性的两段时间序列的长度可能并不相等，在语音识别领域表现为不同人的语速不同。而且同一个单词内的不同音素的发音速度也不同，比如有的人会把“A”这个音拖得很长，或者把“i”发的很短。另外，不同时间序列可能仅仅存在时间轴上的位移，亦即在还原位移的情况下，两个时间序列是一致的。在这些复杂情况下，使用传统的欧几里得距离无法有效地求的两个时间序列之间的距离（或者相似性）。

DTW通过把时间序列进行延伸和缩短，来计算两个时间序列性之间的相似性：

如上图所示，上下两条实线代表两个时间序列，时间序列之间的虚线代表两个时间序列之间的相似的点。DTW使用所有这些相似点之间的距离的和，称之为归整路径距离(Warp Path Distance)来衡量两个时间序列之间的相似性。

2. DTW计算方法：

令要计算相似度的两个时间序列为X和Y，长度分别为|X|和|Y|。

归整路径(Warp Path)

归整路径的形式为W=w₁,w₂,...,w_K，其中Max(|X|,|Y|)<=K<=|X|+|Y|。

w_k的形式为(i,j)，其中i表示的是X中的i坐标，j表示的是Y中的j坐标。

归整路径W必须从w1=(1,1)开始，到wK=(|X|,|Y|)结尾，以保证X和Y中的每个坐标都在W中出现。

另外，W中w(i,j)的i和j必须是单调增加的，以保证图1中的虚线不会相交，所谓单调增加是指：

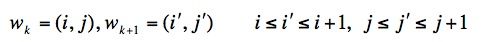
最后要得到的归整路径是距离最短的一个归整路径：

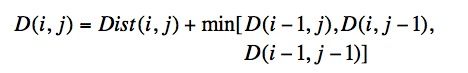
最后求得的归整路径距离为D(|X|,|Y|)，使用动态规划来进行求解：

上图为代价矩阵(Cost Matrix) D，D(i,j)表示长度为i和j的两个时间序列之间的归整路径距离。

3. DTW实现：

matlab代码：

function dist = dtw(t,r)

n = size(t,1);

m = size(r,1);

% 帧匹配距离矩阵

d = zeros(n,m);

for i = 1:n

    for j = 1:m

        d(i,j) = sum((t(i,:)-r(j,:)).^2);

    end

end

% 累积距离矩阵

D = ones(n,m) * realmax;

D(1,1) = d(1,1);

% 动态规划

for i = 2:n

    for j = 1:m

        D1 = D(i-1,j);

        if j>1

            D2 = D(i-1,j-1);

        else

            D2 = realmax;

        end

        if j>2

            D3 = D(i-1,j-2);

        else

            D3 = realmax;

        end

        D(i,j) = d(i,j) + min([D1,D2,D3]);

    end

end

dist = D(n,m);

C++实现：

dtwrecoge.h

View Code

/***dtwrecoge.h*********************************************************************/

#ifndef dtwrecoge_h

#define dtwrecoge_h



#include<stdio.h>

#include<math.h>



#define DTWMAXNUM 2000

#define MAX(a,b) ((a)>(b)?(a):(b))

#define MIN(a,b) ((a)<(b)?(a):(b))

#define ABS(a) ((a)>0?(a):(-(a)))

#define DTWVERYBIG 100000000.0



/*****************************************************************************/

/* DTWDistance，求两个数组之间的匹配距离

/* A,B分别为第一第二个数组，I，J为其数组长度，r为匹配窗口的大小

/* r的大小一般取为数组长度的1/10到1/30

/* 返回两个数组之间的匹配距离,如果返回－1.0，表明数组长度太大了

/*****************************************************************************/

double DTWDistanceFun(double *A,int I,double *B,int J,int r);



/*****************************************************************************/

/* DTWTemplate，进行建立模板的工作

/* 其中A为已经建立好的模板，我们在以后加入训练样本的时候，

/* 以已建立好的模板作为第一个参数，I为模板的长度，在这个模板中不再改变

/* B为新加入的训练样本，J为B的长度，turn为训练的次数，在第一次

/* 用两个数组建立模板时，r为1，这是出于权值的考虑

/* temp保存匹配最新训练后的模板，建议temp[DTWMAXNUM]，函数返回最新训练后模板的长度

/* 如果函数返回-1，表明训练样本之间距离过大，需要重新选择训练样本，

/* tt为样本之间距离的阈值，自行定义

/*****************************************************************************/

int DTWTemplate(double *A,int I,double *B,int J,double *temp,int turn,double tt,double *rltdistance);



#endif

 dtwrecoge.cpp

View Code

/*dtwrecoge.cpp**************************************************************/



#include "dtwrecoge.h"

double distance[DTWMAXNUM][DTWMAXNUM]; /*保存距离*/

double dtwpath[DTWMAXNUM][DTWMAXNUM]; /*保存路径*/



/*****************************************************************************/

/* DTWDistance，求两个数组之间的匹配距离

/* A,B分别为第一第二个数组，I，J为其数组长度，r为匹配窗口的大小



/* r的大小一般取为数组长度的1/10到1/30

/* 返回两个数组之间的匹配距离,如果返回－1.0，表明数组长度太大了

/*****************************************************************************/

double DTWDistanceFun(double *A,int I,double *B,int J,int r)

{

    int i,j;

    double dist;

    int istart,imax;

    int r2=r+ABS(I-J);/*匹配距离*/

    double g1,g2,g3;

    int pathsig=1;/*路径的标志*/



    /*检查参数的有效性*/

    if(I>DTWMAXNUM||J>DTWMAXNUM){

        //printf("Too big number\n");

        return -1.0;

    }

    

    /*进行一些必要的初始化*/

    for(i=0;i<I;i++){

        for(j=0;j<J;j++){

            dtwpath[i][j]=0;

            distance[i][j]=DTWVERYBIG;

        }

    }

    

    /*动态规划求最小距离*/

    /*这里我采用的路径是 -------

                              . |

                            .   |

                          .     |

                        .       |

     */

    distance[0][0]=(double)2*ABS(A[0]-B[0]);

    for(i=1;i<=r2;i++){

        distance[i][0]=distance[i-1][0]+ABS(A[i]-B[0]);

    }

    for(j=1;j<=r2;j++){

        distance[0][j]=distance[0][j-1]+ABS(A[0]-B[j]);

    }

    

    for(j=1;j<J;j++){

        istart=j-r2;

        if(j<=r2)

            istart=1;

        imax=j+r2;

        if(imax>=I)

            imax=I-1;

        

        for(i=istart;i<=imax;i++){

            g1=distance[i-1][j]+ABS(A[i]-B[j]);

            g2=distance[i-1][j-1]+2*ABS(A[i]-B[j]);

            g3=distance[i][j-1]+ABS(A[i]-B[j]);

            g2=MIN(g1,g2);

            g3=MIN(g2,g3);

            distance[i][j]=g3;

        }

    }

        

    dist=distance[I-1][J-1]/((double)(I+J));

    return dist;

}/*end DTWDistance*/



/*****************************************************************************/

/* DTWTemplate，进行建立模板的工作

/* 其中A为已经建立好的模板，我们在以后加入训练样本的时候，

/* 以已建立好的模板作为第一个参数，I为模板的长度，在这个模板中不再改变

/* B为新加入的训练样本，J为B的长度，turn为训练的次数，在第一次

/* 用两个数组建立模板时，r为1，这是出于权值的考虑

/* temp保存匹配最新训练后的模板，建议temp[DTWMAXNUM]，函数返回最新训练后模板的长度

/* 如果函数返回-1，表明训练样本之间距离过大，需要重新选择训练样本，

/* tt为样本之间距离的阀值，自行定义

/* rltdistance保存距离，第一次两个数组建立模板时可以随意赋予一个值，

/* 后面用前一次返回的值赋予该参数

/*****************************************************************************/

int DTWTemplate(double *A,int I,double *B,int J,double *temp,int turn,double tt,double *rltdistance)

{

    double dist;

    int i,j;

    int pathsig=1;

    dist=DTWDistanceFun(A,I,B,J,(int)(I/30));

    if(dist>tt){

        printf("\nSample doesn't match!\n");

        return -1;

    }

        

    if(turn==1)

        *rltdistance=dist;

    else{

        *rltdistance=((*rltdistance)*(turn-1)+dist)/turn;

    }

    /*寻找路径,这里我采用了逆向搜索法*/

    i=I-1;

    j=J-1;

    while(j>=1||i>=1){

        double m;

        if(i>0&&j>0){

            m=MIN(MIN(distance[i-1][j],distance[i-1][j-1]),distance[i][j-1]);

            if(m==distance[i-1][j]){

                dtwpath[i-1][j]=pathsig;

                i--;

            }

            else if(m==distance[i-1][j-1]){

                dtwpath[i-1][j-1]=pathsig;

                i--;

                j--;

            }

            else{

                dtwpath[i][j-1]=pathsig;

                j--;

            }

        }

        else if(i==0){

            dtwpath[0][j-1]=pathsig;

            j--;

        }

        else{/*j==0*/

            dtwpath[i-1][0]=pathsig;

            i--;

        }

    }

    dtwpath[0][0]=pathsig;

    dtwpath[I-1][J-1]=pathsig;

    

    /*建立模板*/

    for(i=0;i<I;i++){

        double ftemp=0.0;

        int ntemp=0;

        for(j=0;j<J;j++){

            if(dtwpath[i][j]==pathsig){

                ftemp+=B[j];

                ntemp++;

            }

        }

        ftemp/=((double)ntemp);

        temp[i]=(A[i]*turn+ftemp)/((double)(turn+1));/*注意这里的权值*/

    }

    

    return I;/*返回模板的长度*/

}//end DTWTemplate

C++代码下载：DTW算法.rar