小波学习之一(单层一维离散小波变换DWT的Mallat算法C++和MATLAB实现)
1 Mallat算法
离散序列的Mallat算法分解公式如下:
其中,H(n)、G(n)分别表示所选取的小波函数对应的低通和高通滤波器的抽头系数序列。
从Mallat算法的分解原理可知,分解后的序列就是原序列与滤波器序列的卷积再进行隔点抽取而来。
离散序列的Mallat算法重构公式如下:
![]()
其中,h(n)、g(n)分别表示所选取的小波函数对应的低通和高通滤波器的抽头系数序列。
2 小波变换实现过程(C/C++)
2.1 小波变换结果序列长度
小波的Mallat算法分解后的序列长度由原序列长SoureLen和滤波器长FilterLen决定。从Mallat算法的分解原理可知,分解后的序列就是原序列与滤波器序列的卷积再进行隔点抽取而来。即分解抽取的结果长度为(SoureLen+FilterLen-1)/2。
2.2 获取滤波器组
对于一些通用的小波函数,简单起见,可以通过Matlab的wfilters(‘wavename’)获取4个滤波器;特殊的小波函数需要自行构造获得。
下面以db1小波函数(Haar小波)为例,其变换与重构滤波器组的结果如下:
//matlab输入获取命令
>> [Lo_D,Hi_D,Lo_R,Hi_R] = wfilters('db1')
//获取的结果
Lo_D =
0.7071 0.7071
Hi_D =
-0.7071 0.7071
Lo_R =
0.7071 0.7071
Hi_R =
0.7071 -0.7071
2.3 信号边界延拓
在Mallat算法中,假定输入序列是无限长的,而实际应用中输入的信号是有限的采样序列,这就会出现信号边界处理问题。对于边界信号的延拓一般有3种方法,即零延拓、对称延拓和周期延拓。
3种延拓方法比较情况如下:
对于正交小波变换来说,前两种延拓方法实现起来比较简单,但重建时会产生边界效应,而且分解的层数越多,产生的边界效应越显著。零延拓方法给人一种跳跃的感觉。至于对称性延拓,由于正交小波滤波器一般都是非对称性的(Haar小波基虽然是正交的,但它是非连续的),重建图象给人一种错位的感觉。相比较而言,只有最后一种延拓方式可以得到比较精确的重建结果,它不仅能保证分解与重建正确计算,而且恢复的质量也好。不过,周期性延拓方法虽然是常用的三种方法中比较好的方法,但会导致信号边缘的非连续性,从而会使得较高频率(子带)层的小波系数很大,即使信号本身相当平滑。从信号压缩的角度看,大的系数是希望避免的。信号的对称延拓可避免边缘的非连续性问题。然而,对称延拓只能和对称的小波滤波器一起适用。如果降低正交性要求,选择双正交小波变换,对称性延拓不失为一种好的方法。周期延拓可适用于任何小波变换,但可能导致输入序列边缘的不连续,使得高频系数较大。而对称延拓则避免了输入序列边界的不连续,是当前广泛采用的一种延拓方法。
下式中给出了最常用的对称延拓表达式。
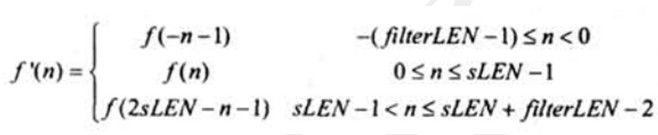
当原序列长sLEN为偶数时延拓后的序列长为sLEN+2*(filterLEN),而原序列长为奇数时则需要在右端再延拓一个元素。注:在Matlab中默认使用了对称延拓。
2.4 小波分解
在db1小波函数下,离散序列的Mallat算法分解公式展开如下:

其它的db小波,不再详述。小波分解C++源码如下。
/**
* @brief 小波变换之分解
* @param sourceData 源数据
* @param dataLen 源数据长度
* @param db 过滤器类型
* @param cA 分解后的近似部分序列-低频部分
* @param cD 分解后的细节部分序列-高频部分
* @return
* 正常则返回分解后序列的数据长度,错误则返回-1
*/
int Wavelet::Dwt(double *sourceData, int dataLen, Filter db, double *cA, double *cD)
{
if(dataLen < 2)
return -1;
if((NULL == sourceData)||(NULL == cA)||(NULL == cD))
return -1;
m_db = db;
int filterLen = m_db.length;
int n,k,p;
int decLen = (dataLen+filterLen-1)/2;
double tmp=0;
cout<<"decLen="<<decLen<<endl;
for(n=0; n<decLen; n++)
{
cA[n] = 0;
cD[n] = 0;
for(k=0; k<filterLen; k++)
{
p = 2*n-k; // 感谢网友onetrain指正,此处由p = 2*n-k+1改为p = 2*n-k,解决小波重构后边界异常问题--2013.3.29 by hmm
// 信号边沿对称延拓
if((p<0)&&(p>=-filterLen+1))
tmp = sourceData[-p-1];
else if((p>dataLen-1)&&(p<=dataLen+filterLen-2))
tmp = sourceData[2*dataLen-p-1];
else if((p>=0)&&(p<dataLen-1))
tmp = sourceData[p];
else
tmp = 0;
// 分解后的近似部分序列-低频部分
cA[n] += m_db.lowFilterDec[k]*tmp;
// 分解后的细节部分序列-高频部分
cD[n] += m_db.highFilterDec[k]*tmp;
}
}
return decLen;
}
2.5 小波重构
/**
* @brief 小波变换之重构
* @param cA 分解后的近似部分序列-低频部分
* @param cD 分解后的细节部分序列-高频部分
* @param cALength 输入数据长度
* @param db 过滤器类型
* @param recData 重构后输出的数据
*/
void Wavelet::Idwt(double *cA, double *cD, int cALength, Filter db, double *recData)
{
if((NULL == cA)||(NULL == cD)||(NULL == recData))
return;
m_db = db;
int filterLen = m_db.length;
int n,k,p;
int recLen = 2*cALength-filterLen+1;
cout<<"recLen="<<recLen<<endl;
for(n=0; n<recLen; n++)
{
recData[n] = 0;
for(k=0; k<cALength; k++)
{
p = n-2*k+filterLen-1;
// 信号重构
if((p>=0)&&(p<filterLen))
{
recData[n] += m_db.lowFilterRec[p]*cA[k] + m_db.highFilterRec[p]*cD[k];
//cout<<"recData["<<n<<"]="<<recData[n]<<endl;
}
}
}
}
2.6 c++实现结果

3 小波变换实现(MATLAB)
使用matlab小波工具箱实现db4的情况如下。
1、MatlabDB4.m文件内容。
%加载txt数据示例
s=importdata('data2.txt'); %load data2.txt;
subplot(521);plot(s); %画出原始信号的波形图
title('原始信号');
[cA,cD]=dwt(s,'db4'); %采用db4小波并对信号进行一维离散小波分解。
y=idwt(cA,cD,'db4'); %一维离散小波反变换
subplot(522);
plot(cA); %画出波形图
title('MATLAB低频部分dwt-cA');
subplot(523);
plot(cD); %画出波形图
title('MATLAB高频部分dwt-cD');
subplot(524);
plot(y); %画出波形图
title('MATLAB重构idwt');
2、波形图如下。
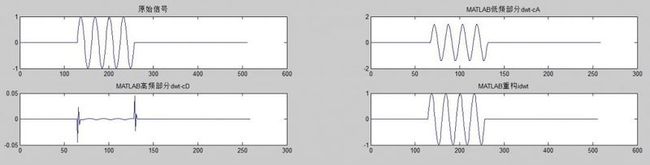
4 小结
在此,采用C++实现了dbN系列小波的单层一维离散小波变换,通过对比db4小波变换发现(笔者也同样对比验证了db1-db3),C++实现效果和Matlab效果完全一样。通过这一过程,可以很好地帮助理解小波变换的Mallat算法原理,并将C++代码快速应用到工程实践,同时对MATLAB小波工具箱的实现细节也有更深入的理解。相关文献表明,C++代码实现的DWT算法比Matlab小波工具箱dwt方法效率更高。
注:对小波变换见识还不深,有问题者,欢迎提出讨论交流,对源码细节感兴趣的tx,可以到如下链接下载。
http://download.csdn.net/detail/v_hyx/5113111
