图,网路与邻接矩阵
用一个二维数组存放顶点间关系(边或弧)的数据,这个二维数组称为邻接矩阵。邻接矩阵又分为有向图邻接矩阵和无向图邻接矩阵。对无向图而言,邻接矩阵一定是对称的,而且对角线一定为零(在此仅讨论无向简单图),有向图则不一定如此。在无向图中,任一顶点i的度为第i列所有元素的和,在有向图中顶点i的出度为第i行所有元素的和,而入度为第i列所有元素的和。用邻接矩阵法表示图共需要n^2个空间,由于无向图的邻接矩阵一定具有对称关系,所以扣除对角线为零外,仅需要存储上三角形或下三角形的数据即可,因此仅需要n(n-1)/2个空间。
1.图的邻接矩阵表示法
在图的邻接矩阵表示法中:
① 用邻接矩阵表示顶点间的相邻关系
② 用一个顺序表来存储顶点信息
2.图的邻接矩阵(Adacency Matrix)
设G=(V,E)是具有n个顶点的图,则G的邻接矩阵是具有如下性质的n阶方阵:

【例】下图中无向图G 5 和有向图G 6 的邻接矩阵分别为A l 和A 2 。

3.网络的邻接矩阵
若G是网络,则邻接矩阵可定义为:
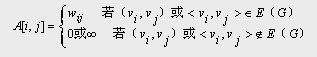
其中:
w ij 表示边上的权值;
∞表示一个计算机允许的、大于所有边上权值的数。
【例】下面带权图的两种邻接矩阵分别为A 3 和A 4 。

4.图的邻接矩阵存储结构形式说明
#define MaxVertexNum l00 //最大顶点数,应由用户定义
typedef char VertexType; //顶点类型应由用户定义
typedef int EdgeType; //边上的权值类型应由用户定义
typedef struct{
VextexType vexs[MaxVertexNum] //顶点表
EdeType edges[MaxVertexNum][MaxVertexNum];
//邻接矩阵,可看作边表
int n,e; //图中当前的顶点数和边数
}MGragh;
注意:
① 在简单应用中,可直接用二维数组作为图的邻接矩阵(顶点表及顶点数等均可省略)。
② 当邻接矩阵中的元素仅表示相应的边是否存在时,EdgeTyPe可定义为值为0和1的枚举类型。
③ 无向图的邻接矩阵是对称矩阵,对规模特大的邻接矩阵可压缩存储。
④ 邻接矩阵表示法的空间复杂度S(n)=0(n 2 )。
5.建立无向网络的算法。
void CreateMGraph(MGraph *G)
{//建立无向网的邻接矩阵表示
int i,j,k,w;
scanf("%d%d",&G->n,&G->e); //输入顶点数和边数
for(i=0;i<G->n;i++) //读人顶点信息,建立顶点表
G->vexs[i]=getchar();
for(i=0;i<G->n;i++)
for(j=0;j<G->n;j++)
G->edges[i][j]=0; //邻接矩阵初始化
for(k=0;k<G->e;k++){//读入e条边,建立邻接矩阵
scanf("%d%d%d",&i,&j,&w);//输入边(v i ,v j )上的权w
G->edges[i][j]=w;
G->edges[j][i]=w;
}
}//CreateMGraph
该算法的执行时间是0(n+n 2 +e)。由于e<n 2 ,算法的时间复杂度是0(n 2 )。