对弈类游戏的人工智能(1)--评估函数+博弈树算法
前言:
对弈类游戏的智能算法, 网上资料颇多, 大同小异. 我写这篇文章, 并非想做互联网的搬运工. 而是想对当年的经典<<PC游戏编程(人机博弈)>>表达敬意, 另一方面, 也想对自己当年的游戏编程人生做下回顾.
这边我们以黑白棋游戏为例, 从博弈和学习两方面来阐述游戏AI的编写要点. 本文侧重于讲述博弈(评估函数+博弈算法).

博弈:
以前看围棋比赛, 常有人评价棋手水平高: 大局观强(评估局面好), 算路精准(计算步数深, 实战效果好). 他山之石可以攻玉, 对弈类游戏的AI本质上也是在评估局面, 博弈深度这两点上做足了文章.
(一)评估函数:
让我们先来谈谈局面评估, 那如何从程序的角度去合理评估游戏的局势呢?
首先局面的好坏, 需要综合考虑多个因素(权重不同, 不同阶段重要性的变化), 其次因素影响力需转化为数值来衡量.
为了简化模型, 我们引入评估函数G(s), s为当前的局面, G(s)为当前局面的评估值.
G(s) = a1 * f1(s) + a2 * f2(s) + ... + an * fn(s)
注: fi(s)为某个评估因素的得分, ai为某个评估因素的权重比
评估函数G(s)的引入, 为游戏AI的智能引入了数学模型, 也是一切的基础.
回到黑白棋游戏本身, 依据经验选定如下特征评估因素:
1).地势估值表
黑白棋和围棋一样, 也遵守着"金角银边烂肚皮"的定律, 四个角的地势值非常大, 其次是四条边. 因此我们再给8*8地图点分配地势值时, 大体满足角边重, 中腹轻的模式.
potential_enegy(s) = ∑ pe[x, y] {map[x,y] is occupied, 8>x>=0, 8>y>=0}
注: potential_enegy(s) 为地势评估函数, pe[x,y] 为地势估值矩阵, map[x,y]是游戏地图本身.
2).行动力
基于这样的假设: 在某局面中, 选择多, 则灵活主动, 而选择少, 则往往陷入被动. 因此选择多少, 就成为了评估局面好坏的参考因素了. 于是我们把面对某一局面, 可以落子的个数, 称之为行动力.
3).稳定子
所谓稳定子, 是指无论如何, 都不可能被翻覆的子, 最简单的稳定子就是4个角点, 稳定值越多, 获胜的几率就越大.
有了这些评估因素后, 再赋予一定的权重系数, 评估函数就比较完善了. 此时游戏的AI也基本构建完毕, 其棋力能击败初学者, 应该不成问题.
但此时的AI很脆弱, 看似每步都选择最佳落子, 却很容易落入陷阱. 这就是贪心算法, 导致的局部最优陷阱. 如何破这个局呢? 期待王者到来: 博弈树.
(二)博弈树:
博弈树本质就是极大极小的搜索过程,相关资料可参考博文: "极大极小博弈树".
极大极小的算法, 分支繁多而冗余, 于是引入alpha+beta剪枝做优化, 它可以快速裁剪不必要的搜索分支, 提高搜索效率.
关于这块, 就不再具体展开, 参见如下博文: A*算法/博弈树, 机器博弈中的基本搜索算法;
alpha+beta剪枝的极大极小过程示意图:
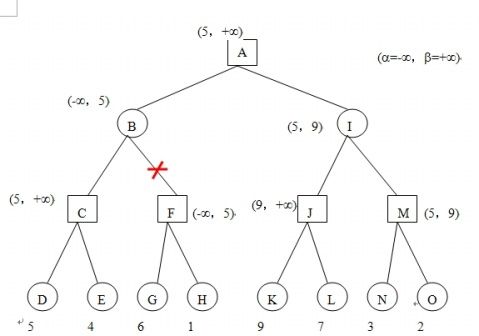
负极大值算法伪码:
// 负极大值算法
int negamax(GameState S, int depth, int alpha, int beta) {
// 游戏是否结束 || 探索的递归深度是否到边界
if ( gameover(S) || depth == 0 ) {
return evaluation(S);
}
// 遍历每一个候选步
foreach ( move in candidate list ) {
S' = makemove(S);
value = -negamax(S', depth - 1, -beta, -alpha);
unmakemove(S')
if ( value > alpha ) {
// alpha + beta剪枝点
if ( value >= beta ) {
return beta;
}
alpha = value;
}
}
return alpha;
}
展望:
有了评估函数和博弈树后, 其游戏AI有了飞跃的进步, 但一山更有一山高, 我们是否能够更进一步呢?
对于评估函数, 我们当前的策略是基于经验, 选择评估因素和权重分配. 能否用机器学习的方法,自动实现因素(特征)选择, 权重系数合理分配呢?
而对于博弈算法本身, 是否还有优化的地方? 搜索深度和搜索分支的广度如何权衡?
最重要的如何设置进阶的AI难度, 增强用户的体验?
因篇幅受限, 决定放到下一篇博文中.
总结:
为何选择黑白棋作为对弈类游戏AI解说的对象, 一方面游戏规则简单, 另一方面其评估模型容易构建, 且其搜索分支少+搜索深度深, 这些对快速实现并理解博弈游戏的AI核心算法有非常大的帮助. 该博文主要讲述了评估函数和博弈树的原理和优化. 下文讲着重讲述下 博弈游戏的AI如何学习, 以及性能优化的进阶篇.
写在最后:
如果你觉得这篇文章对你有帮助, 请小小打赏下. 其实我想试试, 看看写博客能否给自己带来一点小小的收益. 无论多少, 都是对楼主一种由衷的肯定.
