Construct a tree from Inorder and Level order traversals

Given inorder and level-order traversals of a Binary Tree, construct the Binary Tree. Following is an example to illustrate the problem.

BinaryTree

Input: Two arrays that represent Inorder and level order traversals of a Binary Tree
in[]    = {4, 8, 10, 12, 14, 20, 22};
level[] = {20, 8, 22, 4, 12, 10, 14};

Output: Construct the tree represented by the two arrays. For the above two arrays, the constructed tree is shown in the diagram.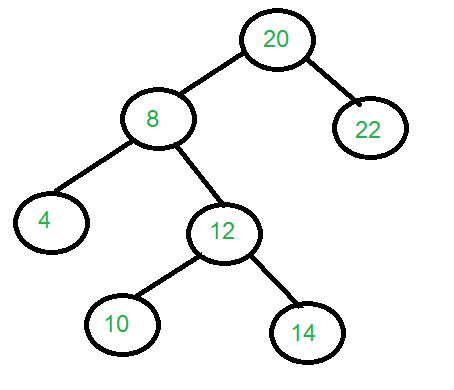

geeksforgeeks的做法是，每次以in和level数组去构建以level[0]为根结点的树。生成下一次level结点的开销是O(n)，所以整个时间复杂度是O(n^2)。

我的做法是：

1. 先计算出所有点的层序号。基于这个规律，如果两个元素在同一层，那么后面的数在中序遍历的顺序中，必然也是处于后面；如果后面的数在中序遍历中处于前面，那么必然是处于下一层。O(n)可以做到，但是需要先对两个数组作索引。

2. 从最后一层开始，每一层的左结点，是在inorder序列中，在它左边的连续序列（该序列必须保证层数比它大）中第一个层数=它的层数+1的数。右结点同理。查找左右结点的开销需要O(n)。

所以最终可以做到$O(n^2)$。

 1 struct TreeNode {

 2     int val;

 3     TreeNode *left, *right;

 4     TreeNode(int v): val(v), left(NULL), right(NULL) {}

 5 };

 6 

 7 void print(TreeNode *root) {

 8     if (root == NULL) {

 9         cout << "NULL ";

10     } else {

11         cout << root->val << " ";

12         print(root->left);

13         print(root->right);

14     }

15 }

16 

17 struct Indices {

18     int inOrderIndex;

19     int levelOrderIndex;

20     int level;

21 };

22 

23 int main(int argc, char** argv) {

24     vector<int> inOrder = {4, 8, 10, 12, 14, 20, 22};

25     vector<int> levelOrder = {20, 8, 22, 4, 12, 10, 14};

26 

27     // build indices

28     unordered_map<int, Indices> indices;

29     for (int i = 0; i < inOrder.size(); ++i) {

30         if (indices.count(inOrder[i]) <= 0) {

31             indices[inOrder[i]] = {i, 0, 0};

32         } else {

33             indices[inOrder[i]].inOrderIndex = i;

34         }

35         if (indices.count(levelOrder[i]) <= 0) {

36             indices[levelOrder[i]] = {0, i, 0};

37         } else {

38             indices[levelOrder[i]].levelOrderIndex = i;

39         }

40     }

41 

42     // get level no. for each number

43     int level = 0;

44     for (int i = 1; i < levelOrder.size(); ++i) {

45         if (indices[levelOrder[i]].inOrderIndex < indices[levelOrder[i - 1]].inOrderIndex) {

46             ++level;

47         }     

48         indices[levelOrder[i]].level = level;    

49     }

50 

51     unordered_map<int, TreeNode*> nodes;

52     for (int i = levelOrder.size() - 1; i >= 0; --i) {

53         nodes[levelOrder[i]] = new TreeNode(levelOrder[i]);

54         int index = indices[levelOrder[i]].inOrderIndex;

55         for (int j = index - 1; j >= 0 && indices[inOrder[j]].level > indices[inOrder[index]].level; --j) {

56             if (indices[inOrder[j]].level == indices[inOrder[index]].level + 1) {

57                 nodes[levelOrder[i]]->left = nodes[inOrder[j]];

58                 break;

59             }

60         }

61         for (int j = index + 1; j < levelOrder.size() && indices[inOrder[j]].level > indices[inOrder[index]].level; ++j) {

62             if (indices[inOrder[j]].level == indices[inOrder[index]].level + 1) {

63                 nodes[levelOrder[i]]->right = nodes[inOrder[j]];

64                 break;

65             }

66         }

67     }

68     print(nodes[levelOrder[0]]);

69     cout << endl;

70     return 0;

71 }