canvas游戏开发学习之七：变形

状态的保存和恢复 Saving and restoring state

在了解变形之前，我先介绍一下两个在你开始绘制复杂图形就必不可少的方法。

save()
restore()

save 和 restore 方法是用来保存和恢复 canvas 状态的，都没有参数。Canvas 的状态就是当前画面应用的所有样式和变形的一个快照。Canvas 状态是以堆(stack)的方式保存的，每一次调用 save 方法，当前的状态就会被推入堆中保存起来。你可以调用任意多次 save 方法。每一次调用 restore 方法，上一个保存的状态就从堆中弹出，所有设定都恢复。

save 和 restore 的应用例子

我们尝试用这个连续矩形的例子来描述 canvas 的状态堆是如何工作的。

第一步是用默认设置画一个大四方形，然后保存一下状态。改变填充颜色画第二个小一点的蓝色四方形，然后再保存一下状态。再次改变填充颜色绘制更小一点的半透明的白色四方形。到目前为止所做的动作和前面章节的都很类似。不过一旦我们调用 restore，状态堆中最后的状态会弹出，并恢复所有设置。如果不是之前用 save 保存了状态，那么我们就需要手动改变设置来回到前一个状态，这个对于两三个属性的时候还是适用的，一旦多了，我们的代码将会猛涨。当第二次调用 restore 时，已经恢复到最初的状态，因此最后是再一次绘制出一个黑色的四方形。

 function draw() {  
     var ctx = document.getElementById('canvas').getContext('2d');  
      
     ctx.fillRect(0,0,150,150);   // Draw a rectangle with default settings  
     ctx.save();                  // Save the default state  
      
     ctx.fillStyle = '#09F'       // Make changes to the settings  
     ctx.fillRect(15,15,120,120); // Draw a rectangle with new settings  
      
     ctx.save();                  // Save the current state  
     ctx.fillStyle = '#FFF'       // Make changes to the settings  
     ctx.globalAlpha = 0.5;      
     ctx.fillRect(30,30,90,90);   // Draw a rectangle with new settings  
     
     ctx.restore();               // Restore previous state  
     ctx.fillRect(45,45,60,60);   // Draw a rectangle with restored settings  
     
     ctx.restore();               // Restore original state  
     ctx.fillRect(60,60,30,30);   // Draw a rectangle with restored settings  
 }  

移动 Translating

我们先介绍 translate 方法，它用来移动 canvas 和它的原点到一个不同的位置。

translate(x, y)

translate 方法接受两个参数。x 是左右偏移量，y 是上下偏移量，如下图所示。

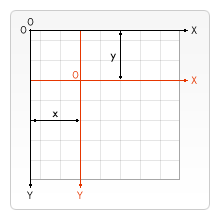
在做变形之前先保存状态是一个良好的习惯。大多数情况下，调用 restore 方法比手动恢复原先的状态要简单得多。又，如果你是在一个循环中做位移但没有保存和恢复 canvas 的状态，很可能到最后会发现怎么有些东西不见了，那是因为它很可能已经超出 canvas 范围以外了。

translate 的例子

这个例子显示了一些移动 canvas 原点的好处。我创建了一个 drawSpirograph 方法用来绘制螺旋（spirograph）图案，那是围绕原点绘制出来的。如果不使用 translate 方法，那么只能看见其中的四分之一。translate 同时让我可以任意放置这些图案，而不需要在 spirograph 方法中手工调整坐标值，既好理解也方便使用。我在 draw 方法中调用 drawSpirograph 方法 9 次，用了 2 层循环。每一次循环，先移动 canvas ，画螺旋图案，然后恢复早原始状态。

   function draw() {  
      var ctx = document.getElementById('canvas').getContext('2d');  
      ctx.fillRect(0,0,300,300);  
      for (var i=0;i<3;i++) {  
        for (var j=0;j<3;j++) {  
          ctx.save();  
          ctx.strokeStyle = "#9CFF00";  
          ctx.translate(50+j*100,50+i*100);  
          drawSpirograph(ctx,20*(j+2)/(j+1),-8*(i+3)/(i+1),10);  
         ctx.restore();  
        }  
      }  
   }  
  function drawSpirograph(ctx,R,r,O){  
     var x1 = R-O;  
     var y1 = 0;  
     var i  = 1;  
     ctx.beginPath();  
     ctx.moveTo(x1,y1);  
     do {  
       if (i>20000) break;  
       var x2 = (R+r)*Math.cos(i*Math.PI/72) - (r+O)*Math.cos(((R+r)/r)*(i*Math.PI/72))  
       var y2 = (R+r)*Math.sin(i*Math.PI/72) - (r+O)*Math.sin(((R+r)/r)*(i*Math.PI/72))  
       ctx.lineTo(x2,y2);  
       x1 = x2;  
       y1 = y2;  
       i++;  
     } while (x2 != R-O && y2 != 0 );  
     ctx.stroke();  
  }  

旋转 Rotating

第二个介绍 rotate 方法，它用于以原点为中心旋转 canvas。

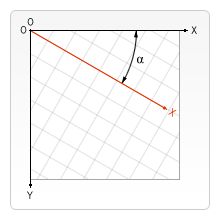
rotate(angle)

这个方法只接受一个参数：旋转的角度(angle)，它是顺时针方向的，以弧度为单位的值。旋转的中心点始终是 canvas 的原点，如果要改变它，我们需要用到 translate 方法。

rotate 的例子

在这个例子里，见下图，我用 rotate 方法来画圆并构成圆形图案。当然你也可以分别计算出 x 和 y 坐标(x = r*Math.cos(a); y = r*Math.sin(a))。这里无论用什么方法都无所谓的，因为我们画的是圆。计算坐标的结果只是旋转圆心位置，而不是圆本身。即使用 rotate 旋转两者，那些圆看上去还是一样的，不管它们绕中心旋转有多远。这里我们又用到了两层循环。第一层循环决定环的数量，第二层循环决定每环有多少个点。每环开始之前，我都保存一下 canvas 的状态，这样恢复起来方便。每次画圆点，我都以一定夹角来旋转 canvas，而这个夹角则是由环上的圆点数目的决定的。最里层的环有 6 个圆点，这样，每次旋转的夹角就是 360/6 = 60 度。往外每一环的圆点数目是里面一环的 2 倍，那么每次旋转的夹角随之减半。

   function draw() {  
      var ctx = document.getElementById('canvas').getContext('2d');  
      ctx.translate(75,75);  
      
      for (var i=1;i<6;i++){ // Loop through rings (from inside to out)  
        ctx.save();  
        ctx.fillStyle = 'rgb('+(51*i)+','+(255-51*i)+',255)';  
      
        for (var j=0;j<i*6;j++){ // draw individual dots  
         ctx.rotate(Math.PI*2/(i*6));  
         ctx.beginPath();  
         ctx.arc(0,i*12.5,5,0,Math.PI*2,true);  
         ctx.fill();  
       }       
       ctx.restore();  
     }  
  }  

缩放 Scaling

接着是缩放。我们用它来增减图形在 canvas 中的像素数目，对形状，位图进行缩小或者放大。

scale(x, y)

scale 方法接受两个参数。x,y 分别是横轴和纵轴的缩放因子，它们都必须是正值。值比 1.0 小表示缩小，比 1.0 大则表示放大，值为 1.0 时什么效果都没有。默认情况下，canvas 的 1 单位就是 1 个像素。举例说，如果我们设置缩放因子是 0.5，1 个单位就变成对应 0.5 个像素，这样绘制出来的形状就会是原先的一半。同理，设置为 2.0 时，1 个单位就对应变成了 2 像素，绘制的结果就是图形放大了 2 倍。

scale 的例子

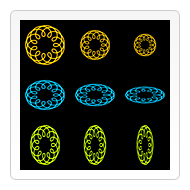
这最后的例子里，我再次启用前面曾经用过的 spirograph 方法，来画 9 个图形，分别赋予不同的缩放因子。左上角的图形是未经缩放的。黄色图案从左到右应用了统一的缩放因子（x 和 y 参数值是一致的）。看下面的代码，你可以发现，我在画第二第三个图案时 scale 了两次，中间没有 restore canvas 的状态，因此第三个图案的缩放因子其实是 0.75 × 0.75 = 0.5625。第二行蓝色图案堆垂直方向应用了不统一的缩放因子，每个图形 x 方向上的缩放因子都是 1.0，意味着不缩放，而 y 方向缩放因子是 0.75，得出来的结果是，图案被依次压扁了。原来的圆形图案变成了椭圆，如果细心观察，还可以发现在垂直方向上的线宽也减少了。第三行的绿色图案与第二行类似，只是缩放限定在横轴方向上了。

function draw() {
  var ctx = document.getElementById('canvas').getContext('2d');
  ctx.strokeStyle = "#fc0";
  ctx.lineWidth = 1.5;
  ctx.fillRect(0,0,300,300);

  // Uniform scaling
  ctx.save()
  ctx.translate(50,50);
  drawSpirograph(ctx,22,6,5);

  ctx.translate(100,0);
  ctx.scale(0.75,0.75);
  drawSpirograph(ctx,22,6,5);

  ctx.translate(133.333,0);
  ctx.scale(0.75,0.75);
  drawSpirograph(ctx,22,6,5);
  ctx.restore();

  // Non uniform scaling (y direction)
  ctx.strokeStyle = "#0cf";
  ctx.save()
  ctx.translate(50,150);
  ctx.scale(1,0.75);
  drawSpirograph(ctx,22,6,5);

  ctx.translate(100,0);
  ctx.scale(1,0.75);
  drawSpirograph(ctx,22,6,5);

  ctx.translate(100,0);
  ctx.scale(1,0.75);
  drawSpirograph(ctx,22,6,5);
  ctx.restore();

  // Non uniform scaling (x direction)
  ctx.strokeStyle = "#cf0";
  ctx.save()
  ctx.translate(50,250);
  ctx.scale(0.75,1);
  drawSpirograph(ctx,22,6,5);

  ctx.translate(133.333,0);
  ctx.scale(0.75,1);
  drawSpirograph(ctx,22,6,5);

  ctx.translate(177.777,0);
  ctx.scale(0.75,1);
  drawSpirograph(ctx,22,6,5);
  ctx.restore();
  
}
function drawSpirograph(ctx,R,r,O){
  var x1 = R-O;
  var y1 = 0;
  var i  = 1;
  ctx.beginPath();
  ctx.moveTo(x1,y1);
  do {
    if (i>20000) break;
    var x2 = (R+r)*Math.cos(i*Math.PI/72) - (r+O)*Math.cos(((R+r)/r)*(i*Math.PI/72))
    var y2 = (R+r)*Math.sin(i*Math.PI/72) - (r+O)*Math.sin(((R+r)/r)*(i*Math.PI/72))
    ctx.lineTo(x2,y2);
    x1 = x2;
    y1 = y2;
    i++;
  } while (x2 != R-O && y2 != 0 );
  ctx.stroke();
}

变形 Transforms

最后一个方法是允许直接对变形矩阵作修改。

m11     m21     dx
m12     m22     dy
0       0       1

setTransform(m11, m12, m21, m22, dx, dy)

这个方法必须重置当前的变形矩阵为单位矩阵，然后以相同的参数调用 transform 方法。如果任意一个参数是无限大，那么变形矩阵也必须被标记为无限大，否则会抛出异常。

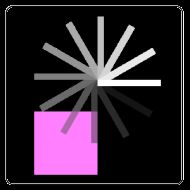
transform / setTransform 的例子

   function draw() {  
      var canvas = document.getElementById("canvas");  
      var ctx = canvas.getContext("2d");  
      
      var sin = Math.sin(Math.PI/6);  
      var cos = Math.cos(Math.PI/6);  
      ctx.translate(200, 200);  
      var c = 0;  
      for (var i=0; i <= 12; i++) {  
        c = Math.floor(255 / 12 * i);  
        ctx.fillStyle = "rgb(" + c + "," + c + "," + c + ")";  
        ctx.fillRect(0, 0, 100, 10);  
        ctx.transform(cos, sin, -sin, cos, 0, 0);  
      }  
       
     ctx.setTransform(-1, 0, 0, 1, 200, 200);  
     ctx.fillStyle = "rgba(255, 128, 255, 0.5)";  
     ctx.fillRect(0, 50, 100, 100);  
   }