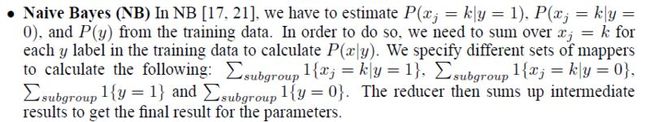常见数据挖掘算法的Map-Reduce策略(1)

       大数据这个名词是被炒得越来越火了，各种大数据技术层出不穷，做数据挖掘的也跟着火了一把，呵呵，现今机器学习算法常见的并行实现方式：MPI，Map-Reduce计算框架，GPU方面，graphlab的图并行，Spark计算框架，本文讲讲一些机器学习算法的map-reduce并行策略，尽管有些算法确实不适合map-reduce计算，但是掌握一些并行思想策略总归不是件坏事，大家如果对某个算法有更好的并行策略，也请多多指教，欢迎大家交流，OK，下面先从一个最基本的均值、方差的并行开始。

 

均值、方差的map-reduce

       一堆数字的均值、方差公式，相信都很清楚，具体怎么设计map跟reduce函数呢，可以先从计算公式出发，假设有n个数字，分别是a1,a2....an，那么  均值m=(a1+a2+...an) / n，方差 s= [(a1-m)^2+ (a2-m)^2+....+ (an-m)^2] / n

把方差公式展开来S=[(a1^2+.....an^2)+m^m*n-2*m*(a1+a2+....an) ] / n，根据这个我们可以把map端的输入设定为（key,a1），输出设定为(1,(n1,sum1,var1))，n1表示每个worker所计算的数字的个数，sum1是这些数字的和(例如a1+a2+a3...)，var1是这些数字的平方和(例如a1^2+a2^2+...)

       reduce端接收到这些信息后紧接着把所有输入的n1,n2....相加得到n,把sum1,sum2...相加得到sum，那么均值m=sum/n， 把var1,var2...相加得到var，那么最后的方差S=(var+m^2*n-2*m*sum)/n，reduce输出(1,(m,S))。

算法代码是基于mrjob的实现(https://pythonhosted.org/mrjob/，机器学习实战第十五章)

 1 from mrjob.job import MRJob
 2 
 3  
 4 
 5 class MRmean(MRJob):
 6 
 7     def __init__(self, *args, **kwargs):
 8 
 9         super(MRmean, self).__init__(*args, **kwargs)
10 
11         self.inCount = 0
12 
13         self.inSum = 0
14 
15         self.inSqSum = 0
16 
17     
18 
19     def map(self, key, val): #needs exactly 2 arguments
20 
21         if False: yield
22 
23         inVal = float(val)
24 
25         self.inCount += 1
26 
27         self.inSum += inVal #每个元素之和
28 
29         self.inSqSum += inVal*inVal #求每个元素的平方
30 
31         
32 
33     def map_final(self):
34 
35         mn = self.inSum/self.inCount
36 
37         mnSq =self.inSqSum/self.inCount
38         yield (1, [self.inCount, mn, mnSq]) #map的输出，不过这里的mn=sum1/mn,mnsq=var1/mn
39 
40  
41 
42     def reduce(self, key, packedValues):
43 
44         cumVal=0.0; cumSumSq=0.0; cumN=0.0
45 
46         for valArr in packedValues: #get values from streamed inputs 解析map端的输出
47 
48             nj = float(valArr[0])
49 
50             cumN += nj
51 
52             cumVal += nj*float(valArr[1])
53 
54             cumSumSq += nj*float(valArr[2])
55 
56         mean = cumVal/cumN
57 
58         var = (cumSumSq - 2*mean*cumVal + cumN*mean*mean)/cumN
59 
60         yield (mean, var) #emit mean and var reduce的输出
61 
62         
63 
64     def steps(self):
65 
66         return ([self.mr(mapper=self.map, mapper_final=self.map_final,\
67 
68                           reducer=self.reduce,)])
69 
70  
71 
72 if __name__ == '__main__':
73 
74     MRmean.run()

 

KNN算法的 map-reduce

       KNN算法作为机器学习里面经典的分类算法，它简单有效，但很粗暴，是一个非参模型(非参并非指算法没有参数，而是说它没有假设底层数据的分布，尽管该算法的有效性要遵循流行/聚类假设)，算法具体的步骤如伪代码所示

 

for i in test_data

    从train_data中找与i样本最相近的K个样本(K是参数，过小引起过拟合，过大引起欠拟合)

    衡量相近的标准有多种(欧氏距离，马氏距离等等)

    把这K个样本的标签出现最多的那个赋予给i

end for

 

       从上面的代码可以看出该算法的计算量也是非常大的，但有个好处是非常适合拆分计算步骤，进行并行处理，具体设计map函数跟reduce函数如下

       map过程：每个worker节点load测试集和部分训练集到本地(当然也可以训练集和部分测试集，但感觉是不是很浪费磁盘？)，map的输入是<key,value>这不废话么。。。具体的key是样本行号，value是样本的属性跟标签, map的输出 <key,list(value)> key是测试样本的行号，value是某个训练样本的标签跟距离 ，具体的map函数伪代码如下

 

for i in test_data

    for j in train_data

         取出j 里面的标签L

         计算i与j的距离D

         context.write(测试样本行号,vector(L,D))

    end for

end for

       

      reduce过程：这个相对就比较简单，对输入键值对，对同一个key的(L,D) 对D进行排序，取出前K个L标签，计算出现最多的那个标签，即为该key的结果。

      总结：上面是一个最基本的knn的map-reduce过程，正常情况下我们reduce的机器一般小于map的机器，如果完全把map的输出，全扔到reduce那边，会造成reduce过程耗时，一个优化的方向就是在map的最后阶段，我们直接对每个key取前K个结果，这样就更合理的利用了计算资源，另外高维情况下，近邻的查找一般用局部敏感哈希算法。

 

朴素贝叶斯算法的 map-reduce   

        朴素贝叶斯算法也是一种经典的分类算法，多用于文本分类 、垃圾邮件的处理，算法简单，计算较快，网络上也有很好的介绍该算法的文章(首推，刘未鹏的平凡而又神奇的贝叶斯)，整个算法的的框架是需要计算4部分，摘选文献1的图片

 

         包括先验概率、每个属性的值在特定类别下的条件概率，下面以一个例子详细说明map-reduce过程，假设数据集如下所示

行号	类别	性别	风强度	温度
01	好	男	强	热
02	坏	女	弱	冷
03	坏	男	中等	热

       首先把属性都进行0/1编码(把属性连续化的一个好方法)，效果如下所示

行号	类别(好)	类别(坏)	性别(男)	性别(女)	风强度(强)	风强度(中等)	风强度(弱)	温度(热)	温度(冷)
01	1	0	1	0	1	0	0	1	0
02	0	1	0	1	0	0	1	0	1
03	0	1	1	0	0	1	0	1	0

         然后 map的输入是<行号，样本 >，在map中作如下操作，对于每条记录record1=[[1,0],[1,0],[1,0,0],[1,0]], record2=[ [0,1],[0,1],[0,0,1],[0,1] ]，record3=[ [0,1],[1,0],[0,1,0],[1,0] ]，然后把标签拆分，把类别作为key,这样map的输出端就是<类别，record1..n>,

       reduce接收到后，进行如下处理对于每个record1 转化成矩阵形式

key=1                   key=0                    key=0

record1=1            record2=1            record3=1

                1,0                         0,1                         1,0

                1,0,0                      0,0,1                      0,1,0

                1,0                         0,1                         1,0

对于每一个类别相同的record相加得到

sum(类别=1)= 1,             sum(类别=0)=2              

                        1,0                                   1,1                         

                        1,0,0                                0,1,1                    

                        1,0                                   1,1    

 

对上面进行归一化,得到

sum(类别=1)= 1,             sum(类别=0)=1              

                        1,0                                   1/2,1/2                         

                        1,0,0                                0,1/2,1/2                    

                        1,0                                   1/2,1/2         

 

最后输出的就是这两个东东了

具体分类的时候，假设一个test样本是（女，强，热）   

P(好 / ( 女，强，热)  ) =P(好)*P(女/好)*P(强/好)*P(热/好)

P(坏 / ( 女，强，热)  ) =P(坏)*P(女/坏)*P(强/坏)*P(热/坏)

       比较上面两个概率的大小就好了，另外文中举的这个例子不太好，出现了 P(女/好)=0，样本足够的情况下是不会的等于零的，即使真出现了0的情况，也可以用拉普拉斯平滑掉就好了。

 

       另外一种思路：map端输出<'好'，1>，<'好,男',1>,<'好,强',1>，< '好,弱',1 >，。。。。，reduce端输出那些key的sum和。总来说跟前一种做法是差不多，都是求各种频数

 

决策树算法的 map-reduce   

        不用说又是一个经典的算法，该算法多简单可解释性强，在各行各业应用都是非常广泛，以它为基础的boosting，forest更是在互联网行业和各大挖掘竞赛上大显身手(GBRT的预估，GBrank的排序，竞赛中也基本是集成成百上千的model)，哎，扯远了，回到本文的话题来，由于决策树是一个迭代性很强的算法，不太适合并行，当然如果训练集达到单机无法承受，并行还是需要滴

        第一种思路：借鉴于上面贝叶斯并行的第二种策略，对于决策树上的每一个节点，都启动一次map-reduce过程，计算各个频数，以求出熵增益，来寻找的最优分裂属性跟值，然后依次这样建树。保存规则，对于测试的时候就很方便了，直接把测试数据进行分片，进入map，map的输出就是<行号，预测的标签>，就是结果，就不需要reduce阶段。

        可以看到上面的那种思路会进行很多次的map-reduce任务，这无形中会造成很大的I/O压力，下面第二种思路是Google开发的Planet并行决策树集成系统，构建的是二叉树，下图是训练过程框架

 

       

       该过程分4个部分：1) 主机节点负责维护InMemory树节点列队、FindBestSplit 树节点列队、模型规则存储；2) 初始化过程负责确定树节点分裂需要从哪些属性选最优的，不过里面有一个trick，就是当属性值特别是数值型的，如果量少的话，就可以每一个值作为候选的分裂值，但是如果量非常多的话，一个一个选会很影响性能，一个替代的方法就是把那些值分桶(也就是相当于离散化了，但是还是数值型的)；3) InMemoryBuild 就是说如果到当前节点的时候，数据量比较小，能够在内存里面搞就直接在内存里面搞了；4) FindBestSplit 是说 如果到当前节点的时候，数据量非常大就需要分布式搞，具体的map-reduce过程跟上面第一种策略有点相似 ；原 Planet系统还支持并行的bagging跟boosting，但是sample的时候只能支持无放回的采样(不知道最近有没有更新)，功能也是非常强大

       总结：Mahout里面有随机森林的的分布式建树，它的策略是通过每个mapper来建一颗树，partition的数据也是原有的1/10（默认条件），这个值越大，单棵树的精度也越高，但是实际操作过程中，也并非样本越多，精度越高，况且forest的精度不仅跟单个分类器的精度有关，也跟分类器之间的多样性有关。其他的如梯度的boosting之前2009年的时候，雅虎算法研究院发过一篇该算法并行的文章。

 

K均值的 map-reduce   

       常用的聚类 算法，挖掘用户的群组相似性，常用的用户分层模型、细分模型都会用到相应的聚类的算法，该算法单机伪代码如下

 

输入：聚类数K，K个随机的聚类中心，训练集

输出：K个聚类中心，每个样本所属的组别

for i in I（迭代停止条件，通常用户可以自己设定或者让算法自己收敛即每个样本到各自中心的距离之和最短）

    for j in K:

        计算每个样本到每个聚类中心的距离

    距离最短的，就把该样本赋到该类别上

    根据新生成的K个组样本，更新K个聚类中心

end for

 

       从 算法的执行过程可以看出，跟KNN算法一样，非常适合并行处理，对于算法的每一次迭代可以分一下三个步骤

map端：输入<key,value>key是样本的行号，value就是样本的信息了，输出<key,value> key是该样本所属的中心点index， value就是样本的信息了

具体操作：1) 从输入的value里面解析特征属性值 

                  2) for i in K

                           计算到i个中心的距离

                      key=最近的那个中心的index，value 就是样本信息

Combine端：对Map的输出属于同一聚类的点做一个简单的累加，输入是map端的输出，输出是<kay,value>

是该样本所属的中心点index， value就是该类下的累加和跟总个数

Reduce端：任务是把Combine端的输出进行归总，更新聚类中心，输出就是<聚类中心代号，聚类中心>

 

       总结： K均值的并行处理也有成熟的开源工具(Mahout，spark-mllib，GPUlib)，该算法的结果不稳定，跟初始化中心有关系，对于这个问题的也有一些改进的算法如K中心算法，另外自动聚类(算法自动完成应该聚成几类)也是学术界研究的热点

 

先写到这里了，一篇文章太长了，自己看的累，呵呵

下篇预告

1）logisitc regression（有损跟无损的并行）

2）SVM/NN的map-reduce

3）关联挖掘(apriori，FP-growth)的并行策略

4）推荐系统的一些算法并行

 

参考资料：1）Map-Reduce for Machine Learning on Multicore NG的一篇nips文章；2 ）Mining   of   Massive  Datasets；3) http://www.cnblogs.com/vivounicorn/archive/2011/10/08/2201986.html