Triangle - Delaunay Triangulator

Triangle - Delaunay Triangulator 

[email protected]

Abstract. Triangle is a 2D quality mesh generator and Delaunay triangulator. Triangle was created as part of the Quake project in the school of Computer Science at Carnegie Mellon University by Jonathan R. Shewchuk. Triangle is a small C program and its Delaunay refinement algorithm for quality mesh generation is a hybrid one. It includes divide-and-conquer and incremental insertion algorithms and sweepline Delaunay triangulation algorithm. This paper is focused on the usage of the Triangle and visualization the triangulation result in OpenSceneGraph. 

Key words. Triangle, Delaunay Triangulator, Mesh Generator

1. Introduction

Triangle可以生成精确的Delaunay三角剖分，限定Delaunay三角剖分（Constrained Delaunay Triangulation），Conforming Delaunay Triangulation，Voronoi图（Voronoi Diagrams）和高质量的三角网格，即生成的网格中没有瘦长的三角形，所以适用于有限元分析（Finite Element Analysis）。 

在OpenCascade6.2.0版本之前，OpenCascade中网格的生成就是使用了这个开源库，由此可见Delaunay三角剖分算法和网格生成算法的重要性及广泛应用。 

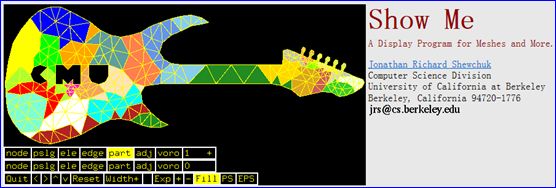
Figure 1.1 Triangle - A 2D Quality Mesh Generator and Delaunay Triangulator 

下载Triangle的源程序及更多与Triangle相关信息的网址如下所示： 

http://www.cs.cmu.edu/~quake/triangle.html

下载到源程序后，如果是Windows操作系统，还需要在triangle.h之前做些配置，如定义以下几个宏：

#define REAL double

#define ANSI_DECLARATORS

#include "triangle.h"

#undef REAL

在triangle.c中定义宏：#define NO_TIMER。有了上面的宏定义，可以编译出一个triangle.exe程序了。如果要将triangle用在自己的程序中，还需要定义#define TRILIBRARY。更多宏定义可以参考源程序。 

2. Triangle Usage

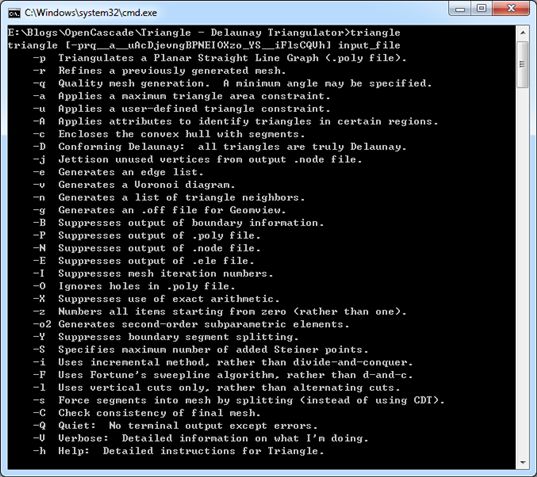
Triangle有很多开关，可以选择三角剖分和生成网格的方式，如下图所示： 

Figure 2.1 Options for the Triangle 

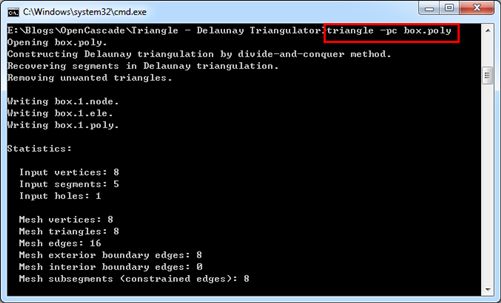
如对示例文件box.poly进行三角剖分，使用命令及生成结果统计信息如下所示： 

Figure 2.2 Triangle Usage 

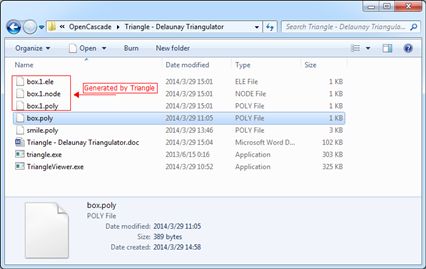
出现统计信息的同时也生成了一些文件，如顶点文件box.1.node和三角形文件box.1.ele，如下图所示： 

Figure 2.3 Nodes and Triangles data generated by Triangle 

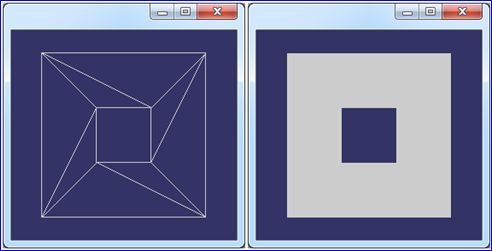
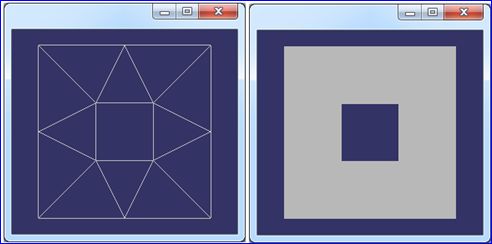
Figure 2.4 Triangulation Mesh Generated by Triangle[-pc] 

Figure 2.5 Triangulation Mesh Generated by Triangle[-pqc]

3. Displaying Meshes

在下载的程序中有用于显示网格的示例程序showme.c，不过只能用于Unix操作系统，不能用于Windows。 

Figure 3.1 Displaying the Meshes by ShowMe 

为了在Windows操作系统中看到生成的网格，用OpenSceneGraph编写了一个小程序TriangleViewer显示网格。其中读取node和element文件中数据的主要程序片段如下所示： 

std::string TriangleMesh::ReadLine(std::ifstream &theFile)

{

    std::string theBuffer;



    bool IsReadNextLine = false;



    do 

    {

        getline(theFile, theBuffer);



        // skip comment here.

        if ('#' == theBuffer[0])

        {

            IsReadNextLine = true;

        }

        else

        {

            IsReadNextLine = false;

        }

    }

    while (IsReadNextLine);



    return theBuffer;

}



void TriangleMesh::BuildMesh(const std::string& aPolyFile)

{

    std::stringstream ss;



    std::string theNodeFileName(aPolyFile + ".node");

    std::string theElementFileName(aPolyFile + ".ele");



    std::ifstream theNodeFile(theNodeFileName.c_str());

    std::ifstream theElementFile(theElementFileName.c_str());



    Standard_Integer theIndex = 0;

    Standard_Integer theNodeCount = 0;

    Standard_Integer theTriangleCount = 0;



    Standard_Integer theIndex1 = 0;

    Standard_Integer theIndex2 = 0;

    Standard_Integer theIndex3 = 0;



    Standard_Real x = 0.0;

    Standard_Real y = 0.0;



    // Read mesh size.

    ss << ReadLine(theNodeFile);

    ss >> theNodeCount;



    ss.str("");

    ss.clear();



    ss << ReadLine(theElementFile);

    ss >> theTriangleCount;



    mMesh = new Poly_Triangulation(theNodeCount, theTriangleCount, Standard_True);



    // Read nodes information.

    TColgp_Array1OfPnt2d& theNodes2d = mMesh->ChangeUVNodes();



    for (Standard_Integer n = 1; n <= theNodeCount; ++n)

    {

        ss.str("");

        ss.clear();



        ss << ReadLine(theNodeFile);

        ss >> theIndex >> x >> y;



        theNodes2d.SetValue(theIndex, gp_Pnt2d(x, y));

    }



    // Read triangles information.

    Poly_Array1OfTriangle& theTriangles = mMesh->ChangeTriangles();



    for (Standard_Integer t = 1; t <= theTriangleCount; ++t)

    {

        ss.str("");

        ss.clear();



        ss << ReadLine(theElementFile);

        ss >> theIndex >> theIndex1 >> theIndex2 >> theIndex3;



        theTriangles.SetValue(theIndex, Poly_Triangle(theIndex1, theIndex2, theIndex3));

    }

}

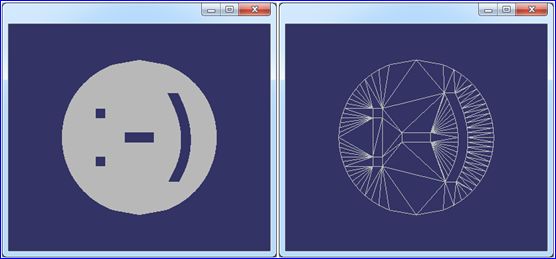
如下图所示为显示一个用不同命令生成的Smiley Face的网格： 

Figure 3.2 Generate Smiley Face Mesh by Triangle [-pc] 

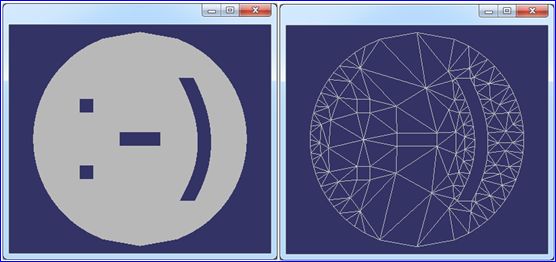
Figure 3.3 Generate Smiley Face Mesh by Triangle [-pqc] 

从上面两幅图中的网格可知，下面图中的网格质量较高，为去掉了瘦长的三角形而增加了一些顶点。 

4. Conclusions

在给Triangle程序输入数据时，顶点Vertex数据很好理解，只是一些二维点，但是如果加上开孔Hole后有些问题。后来才知道，需要在Poly文件中的Segments部分输入与孔相关线段形成的闭合区域，在孔Hole部分只需要输入位于孔中的任意一个点即可。 

将Triangle生成的结果可视化，可以看到Triangle生成的网格，方便看到Triangle的不同选项生成的网格效果。 

在OpenCascade6.2.0版本中，就以此二维Delaunay三角剖分工具为基础，实现了任意三维曲面的三角剖分，进而对其可视化。所以学习Triangle的用法，结合OpenCascade的源程序便于理解任意曲面的可视化实现的方法。 

对Delaunay三角剖分算法感兴趣的读者，可以参考相关书籍[3],[4],[5],[6]。 

5. References

1. Jonathan R. Shewchuk. Triangle: http://www.cs.cmu.edu/~quake/triangle.html

2. Jonathan R. Shewchuk, Triangle: Engineering a 2D Quality Mesh Generator and Delaunay Triangualtor, Springer-Verlag, Berlin, 1996 

3. 汪嘉业 王文平 屠长河 杨承磊. 计算几何及应用.  科学出版社. 2011 

4. 王成恩. 面向科学计算的网格划分与可视化技术. 科学出版社. 2011 

5. 周培德. 计算几何－算法设计与分析. 清华大学出版社. 2008 

6. Berg M D著 邓俊辉译. 计算几何－算法与应用. 清华大学出版社. 2009 

 

PDF Version: Triangle-Delaunay Triangulator