使用倍增算法(Prefix Doubling)构造后缀数组
如果采用对每个后缀排序的方法来生成后缀数组，即使采用快速排序，由于每次比较的对象是字符串（设输入字符串的长度为n），因此每一个比较操作的复杂度不再是常数，而是O(n)，快速排序本身的平均情况下时间复杂度为O(nlgn)，因此总的时间复杂度是O(n^2*lgn)，如果考虑到采用快速排序最坏情况下复杂度为O(n^2)，那么最坏时总的复杂度为O(n^3)，显然在输入串长度很大时这种做法不可取。
Prefix Doubling算法（倍增法）是构造后缀数组一个比较实用的算法。其基本思想是先计算出每个后缀的k-前缀的rank值，然后在此基础上计算每个后缀的2k-前缀rank值，k从1开始。直到每个后缀都排出先后顺序为止（任何两个后缀都不会相等，换句话说，每个后缀终究都能排出先后顺序）。在处理2k-前缀时，只需要使用基数排序（radix sort）算法，先后对两位数字排序（可以采用计数排序算法(counting sort)对每一位数字排序）。在最坏情况下，需要做lgn次基数排序，每一次基数排序的操作次数为2*O(n)，因此它的时间复杂度是O(nlgn)。倍增法虽然没有达到像DC3算法的线性复杂度，但是它的优点是实现比较简单，因此在实践中常被采用。
在以下实现中，当k=1时，由于只需要对输入串的每个字符排序，因此在采用基数排序时，只有一位数字需要排序。当k>1时，需要对两位数字排序（为考虑通用性，代码中Tuple.digits数组长度可以取>=1的任何整数，而不限于两位数字的基数排序）。如果rank数组中某个后缀具有最大rank值，而且该rank值等于输入串的长度，这时说明每一个后缀都排出了次序，因而可以提前终止程序。另外，假设字母表中最大的字符为MAX_CHAR。
注：rank数组中的rank值对应SA数组的下标+1。例如T=mississippi#,那么SA=(11,10,7,4,1,0,9,8,6,3,5,2),这里第7个后缀（即ippi$）在SA数组中的下标是2，因此Rank[7]=3。
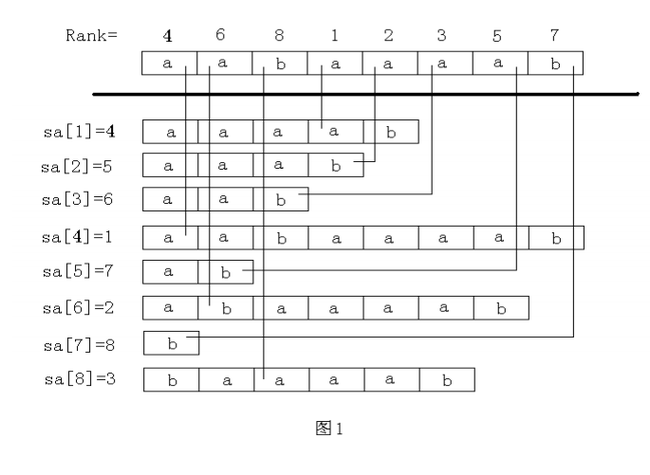
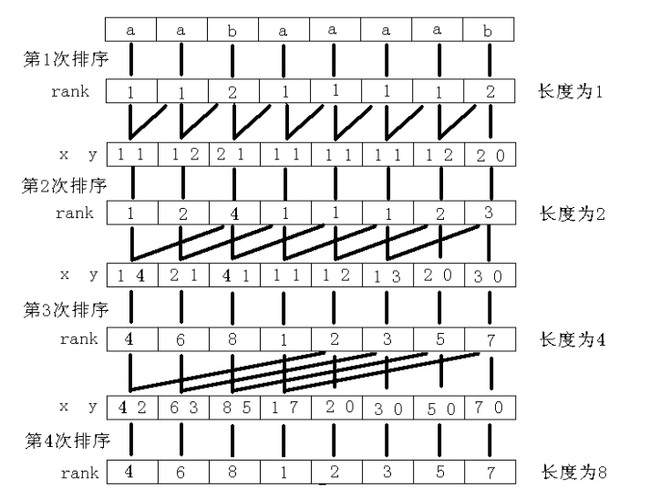
Prefix Doubling算法（倍增法）是构造后缀数组一个比较实用的算法。其基本思想是先计算出每个后缀的k-前缀的rank值，然后在此基础上计算每个后缀的2k-前缀rank值，k从1开始。直到每个后缀都排出先后顺序为止（任何两个后缀都不会相等，换句话说，每个后缀终究都能排出先后顺序）。在处理2k-前缀时，只需要使用基数排序（radix sort）算法，先后对两位数字排序（可以采用计数排序算法(counting sort)对每一位数字排序）。在最坏情况下，需要做lgn次基数排序，每一次基数排序的操作次数为2*O(n)，因此它的时间复杂度是O(nlgn)。倍增法虽然没有达到像DC3算法的线性复杂度，但是它的优点是实现比较简单，因此在实践中常被采用。
在以下实现中，当k=1时，由于只需要对输入串的每个字符排序，因此在采用基数排序时，只有一位数字需要排序。当k>1时，需要对两位数字排序（为考虑通用性，代码中Tuple.digits数组长度可以取>=1的任何整数，而不限于两位数字的基数排序）。如果rank数组中某个后缀具有最大rank值，而且该rank值等于输入串的长度，这时说明每一个后缀都排出了次序，因而可以提前终止程序。另外，假设字母表中最大的字符为MAX_CHAR。
注：rank数组中的rank值对应SA数组的下标+1。例如T=mississippi#,那么SA=(11,10,7,4,1,0,9,8,6,3,5,2),这里第7个后缀（即ippi$）在SA数组中的下标是2，因此Rank[7]=3。
实现：
/**
*
* Build Suffix Array using Prefix Doubling Algorithm
* see also: Udi Manber and Gene Myers' seminal paper(1991): "Suffix arrays: A new method for on-line string searches"
*
* Copyright (c) 2011 ljs (http://blog.csdn.net/ljsspace/)
* Licensed under GPL (http://www.opensource.org/licenses/gpl-license.php)
*
* @author ljs
* 2011-07-17
*
*/
public class PrefixDoubling {
public static final char MAX_CHAR = '\u00FF';
class Suffix{
int[] sa;
//Note: the p-th suffix in sa: SA[rank[p]-1]];
//p is the index of the array "rank", start with 0;
//a text S's p-th suffix is S[p..n], n=S.length-1.
int[] rank;
boolean done;
}
//a prefix of suffix[isuffix] represented with digits
class Tuple{
int isuffix; //the p-th suffix
int[] digits;
public Tuple(int suffix,int[] digits){
this.isuffix = suffix;
this.digits = digits;
}
public String toString(){
StringBuffer sb = new StringBuffer();
sb.append(isuffix);
sb.append("(");
for(int i=0;i<digits.length;i++){
sb.append(digits[i]);
if(i<digits.length-1)
sb.append("-");
}
sb.append(")");
return sb.toString();
}
}
//the plain counting sort algorithm for comparison
//A: input array
//B: output array (sorted)
//max: A value's range is 0...max
public void countingSort(int[] A,int[] B,int max){
//init the counter array
int[] C = new int[max+1];
for(int i=0;i<=max;i++){
C[i] = 0;
}
//stat the count in A
for(int j=0;j<A.length;j++){
C[A[j]]++;
}
//process the counter array C
for(int i=1;i<=max;i++){
C[i]+=C[i-1];
}
//distribute the values in A to array B
for(int j=A.length-1;j>=0;j--){
//C[A[j]] <= A.length
B[--C[A[j]]]=A[j];
}
}
//d: the digit to do countingsort
//max: A value's range is 0...max
private void countingSort(int d,Tuple[] tA,Tuple[] tB,int max){
//init the counter array
int[] C = new int[max+1];
for(int i=0;i<=max;i++){
C[i] = 0;
}
//stat the count
for(int j=0;j<tA.length;j++){
C[tA[j].digits[d]]++;
}
//process the counter array C
for(int i=1;i<=max;i++){
C[i]+=C[i-1];
}
//distribute the values
for(int j=tA.length-1;j>=0;j--){
//C[A[j]] <= A.length
tB[--C[tA[j].digits[d]]]=tA[j];
}
}
//tA: input
//tB: output for rank caculation
private void radixSort(Tuple[] tA,Tuple[] tB,int max,int digitsLen){
int len = tA.length;
int digitsTotalLen = tA[0].digits.length;
for(int d=digitsTotalLen-1,j=0;j<digitsLen;d--,j++){
this.countingSort(d, tA, tB, max);
//assign tB to tA
if(j<digitsLen-1){
for(int i=0;i<len;i++){
tA[i] = tB[i];
}
}
}
}
//max is the maximum value in any digit of TA.digits[], used for counting sort
//tA: input
//tB: the place holder, reused between iterations
private Suffix rank(Tuple[] tA,Tuple[] tB,int max,int digitsLen){
int len = tA.length;
radixSort(tA,tB,max,digitsLen);
int digitsTotalLen = tA[0].digits.length;
//caculate rank and sa
int[] sa = new int[len];
sa[0] = tB[0].isuffix;
int[] rank = new int[len];
int r = 1; //rank starts with 1
rank[tB[0].isuffix] = r;
for(int i=1;i<len;i++){
sa[i] = tB[i].isuffix;
boolean equalLast = true;
for(int j=digitsTotalLen-digitsLen;j<digitsTotalLen;j++){
if(tB[i].digits[j]!=tB[i-1].digits[j]){
equalLast = false;
break;
}
}
if(!equalLast){
r++;
}
rank[tB[i].isuffix] = r;
}
Suffix suffix = new Suffix();
suffix.rank= rank;
suffix.sa = sa;
//judge if we are done
if(r==len){
suffix.done = true;
}else{
suffix.done = false;
}
return suffix;
}
//Precondition: the last char in text must be less than other chars.
public Suffix solve(String text){
if(text == null)return null;
int len = text.length();
if(len == 0) return null;
int k=1;
char base = text.charAt(len-1); //the smallest char
Tuple[] tA = new Tuple[len];
Tuple[] tB = new Tuple[len]; //placeholder
for(int i=0;i<len;i++){
tA[i] = new Tuple(i,new int[]{0,text.charAt(i)-base});
}
Suffix suffix = rank(tA,tB,MAX_CHAR-base,1);
while(!suffix.done){ //no need to decide if: k<=len
k<<=1;
int offset = k>>1;
for(int i=0,j=i+offset;i<len;i++,j++){
tA[i].isuffix = i;
tA[i].digits=new int[]{suffix.rank[i],
(j<len)?suffix.rank[i+offset]:0};
}
int max = suffix.rank[suffix.sa[len-1]];
suffix = rank(tA,tB,max,2);
}
return suffix;
}
public void report(Suffix suffix){
int[] sa = suffix.sa;
int[] rank = suffix.rank;
int len = sa.length;
System.out.println("suffix array:");
for(int i=0;i<len;i++){
System.out.format(" %s", sa[i]);
}
System.out.println();
System.out.println("rank array:");
for(int i=0;i<len;i++){
System.out.format(" %s", rank[i]);
}
System.out.println();
}
public static void main(String[] args){
/*
//plain counting sort test:
int[] A= {2,5,3,0,2,3,0,3};
PrefixDoubling pd = new PrefixDoubling();
int[] B = new int[A.length];
pd.countingSort(A,B,5);
for(int i=0;i<B.length;i++)
System.out.format(" %d", B[i]);
System.out.println();
*/
String text = "GACCCACCACC#";
PrefixDoubling pd = new PrefixDoubling();
Suffix suffix = pd.solve(text);
System.out.format("Text: %s%n",text);
pd.report(suffix);
System.out.println("********************************");
text = "mississippi#";
pd = new PrefixDoubling();
suffix = pd.solve(text);
System.out.format("Text: %s%n",text);
pd.report(suffix);
System.out.println("********************************");
text = "abcdefghijklmmnopqrstuvwxyz#";
pd = new PrefixDoubling();
suffix = pd.solve(text);
System.out.format("Text: %s%n",text);
pd.report(suffix);
System.out.println("********************************");
text = "yabbadabbado#";
pd = new PrefixDoubling();
suffix = pd.solve(text);
System.out.format("Text: %s%n",text);
pd.report(suffix);
System.out.println("********************************");
text = "DFDLKJLJldfasdlfjasdfkldjasfldafjdajfdsfjalkdsfaewefsdafdsfa#";
pd = new PrefixDoubling();
suffix = pd.solve(text);
System.out.format("Text: %s%n",text);
pd.report(suffix);
}
}
测试：
Text: GACCCACCACC#
suffix array:
11 8 5 1 10 7 4 9 6 3 2 0
rank array:
12 4 11 10 7 3 9 6 2 8 5 1
********************************
Text: mississippi#
suffix array:
11 10 7 4 1 0 9 8 6 3 5 2
rank array:
6 5 12 10 4 11 9 3 8 7 2 1
********************************
Text: abcdefghijklmmnopqrstuvwxyz#
suffix array:
27 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
rank array:
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 1
********************************
Text: yabbadabbado#
suffix array:
12 1 6 4 9 3 8 2 7 5 10 11 0
rank array:
13 2 8 6 4 10 3 9 7 5 11 12 1
********************************
Text: DFDLKJLJldfasdlfjasdfkldjasfldafjdajfdsfjalkdsfaewefsdafdsfa#
suffix array:
60 0 2 1 5 7 4 6 3 59 47 54 30 34 41 17 11 25 53 29 33 9 19 23 13 56 44 37 50 48 58 46 10 55 36 39 15 31 20 27 51 40 16 24 32 35 43 21 28 8 22 14 42 52 18 12 57 45 38 26 49
rank array:
2 4 3 9 7 5 8 6 50 22 33 17 56 25 52 37 43 16 55 23 39 48 51 24 44 18 60 40 49 20 13 38 45 21 14 46 35 28 59 36 42 15 53 47 27 58 32 11 30 61 29 41 54 19 12 34 26 57 31 10 1