POJ 1185 炮兵阵地(动态规划+状态压缩)
炮兵阵地
Description
司令部的将军们打算在N*M的网格地图上部署他们的炮兵部队。一个N*M的地图由N行M列组成,地图的每一格可能是山地(用"H" 表示),也可能是平原(用"P"表示),如下图。在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队);一支炮兵部队在地图上的攻击范围如图中黑色区域所示:
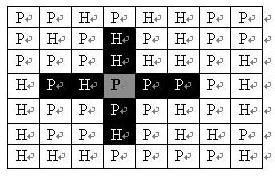
如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。
现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。

如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。
现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。
Input
第一行包含两个由空格分割开的正整数,分别表示N和M;
接下来的N行,每一行含有连续的M个字符('P'或者'H'),中间没有空格。按顺序表示地图中每一行的数据。N <= 100;M <= 10。
接下来的N行,每一行含有连续的M个字符('P'或者'H'),中间没有空格。按顺序表示地图中每一行的数据。N <= 100;M <= 10。
Output
仅一行,包含一个整数K,表示最多能摆放的炮兵部队的数量。
Sample Input
5 4 PHPP PPHH PPPP PHPP PHHP
Sample Output
6
分析:思路很简单,因为每个位置要么放一门炮、要么不放,每行最多只有10个位置,所以可以用位存储状态,大体分如下两步:
1.计算出每行所有的合法状态,并用位表示。
2.DP~~~
f[p][i][j] = Max{f[p-1][j][k]+ct(p,i)} f[p][i][j]表示第p行取第i种方案,p-1行取第j种方案时的最大值,ct(p,i)表示第p行用第i种方案时用的炮的个数。
求整数x用二进制表示时1的个数,只需要让x不断的执行x &= (x-1)就可以了,执行了多少次就有多少个1。
为什么呢??可以分两种情况,如果x最后一位是1,那么执行一次与运算可以把这个1消掉,但是如果最后一位是0呢??这个时候消掉的是最靠右的一个1,呵呵,可以简单的画一下看看。总之就是逐步消掉最后一个1,消了几次就有几个1啦~~
第一个代码如下:
1 # include<iostream> 2 # include<cstdio> 3 # include<cstring> 4 using namespace std; 5 6 const int N = 101; 7 const int M = 11; 8 const int INF = 0xffffff; 9 10 int n,m; 11 int ct[N][65]; //ct[i][0]表示第i行放置炮的方案数,ct[i][j],j>0 表示第j种方案的状态 12 int tt[1030]; //tt[i]表示 i 表示成2进制时的1的个数,即放置炮的数目 13 int f[N][65][65]; //f[p][i][j]表示第p行取第i种方案,p-1行取第j种方案时的最大值 14 int hash[1030][1030]; 15 char map[N][M]; 16 17 int max(int x,int y){ 18 return x>y ?x : y; 19 } 20 21 //这一行的状态 22 void Init_row(const int &r,int x,int key){ //r是第几行,x表示2进制的位数,key表示状态 23 if(x==m){ 24 ct[r][0] ++; //ct[r][0]表示这一行状态的数目 25 ct[r][ct[r][0]] = key; //ct[r][i]表示第r行第i个状态 被压缩后的数字 26 return ; 27 } 28 if(map[r][x] == 'P' && (key & 1)==0 &&(key & 2)==0) //可以表示成状态 29 Init_row(r,x+1,(key<<1)+1); 30 Init_row(r,x+1,key<<1); 31 } 32 33 bool Yes(int x,int y){ //判断map[x][y]能不能放置炮,会不会进入其他人射程 34 int xx=x,yy=y; 35 if(hash[x][y] != -1) return hash[x][y]; 36 while(x||y){ 37 if((x&1)==1 && (y&1)==1){ 38 hash[xx][yy] = false; 39 break; 40 } 41 x>>=1; 42 y>>=1; 43 } 44 if(hash[xx][yy] == -1) hash[xx][yy] = 1; 45 hash[yy][xx] = hash[xx][yy]; 46 return hash[xx][yy]; 47 } 48 49 void Dp(){ 50 int i,j,k,p,u,v,w; 51 for(i=1;i<=ct[1][0];i++) f[1][i][0] = tt[ct[1][i]]; //第1行放置炮的数目 52 if(n>=2) //第2行放置炮的数目 53 for(i=1;i<=ct[2][0];i++){ 54 u=ct[2][i]; 55 for(j=1;j<=ct[1][0];j++){ 56 f[2][i][j] = -INF; 57 v = ct[1][j]; 58 if(Yes(u,v)) 59 f[2][i][j] = max(f[2][i][j],f[1][j][0]+tt[u]); 60 } 61 } 62 63 for(p=3;p<=n;p++){ 64 for(k=1;k<=ct[p][0];k++){ 65 w=ct[p][k]; 66 for(i=1;i<=ct[p-1][0];i++){ 67 v=ct[p-1][i]; 68 f[p][k][i] = -INF; 69 if(!Yes(v,w)) continue; 70 for(j=1;j<=ct[p-2][0];j++){ 71 u=ct[p-2][j]; 72 if(Yes(u,v) && Yes(u,w)) 73 f[p][k][i] = max(f[p][k][i],f[p-1][i][j] + tt[w]); 74 } 75 } 76 } 77 } 78 } 79 80 int main(){ 81 int i,j,temp,ans; 82 memset(hash,-1,sizeof(hash)); 83 for(i=0;i<1030;i++){ 84 temp = i; 85 tt[i] = 0; 86 while(temp){ //整数temp表示成2进制时1的个数 87 tt[i]++; 88 temp &= (temp -1); 89 } 90 } 91 scanf("%d%d",&n,&m); 92 for(i=1;i<=n;i++) 93 scanf("%s",map[i]); 94 for(i=1;i<=n;i++){ 95 ct[i][0] = 0; 96 Init_row(i,0,0); 97 } 98 Dp(); 99 ans = -INF; 100 if(n==1) 101 for(i=1;i<=ct[n][0];i++) 102 ans = max(ans,f[n][i][0]); 103 else{ 104 for(i=1;i<=ct[n][0];i++) 105 for(j=1;j<=ct[n-1][0];j++) 106 ans = max(ans,f[n][i][j]); 107 } 108 printf("%d\n",ans); 109 return 0; 110 }
由于M很小,最多为10,所以可以对行进行状态压缩。二进制对应位为1表示放炮兵,为0表示空。我们可以事先生成所有有效的状态,即二进制数任何两个1都要相差两位以上,同时用数组记下此状态有多少个炮兵。对于地形也进行状态压缩,用1表求高地,0表示平原。判断某个状态能否放到某个地形,就是地形状态为1的地方,放置炮兵状态一定为0,这点可以用位运算解决。判断两个状态能否放在相邻行与此相同。
代码如下:
1 # include <iostream> 2 using namespace std; 3 4 const int G = 70; 5 const int N =101; 6 const int M =11; 7 8 int d[2][G][G];//滚动数组 9 int ph[N],f[G];//ph数组用于判断状态在第i行是否满足在P的平原设置,f数组则存放满足的状态 10 int n,m,g;//g为所有状态数 11 12 int OneC(int x){//计算x二进制1的个数,这个算法很优秀,是在《编程之美》书中学到的。 13 int t =0; 14 while(x){ 15 t ++; 16 x &= (x-1); 17 } 18 return t; 19 } 20 void DP(){//dp 21 for(int k =2; k < n ;k++){ 22 for(int i =0; i< g; i++){ 23 if(ph[k] != (ph[k] | f[i]))continue;//判断状态f[i]是否满足在平原设置炮台 24 for(int j = 0;j < g; j++){ 25 if(ph[k-1] != (ph[k-1] | f[j]))continue; 26 if(f[i] & f[j])continue;//判断第k行和第k-1行的炮台是否有彼此击中 27 for(int q=0; q< g; q ++){ 28 if(ph[k-2] != (ph[k-2] | f[q]))continue; 29 if(f[q] & f[j])continue; 30 if(f[i] & f[q])continue; 31 d[k%2][i][j] = max(d[k%2][i][j], d[(k+1)%2][j][q] + OneC(f[i])); //状态方程 32 } 33 } 34 } 35 } 36 } 37 int main(){ 38 scanf("%d %d",&n,&m); 39 int i ,j; 40 char ch[M]; 41 for(i =0;i < n; i++){//计算ph[] 42 ph[i] =0; 43 scanf("%s", ch); 44 for(j =0; j < m; j++){ 45 if(ch[j] == 'P') 46 ph[i] += (1<<(m-j-1)); 47 } 48 } 49 int v = 1<<m; 50 for(i =0,g =0; i< v;i++){//挑选合法状态 51 if(((i & (i << 2)) == 0) && (i & (i <<1))==0)//这个想法不错哦。 52 f[g++] = i; 53 } 54 int pMax ; 55 if(n ==1){ 56 pMax = 0; 57 for(i =0; i<g ; i++){ 58 if((ph[0] | f[i])==ph[0]) 59 pMax = max( pMax , OneC(f[i])); 60 } 61 printf("%d" ,pMax); 62 return 0; 63 } 64 memset(d, 0,sizeof(d)); 65 pMax = 0; 66 for(i =0; i < g; i++){//初始化d 67 if(ph[1] != (ph[1] | f[i]))continue; 68 for(j =0 ;j < g; j++){ 69 if(ph[0] != (ph[0] | f[j]))continue; 70 if((f[i] & f[j]) ==0){ 71 d[1][i][j] = OneC(f[i]) + OneC(f[j]); 72 pMax = max (pMax , d[1][i][j]); 73 } 74 } 75 } 76 if(n ==2){ 77 printf("%d" ,pMax); 78 return 0; 79 } 80 DP(); 81 for(i =0; i < g; i ++){ 82 for(j =0; j< g; j++){ 83 pMax = max( pMax ,d[(n+1)%2][i][j]); 84 } 85 } 86 printf("%d", pMax); 87 return 0; 88 }
代码如下:
1 # include<cstdio> 2 # include<string> 3 # include<cstring> 4 # include<iostream> 5 # include<cmath> 6 # include<algorithm> 7 using namespace std; 8 int n,m,sum,num,sta[1<<11],cot[1<<11],dp[105][105][105],a[105]; 9 bool fit(int x,int y) 10 { 11 if(x&y) 12 return 0; 13 return 1; 14 } 15 void init() 16 { 17 sum=1<<m;num=0; 18 for(int i=0;i<sum;i++) 19 { 20 if(i&(i<<1)||i&(i<<2)) 21 continue; 22 sta[num]=i; 23 int temp = i,count=0; 24 while(temp) 25 { 26 count++; 27 temp&=temp-1; 28 } 29 cot[num++]=count; 30 } 31 } 32 void DP() 33 { 34 int ans=0; 35 for(int i=0;i<num;i++) 36 { 37 if(!fit(a[1],sta[i])) 38 continue; 39 dp[1][0][i] = cot[i]; 40 if(ans<dp[1][0][i]) 41 ans=dp[1][0][i]; 42 } 43 for(int i=2;i<=n;i++) 44 for(int j=0;j<num;j++) 45 for(int k=0;k<num;k++) 46 { 47 if(!fit(sta[k],sta[j])||!fit(a[i],sta[k])||!fit(a[i-1],sta[j])) 48 continue; 49 for(int l=0;l<num;l++) 50 { 51 if(!fit(sta[k],sta[l])||!fit(sta[j],sta[l])||!fit(a[i-2],sta[l])||!dp[i-1][l][j]) 52 continue; 53 dp[i][j][k]=max(dp[i][j][k],dp[i-1][l][j]+cot[k]); 54 if(ans<dp[i][j][k]) 55 ans=dp[i][j][k]; 56 } 57 } 58 printf("%d\n",ans); 59 } 60 int main() 61 { 62 char s; 63 scanf("%d%d",&n,&m); 64 getchar(); 65 init(); 66 for(int i=1;i<=n;i++) 67 { 68 for(int j=1;j<=m;j++) 69 { 70 scanf("%c",&s); 71 if(s=='H') 72 { 73 int tem=1<<(j-1); 74 a[i]+=tem; 75 } 76 } 77 getchar(); 78 } 79 DP(); 80 return 0; 81 }
另附转的一篇http://www.cnblogs.com/acm-bingzi/p/3278901.html