等值线的追踪算法--曲线光滑(3)
唉,我以前常常都在说,人是不可以闲下来的,闲下来就容易出事,这不,我一时想停下来,就在寝室里看
了两天的电影,唉,我啦...........
这一次我要说的就是我前面想好要说的等值线的光滑,说到等值线的光滑,我就提一下大家,不知道大家还记不记得
在类库中有这样的两个函数,Graphics.DrawCurve 方法和Graphics.DrawBezier 方法,说到这两函数,那可能就
有人要说,光滑那还不简单,把点传进去不就好了,不错,这样也是一种方法,也达到了比较好的光滑有效果,我在
做这个光滑的时候,是先找到的我下面要讲的那种方法,后来才找到这两个函数,那时我可是大笑,可是笑过之后,
我还是不得不在这两种方法中做出选择,因为我们要选一个更加的适合我们项目的文法,于是也就有了我下面的这篇
文章,至于为什么,我下面在说。
等值线的光滑,可能有的比较的了解,她分为两类拟合曲线和逼近曲线,也就是过点型和不过点型,过点型有三次样条
和抛物线样条曲线,不过点的有B样条曲线,还有 Bezier曲线,当然还有好多,我也不是非常的了解,也象我前面说的,
只是做到了够我当前项目用的程度,要了解更深的就自己多查一下这方面的资料,还蛮多的,算法这个东西,
我也觉得有时候蛮讨厌的,常常都弄得人头疼,但做出来了又让人很高兴,我做项目最大的感受就是,一个项目比较难做的
就是构架和算法,而我在项目里面做的比较多的就是算法,弄得人头疼,当然我说的比较难做也只是说的是开发,至于一
个项目里面的什么销售呀什么的,我就没有什么了解了。
一种算法的形成都有都其存在的理由, 也并不是说这种就一定好,那种就一定不好,就象我用排序算法的时候就一直只用
插入排序一样,简单,速度也可以达到要求,我现在就说一种比较简单的过点型(拟合型)的光滑算法,抛物线样条算法,
为什么不用三次样条算法,因为三次样条算法有一个要求,就是每一个点都要有导数,这个可是一个比较苛刻的要求,大家
要知道,在光滑的时候如果是在B点这样的位置用三次样条算法就不好做了,也可能有人会说那我把X,Y轴对换不就好了吗?
那我问大家你把轴对换就一定好了吗,你不信,就多想想,当然也不是说不可以,如果你硬是要那样做的话,你就不得不时时
去担心,我的这个点这里要不要将X换成Y,不过我有更好的办法。
抛物线样条就是我要说的一类好的方法,这里我也要感谢clever101,因为这个方法就是他做出来的,我只不过是拿他的讲讲
而已,抛物线拟合说到底就是三个三个点的拟合,具体的原文大家可以看一下这个:
http://blog.csdn.net/clever101/archive/2006/06/03/771160.aspx
我也不多说了,但我还是将他copy到这里 :
========================================================
假如我们采用矢量表达式来表示参数化的二次曲线,那么可以把抛物线的表达式写成如下的一般形式:
P(t)=A1+ A2t+ A3t2 (0=<t<=1)
该抛物线过P1, P2, P3三个点,并且:
1. 抛物线以P1点为始点。当参变量t=0时,曲线过P1点;
2. 抛物线以P3点为终点。当参变量t=0时,曲线过P3点;
3. 当参变量t=0.5时,曲线过P2点,且切矢量等于P3—P1。
t=0: P(0)= A1= P1
t=1: P(1)= A1 + A2+ A3=P3
t=0.5:P(0.5)= A1 + 0.5A2+0.25 A3=P2
通过解联立方程,得到三个参数A1 、 A2、 A3分别为:
A1 = P1
A2=4 P2—P3—3P1
A3=2P1+2P3—4P2
把求出的这三个系数的值,代入抛物线的表达式P(t)=A1+ A2t+ A3t2
得:P(t)=(2t—3t+1)P1 +(4t—4t2)P2+(4t2—t)P3 (0=<t<=1)
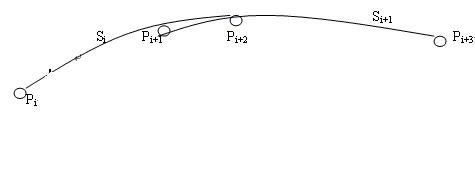
设有一离散型值点列Pi(i=1,2,……,n),每经过相邻三点作一段抛物线,由于有n个型值点,所以可以做n-2条抛物线段。
在这n—2条抛物线段中,第i条抛物线段为经过Pi, Pi+1, Pi+2三点,所以它的表达式应为:Si(ti)=(2t2i—3ti+1)Pi
+(4 ti—4 t2i) Pi+1 +(2t2i—ti) Pi+2 (0=< ti <=1)
同理,第i+1条抛物线段为经过Pi+1, Pi+2, Pi+3三点,所以它的表达式应为:Si+1(ti+1)=(2t2i+1—3ti+1+1)Pi+1
+(4 ti+1—4 t2i+1) Pi+2 +(2t2i+1—ti+1) Pi+3 (0=< ti+1 <=1)
一般来说,每两段曲线之间的搭接区间,两条抛物线是不可能重合的。如下图所示:
显然,对于拟合曲线来说,整个型值点必须只能用一条光滑的曲线连接起来。为了做到这一点,必须找一种方法把Si
和Si+1 这样的曲线段的共同区间结合起来。这种方法就是加权合成方法。
我们设共同区间的函数是Pi+1(t)=f (T ) Si(ti)+g ( T) Si+1(ti+1). 其中f (T ) 和 g ( T) 是权函数。在抛物样条
曲线中我们取简单的一次函数为权函数,且具有互补性,设
f (T ) =1—T
g ( T) =T
这样Pi+1(t)= (1—T ) Si(ti)+ T Si+1(ti+1).因为 函数中有T、ti和ti+1三个参数,因此接下来我们的工作是统一参数。
我们可以三个参变量统一形式为:
T=2t
ti=0.5+t
ti+1=t
这样
Pi+1(t)= (—2t3+4t2—t)Pi +(12t3—410t2+1) Pi+1 +(—12t3+8t2+t) Pi+2 +(4t3—2t2) Pi+3 (0=< ti <=0.5)
从几何意义上说,函数Pi+1(t)表示的上图的点Pi+1,到Pi+2 之间的线段。但是我们应该看到这种方法从n个点中只能得到
n—3段曲线。但是n个型值点应有n—1段曲线。一个直接的想法是添加两个辅助点。那么如何添加呢?
方法一:两个辅助点为P0和Pn+1, P0=P1,Pn+1= Pn ,这样画出的曲线为一条不闭合的自由曲线。
方法二:添加三个辅助点,P0、Pn+1和Pn+2,然后P0=Pn,Pn+1= P1, ,Pn+2= P2,这样画出的曲线为一条闭合的曲线。
=======================================================
这种方法比较好的解决了我的问题,这种方法一,它过点,过所有的观察点,二,也没有了什么X,Y轴对换的问题,三,相对简单,
不象别的程序算法都是一大堆一大堆的,现在我也没有发现它有什么问题,这也就回答了我为什么用这种方法了。顺便说一句,
这个也只是一个思路而已,大家要自己多想想,看有没有不适合自己的地方,自己修改吧,我开始的时候完完全全用的是他的
可是没有达到我的要求,我也是做了一些小改动的。
附图两张:
附上示例程序:以后我会将我做的一整套等值线都上传的,这里也感谢clever101。
http://files.cnblogs.com/ouzi/等值线/ParspTest.rar