上篇博文主要介绍的是数据结构的线性结构,我们这篇博文介绍非线性结构—树与二叉树,我先介绍树的一些基本概念,树的遍历,再介绍二叉树相关概念和特性,以及二叉树的遍历,最后再树与二叉树的对比,总结。
树为了描述现实世界的层次结构,树结构中一个数据元素可以有两个或两个以上的直接后继元素。
树的基本概念:
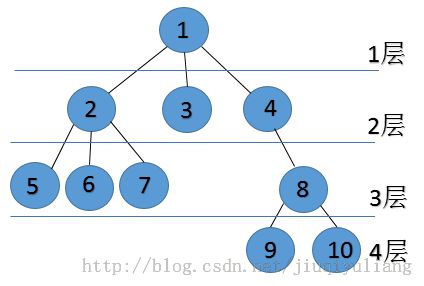
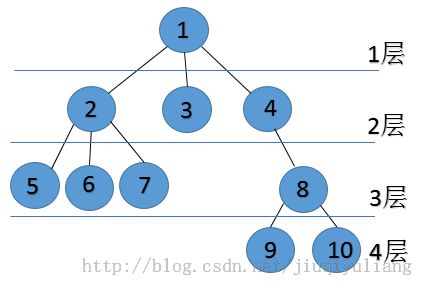
树的概念是学习树的关键所在,掌握了树的基本概念,学会树与二叉树,so easy。我通过一棵树来了解树的基本概念,如下图
1、结点的度
结点的度是子结点的个数。例如:结点1有三个字结点2,3,4,所以结点1的度为3。
2、树的度
树的度等于所有结点度中度最高的值。例如:上图中结点度最高为3,所以树的度为3。
3、叶子结点
叶子结点是度为0的结点即没有子结点的结点。例如:上图中3,5,6,7,9,10。
4、分支结点
分支结点是除了叶子结点,树中的其他所有结点。例如:上面树的分支结点为1,2,4,8。
5、内部结点
内部结点是除了根结点以及叶子结点或在分支结点的基础之上在去掉根结点。例如:上面树的内部结点为2,4,8。
6、父结点、子结点、兄弟结点
父节点、子结点和兄弟结点是相对而言的。例如:结点1是结点2,3,4的父节点,结点2,3,4也是结点1的子结点,结点2,3,4又是兄弟结点。
7、层次
图中我们已经表出来了,根为第一层,根的孩子为第二层,依此类推,若某结点在第i层,则其孩子结点在第i+1层。
树的遍历
树的遍历特别简单,我们还是以上面的树为例:
1、前序遍历
基本思想:前序遍历就是先访问根结点,再访问叶子结点。
图中树的前序遍历为:1,2,5,6,7,3,4,8,9,10。
2、后序遍历
基本思想:本后序遍历就是先访问子结点,再访问根结点。
图中树的后序遍历为:5,6,7,2,3,9,10,8,4,1。
3、层次遍历
基本思想:从第一层开始,依此遍历每层,直到结束。
图中树的层次遍历为:1,2,3,4,5,6,7,8,9,10。
二叉树的一些相关概念和特性
学习二叉树的特性几乎可以帮助我们解决所有的二叉树问题,在学习二叉树特性一定要通过上面给出的二叉树进行实践,实践出真理,同时,印象也会更深刻。
一般二叉树性质:
- 在非空二叉树的k层上,至多有2k个节点(k>=0)
- 高度为k的二叉树中,最多有2k+1-1个节点(k>=0)
- 对于任何一棵非空的二叉树,如果叶节点个数为n0,度数为2的节点个数为n2,则有: n0 = n2+ 1
完全二叉树性质:
- 具有n个节点的完全二叉树的高度k为[log2n]
- 对于具有n个节点的完全二叉树,如果按照从上(根节点)到下(叶节点)和从左到右的顺序对二叉树中的所有节点从0开始到n-1进行编号,则对于任意的下标为k的节点,有:
- 如果k=0,则它是根节点,它没有父节点;如果k>0,则它的父节点的下标为[(i-1)/2];
- 如果2k+1 <= n-1,则下标为k的节点的左子结点的下标为2k+1;否则,下标为k的节点没有左子结点.
- 如果2k+2 <= n-1,则下标为k的节点的右子节点的下标为2k+2;否则,下标为k的节点没有右子节点
满二叉树性质:
在满二叉树中,叶节点的个数比分支节点的个数多1
二叉树遍历
1、前序遍历(与树的前序遍历一样)
基本思想:先访问根结点,再先序遍历左子树,最后再先序遍历右子树即根—左—右。
图中前序遍历结果是:1,2,4,5,7,8,3,6。
2、中序遍历
基本思想:先中序遍历左子树,然后再访问根结点,最后再中序遍历右子树即左—根—右。
图中中序遍历结果是:4,2,7,8,5,1,3,6。
3、后序遍历
基本思想:先后序遍历左子树,然后再后序遍历右子树,最后再访问根结点即左—右—根。
图中后序遍历结果是:4,8,7,5,2,6,3,1。
4、层次遍历(与树的层次遍历一样)
基本思想:从第一层开始,依此遍历每层,直到结束。
图中层次遍历结果是:1,2,3,4,5,6,7,8。
树与二叉树区别
1、树可以有多个子结点,二叉树最多只能两个结点。
2、树中的子结点是无序的,二叉树是分左子结点和右子结点。
3、二叉树不是特殊树,而是独立的数据结构。
总结
这篇博文都是树的基本内容,这些基本内容可以帮助你更加深刻的理解树的其他内容,只要你能努力,世界充满爱。
后续博客的更新列表,敬请期待。
我的软考之路(一)——开篇(已更新)
我的软考之路(二)——J2SE宏观总结(已更新)
我的软考之路(三)——数据结构与算法(1)之线性表(已更新)
我的软考之路(四)——数据结构与算法(2)之树与二叉树(已更新)
我的软考之路(六)——数据结构与算法(4)之八大排序(已更新)