哈希表的概念
哈希表又称散列表,是一种线性的存储结构。是根据关键码值(Key Value)而直接进行访问的数据结构。它通过把关键码值映射到哈希表中的一个位置来访问记录,以加快查找的速度。这个映射函数就做散列函数,存放记录的数组叫做散列表。
哈希表存储思路
以数据中每个元素的关键字K为自变量,通过散列函数h(k)计算出函数值,以该函数值作为一块连续存储空间的的单元地址,将该元素存储到函数值对应的单元中。但是存在这样的问题,对于两个关键字K1和k2,可能k1!=k2,但是h(k1)==h(k2),此时就发生了冲突,这种叫做哈希冲突。
哈希函数的构造方法
构造哈希函数的目标是使得到的哈希地址尽可能均匀地分布在n个连续内存单元地址,同时使计算过程尽可能简单,以达到尽可能高的时间效率。根据关键字的结构和分布的不同,可构造出许多不同的哈希函数。
1.直接定址法
直接定址法是以关键字k本身或关键字加上某个数字常量c作为哈希地址的方法。哈希函数为
h(k)=k+c
这种哈希函数计算简单,并且不可能发生冲突。若关键字分布不连续将造成内存单元的大量浪费。
2.数字分析法
分 析一组数据,比如一组员工的出生年月,这时我们发现出生年月的前几位数字一般都相同,因此,出现冲突的概率就会很大,但是我们发现年月日的后几位表示月 份和具体日期的数字差别很大,如果利用后面的几位数字来构造散列地址,则冲突的几率则会明显降低.因此数字分析法就是找出数字的规律,尽可能利用这些数据 来构造冲突几率较低的散列地址
3.除留余数法
除留余数法是用关键字k除以某个不大于哈希表长度m的数p所得的余数作为哈希地址方法,哈希函数为:
h(k)=k %p(取余)
其中,p<=m;
除留余数法是最经常使用的一种哈希函数。这种方法关键是选好p,研究表明,p应该选取不大于m的素数时效果最好
哈希表冲突处理
1.开放定址法
当 关键字key的哈希地址p=H(key)出现冲突时,以p为基础,产生另一个哈希地址p1,如果p1仍然冲突,再以p为基础,产生另一个哈希地址 p2,…,直到找出一个不冲突的哈希地址pi ,将相应元素存入其中。这种方法有一个通用的再散列函数形式:Hi=(H(key)+di)%m i=1,2,…,n,其中H(key)为哈希函数,m 为表长,di称为增量序列。增量序列的取值方式不同,相应的再散列方式也不同。主要有以下两种:
(1)线性探索法
线性探索法是从发生冲突的地址d开始,一次探索d的下一个地址(当到达表尾时,下一个地址就是表头),直到找到空闲单元为止。线性探索的数学表达式为:
d0=h(k);
di=(d0+i )% m(取向下一个地址单元)
线性探索容易产生堆积问题。
(2)平方探测法
设发生冲突的地址为d,则平方探测法的探测序列为d+1^2;d+2^2;d+3^2,......其数学表达式为:
d0=h(k);
di=(d0+i^2)%m
平方探测法是一种比较好的处理冲突方法,可以避免出现堆积问题。缺点是不能探索到哈希表上的所有单元。
下面使用除留余数法加线性探索法来建立查找哈希表
设哈希表长度为13,插入数据为:{16,74,60,43,54,90,46,31,29,88,77};
根据除留余数法应取不大于哈希表长度的素数,所有取p=13;
定义哈希表结构:
#define MAX 13//哈希表长度
#define p 13 //不大于哈希表长度的素数
#define NULLKEY -1 //空关键字
#define DELKEY -2 //删除关键字
//除留余数法加线性探索法建立哈希表
struct node
{
int key;//关键字
string data;//数据域
int num;//探测次数
//初始化探索次数为0,关键字为空关键字
node()
{
num=0;
key=NULLKEY;
}
};
建立哈希表的代码为:
//建立哈希表
void Create(node hash[])
{
int data[11]={16,74,60,43,54,90,46,31,29,88,77};//生成哈希表数据
for(int i=0;i<11;i++)
{
int count=0;
int temp=data[i];
//关键字插入
while(true)
{
if(hash[temp%p].key==NULLKEY||hash[temp%p].key==DELKEY)//没冲突
{
count++;
hash[temp%p].key=data[i];//关键字插入
hash[temp%p].num=count;//探索次数
break;
}
else
{
temp=(temp+1)%p;//线性探查法
count++;//探测次数加一
}
}
}
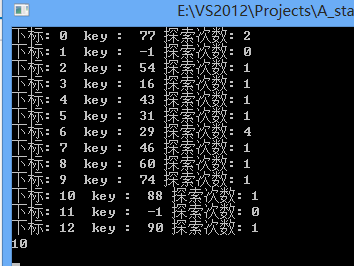
for(int i=0;i<13;i++)
cout<<"下标: "<<i<<" key : "<<hash[i].key<<" 探索次数: "<<hash[i].num<<endl;
}
哈希表查询
//哈希表查找
int Search(node hash[],int key)
{
int adr=key%p;
while(hash[adr].key!=NULLKEY&&hash[adr].key!=key)
{
adr=(adr+1)%p;
}
if(hash[adr].key==key) //查找成功返回地址
return adr;
else //查找失败
return -1;
}
调用main函数为:
int main()
{
node hash[MAX];//哈希表数组
Create(hash);
int result=Search(hash,88);
cout<<result<<endl;
return 0;
}
最后运行结果为:
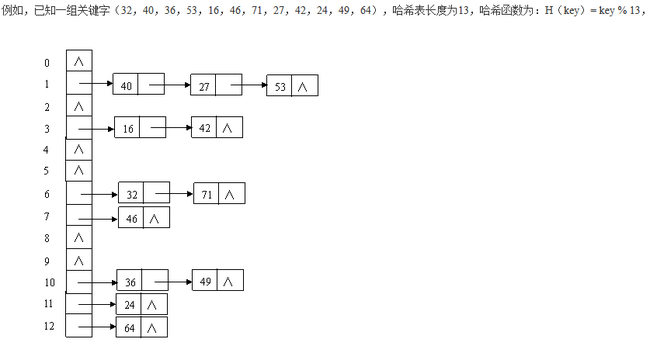
2.拉链法
拉链法是把所有同义词用链表连接起来的方法,这样,哈希表每个单元中存放的不再是记录本身,而是相应同义词单链表的头指针。拉链法需要额外的空间来存放指针
拉链法的优点与开放定址法相比,拉链法有如下几个优点:
(1)拉链法处理冲突简单,且无堆积现象,即非同义词决不会发生冲突,因此平均查找长度较短;
(2)由于拉链法中各链表上的结点空间是动态申请的,故它更适合于造表前无法确定表长的情况;
(3)开放定址法为减少冲突,要求装填因子α较小,故当结点规模较大时会浪费很多空间。而拉链法中可取 α≥1,且结点较大时,拉链法中增加的指针域可忽略不计,因此节省空间;
(4) 在用拉链法构造的散列表中,删除结点的操作易于实现。只要简单地删去链表上相应的结点即可。而对开放地址法构造的散列表,删除结点不能简单地 将被删结点的空间置为空,否则将截断在它之后填入散列表的同义词结点的查找路径。这是因为各种开放地址法中,空地址单元(即开放地址)都是查找失败的条 件。 因此在用开放地址法处理冲突的散列表上执行删除操作,只能在被删结点上做删除标记,而不能真正删除结点。
拉链法的缺点
拉链法的缺点是:指针需要额外的空间,故当结点规模较小时,开放定址法较为节省空间,而若将节省的指针空间用来扩大散列表的规模,可使装填因子变小,这又减少了开放定址法中的冲突,从而提高平均查找速度。
拉链法的实现使用链表实现,实现过程比较简单,这里就不再编写拉链法实现的代码了。