1. Digraph: Set of vertices connected pairwise by directed edges.
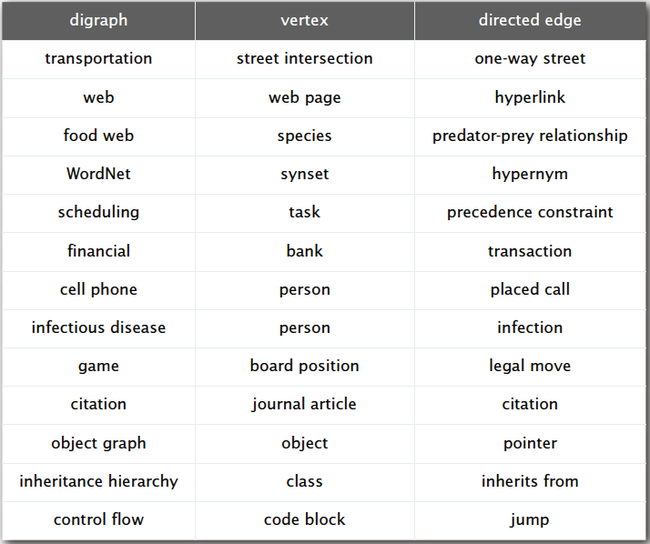
2. Digraph applications :
3. Some digraph problems:
-- Path: Is there a directed path from s to t ?
-- Shortest path: What is the shortest directed path from s to t ?
-- Topological sort: Can you draw a digraph so that all edges point upwards?
-- Strong connectivity: Is there a directed path between all pairs of vertices?
-- Transitive closure: For which vertices v and w is there a path from v to w ?
-- PageRank: What is the importance of a web page?
4. Digraph API:
public class Digraph {
Digraph(int V) {} //create an empty digraph with V vertices
Digraph(In in) {} //create a digraph from input stream
void addEdge(int v, int w) {} //add a directed edge v→w
Iterable<Integer> adj(int v) {} //vertices pointing from v
int V() {} //number of vertices
int E() {} //number of edges
Digraph reverse() {} //reverse of this digraph
String toString() {} //string representation
}
5. Adjacency-lists digraph representation
-- Maintain vertex-indexed array of lists
-- Java implementation
public class Digraph
{
private final int V;
private final Bag<Integer>[] adj;
public Digraph(int V)
{
this.V = V;
adj = (Bag<Integer>[]) new Bag[V];
for (int v = 0; v < V; v++)
adj[v] = new Bag<Integer>();
}
public void addEdge(int v, int w)
{
adj[v].add(w);
}
public Iterable<Integer> adj(int v)
{ return adj[v]; }
}
-- Performance :
6. Depth-first search in digraphs : Same method as for undirected graphs.
-- Every undirected graph is a digraph (with edges in both directions).
-- DFS is a digraph algorithm.
-- Algorithm:
public class DirectedDFS
{
private boolean[] marked;
public DirectedDFS(Digraph G, int s)
{
marked = new boolean[G.V()];
dfs(G, s);
}
private void dfs(Digraph G, int v)
{
marked[v] = true;
for (int w : G.adj(v))
if (!marked[w]) dfs(G, w);
}
public boolean visited(int v)
{ return marked[v]; }
}
7. Reachability application:
-- program control-flow analysis:
1) Every program is a digraph.
-- Vertex = basic block of instructions (straight-line program).
-- Edge = jump.
2) Dead-code elimination.
-- Find (and remove) unreachable code.
3) Infinite-loop detection.
-- Determine whether exit is unreachable.
-- mark-sweep garbage collector:
1) Every data structure is a digraph.
-- Vertex = object.
-- Edge = reference.
2) Roots: Objects known to be directly accessible by program (e.g., stack).
3) Reachable objects: Objects indirectly accessible by program
4) Mark-sweep algorithm:
-- Mark: mark all reachable objects.
-- Sweep: if object is unmarked, it is garbage (so add to free list).
5) Memory cost: Uses 1 extra mark bit per object (plus DFS stack).
8. Breadth-first search in digraphs : Same method as for undirected graphs.
-- Every undirected graph is a digraph (with edges in both directions).
-- BFS is a digraph algorithm.
-- BFS algorithm :

-- BFS computes shortest paths (fewest number of edges) from s to all other vertices in a digraph in time proportional to E + V.
9. Multiple-source shortest paths: Given a digraph and a set of source vertices, find shortest path from any vertex in the set to each other vertex. Solution: use BFS, but initialize by enqueuing all source vertices.
10. Web crawler :
-- Goal: Crawl web, starting from some root web page.
-- Solution:
-- Choose root web page as source s.
-- Maintain a Queue of websites to explore.
-- Maintain a SET of discovered websites.
-- Dequeue the next website and enqueue websites to which it links (provided you haven't done so before).
-- Java Implementation:
Queue<String> queue = new Queue<String>();
SET<String> marked = new SET<String>();
String root = "http://www.princeton.edu";
queue.enqueue(root);
marked.add(root);
while (!queue.isEmpty())
{
String v = queue.dequeue();
StdOut.println(v);
In in = new In(v);
String input = in.readAll();
String regexp = "http://(\\w+\\.)*(\\w+)";
Pattern pattern = Pattern.compile(regexp);
Matcher matcher = pattern.matcher(input);
while (matcher.find())
{
String w = matcher.group();
if (!marked.contains(w))
{
marked.add(w);
queue.enqueue(w);
}
}
}
11. Precedence scheduling :
-- Goal. Given a set of tasks to be completed with precedence constraints, in which order should we schedule the tasks?
-- Digraph model. vertex = task; edge = precedence constraint.
-- Solution : Topological sort : Redraw DAG (Directed Acyclic Graph) so all edges point upwards.
12. Topological sort :
-- Algorithm:
1) Run depth-first search.
2) Return vertices in reverse postorder.
-- Java Implementation:
public class DepthFirstOrder
{
private boolean[] marked;
private Stack<Integer> reversePost;
public DepthFirstOrder(Digraph G)
{
reversePost = new Stack<Integer>();
marked = new boolean[G.V()];
for (int v = 0; v < G.V(); v++)
if (!marked[v]) dfs(G, v);
}
private void dfs(Digraph G, int v)
{
marked[v] = true;
for (int w : G.adj(v))
if (!marked[w]) dfs(G, w);
reversePost.push(v);
}
public Iterable<Integer> reversePost()
{ return reversePost; }
}
-- Proposition. Reverse DFS postorder of a DAG is a topological order.
Pf. Consider any edge v→w. When dfs(v) is called:
-- Case 1: dfs(w) has already been called and returned.
Thus, w was done before v.
-- Case 2: dfs(w) has not yet been called.
dfs(w) will get called directly or indirectly by dfs(v) and will finish before dfs(v).
Thus, w will be done before v.
-- Case 3: dfs(w) has already been called, but has not yet returned.
Can’t happen in a DAG: function call stack contains path from w to v, so v→w would complete a cycle.
13. Proposition. A digraph has a topological order iff no directed cycle.
-- If directed cycle, topological order impossible.
-- If no directed cycle, DFS-based algorithm finds a topological order.
14. Directed cycle detection application :
-- precedence scheduling, a directed cycle implies scheduling problem is infeasible.
-- cyclic inheritance. The Java compiler does cycle detection.
-- spreadsheet recalculation
15. Strongly Connected: Vertices v and w are strongly connected if there is both a directed path
from v to w and a directed path from w to v. Strong connectivity is an equivalence relation:
-- v is strongly connected to v.
-- If v is strongly connected to w, then w is strongly connected to v.
-- If v is strongly connected to w and w to x, then v is strongly connected to x.
A strong component is a maximal subset of strongly-connected vertices.
16. Strong component application :
-- ecological food webs
1) Food web graph. Vertex = species; Edge = from producer to consumer.
2) Strong component. Subset of species with common energy flow.
-- software modules
1) Software module dependency graph. Vertex = software module; Edge: from module to dependency.
2) Strong component. Subset of mutually interacting modules.
3) Usage :
-- Package strong components together.
-- Use to improve design.
16. Kosaraju-Sharir algorithm:
-- Reverse graph: Strong components in G are same as in G-reverse.
-- Kernel DAG: Contract each strong component into a single vertex.
-- Algorithm :
-- Phase 1: run DFS on G-reverse to compute reverse postorder.
-- Phase 2: run DFS on G, considering vertices in order given by first DFS.
-- Java Implementation :
public class KosarajuSharirSCC
{
private boolean marked[];
private int[] id;
private int count;
public KosarajuSharirSCC(Digraph G)
{
marked = new boolean[G.V()];
id = new int[G.V()];
DepthFirstOrder dfs = new DepthFirstOrder(G.reverse());
for (int v : dfs.reversePost())
{
if (!marked[v])
{
dfs(G, v);
count++;
}
}
}
private void dfs(Digraph G, int v)
{
marked[v] = true;
id[v] = count;
for (int w : G.adj(v))
if (!marked[w])
dfs(G, w);
}
public boolean stronglyConnected(int v, int w)
{ return id[v] == id[w]; }
}