数据结构和与算法分析,准备工作
最近开始看数据结构与算法分析,机械工业出版社的。今天刚开始看,刚看完第一章。
惊为天书,实在是太好了,按捺不住激动的心情。为何当初学习数据结构没有如此的激情呢?好了,插一个广告吧,对数据结构感兴趣的,推荐看下。看完这本保证你爱上数据结构,想想现在各个学校学生正在苦读的数据结构教材,也实在是让人痛心,国内啥时候能出几本好书啊。
刚出炉的读书笔记,大家捧捧场。开始正文。
先来两个题目,热热身。
设有一组N个数,要如何确定第k个最大者?
冒泡吧,这个是我的最初的想法,将结果放到数组里,然后找出第k-1个就可以了。这个是最基本的想法了。
稍微好点的,将前k个元素读入数组,并以递减排序,接着将剩下的数字,依次读入,小于第k个则直接忽略,大于就放到响应的位置。
这两个算法是书中给出的,我自己也想了一个其他的。首先可以统计总的数量为多少,如果总数量大于2k。可以取第一个数,以他为基准,对所有的数字进行比较,将大于等于和小于分成两组,并记录两组的数,如果在比较的过程中,大于该数字的数目已经超过k,则直接忽略小于该数字的数,也不用在保存,如果等于k-1则刚好是该数字,至到统计完。如果最后统计结果大于改数的数量大于k,则从大于的组中进行筛选。当然这个方法不是很好,对如何选数字有很强的依赖性和不稳定性。
那种算法好点呢?如果有大量数据,一百万个数字,k=500000,恐怕都很难快速的计算出结果,要若干天才能计算出来,但是在第7章,会给出一个算法,只要1秒就可以给出结果。
卖关子,真想一口气看到第7章。
第二个题目,解决一个流行的猜字谜的游戏。输入一个字母组成的二维数组,找出横,竖,以及斜线方向上的所有的正确的单词组合。
t h i s
w a t s
o a h g
f g d t
这个改如何解决,遍历所有的组合,然后遍历所有的正确的单词?这个方法太土了。而且如果词库是一本字典,那么计算就需要相当可观的时间。不过这样的问题还是有可能在数秒内解决,即使单词表很大。(伏笔)大家想想有啥好办法?

许多问题中,一个重要的观念是,写一个可以运行的程序不难。但是保证这个程序在大的数据集下运行,那么运行时间就成一个很大的问题。我们要学习的就是找到束缚程序速度的瓶颈,并找到合适的方法解决他。
好了这个问题就到这里。复习下数学。
1,常用数学公式。对公式证明感兴趣的同学可以在网上找相关资料。因为数学这些字符不知道怎么搞,只好来图片了。那位同学知道有写数学公式的好工具也介绍下。
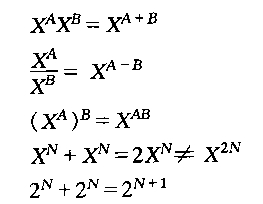
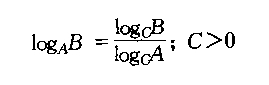
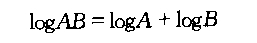
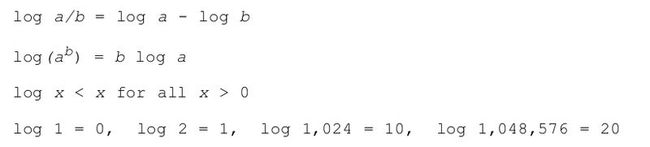
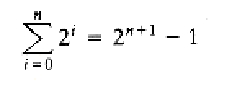

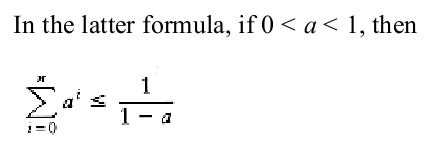
2,模运算。如果A整除B-C,那么B与C模A同余。记作
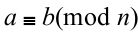
3,证明方法。最常用的有归纳法和反证法。
归纳法有两个部分组成,第一,证明基准情形,就是确定定理对于某个小的值是正确的。第二,归纳假设,如果定理对于k的情况成立,那么对于k+1也应该成立。例子我这里不举了,如果不理解,可以参考高中归纳证明法的方法。
反证法,通过假设定理不成立,然后推导出某个已知的性质不成立。感觉这里有点错误吧。反证法只能证明定理的错误吧,因为只要假设定理正确,然后推导出一个不正确的性质,即可证明定理的错误。反之,恐怕不行吧。这个应该是充分条件和必要条件的差别。这里应该是书本的错误,不知道读过的有没有发现。
来个递归的例子。
我们有个数字,希望他能打印出来,但是我们有这样一个程序print_digit(4),打印4,每次只能打印单个数字。如何实现打印2124呢?
不过并不是一个很好的主意,因为mod运算很消耗很大。N%10=N-[N/10]*10. 原来在学校时都是这么做的,看来完全没有可取性。
原来在学校时都是这么做的,看来完全没有可取性。
递归简论,递归的四大法则:
1,基准情形。必须有基准情形,就是所谓的已知条件。
2,不断推进。每次递归都在朝基准情形靠近。
3,设计法则,假设所有的递归调用都能运行。
一个反例
4,合成效益法则。在求解同一问题的同一实例时,切勿在不同的递归调用中做重复的工作。(不懂,不过这个在后面章节会继续讲解)。
使用递归解决斐波那契数之类的简单数学函数的想法一般不是一个好主意。
总结:设计好的算法,需要学好数学和数据结构。
惊为天书,实在是太好了,按捺不住激动的心情。为何当初学习数据结构没有如此的激情呢?好了,插一个广告吧,对数据结构感兴趣的,推荐看下。看完这本保证你爱上数据结构,想想现在各个学校学生正在苦读的数据结构教材,也实在是让人痛心,国内啥时候能出几本好书啊。
刚出炉的读书笔记,大家捧捧场。开始正文。
先来两个题目,热热身。
设有一组N个数,要如何确定第k个最大者?
冒泡吧,这个是我的最初的想法,将结果放到数组里,然后找出第k-1个就可以了。这个是最基本的想法了。
稍微好点的,将前k个元素读入数组,并以递减排序,接着将剩下的数字,依次读入,小于第k个则直接忽略,大于就放到响应的位置。
这两个算法是书中给出的,我自己也想了一个其他的。首先可以统计总的数量为多少,如果总数量大于2k。可以取第一个数,以他为基准,对所有的数字进行比较,将大于等于和小于分成两组,并记录两组的数,如果在比较的过程中,大于该数字的数目已经超过k,则直接忽略小于该数字的数,也不用在保存,如果等于k-1则刚好是该数字,至到统计完。如果最后统计结果大于改数的数量大于k,则从大于的组中进行筛选。当然这个方法不是很好,对如何选数字有很强的依赖性和不稳定性。
那种算法好点呢?如果有大量数据,一百万个数字,k=500000,恐怕都很难快速的计算出结果,要若干天才能计算出来,但是在第7章,会给出一个算法,只要1秒就可以给出结果。
卖关子,真想一口气看到第7章。
第二个题目,解决一个流行的猜字谜的游戏。输入一个字母组成的二维数组,找出横,竖,以及斜线方向上的所有的正确的单词组合。
t h i s
w a t s
o a h g
f g d t
这个改如何解决,遍历所有的组合,然后遍历所有的正确的单词?这个方法太土了。而且如果词库是一本字典,那么计算就需要相当可观的时间。不过这样的问题还是有可能在数秒内解决,即使单词表很大。(伏笔)大家想想有啥好办法?
许多问题中,一个重要的观念是,写一个可以运行的程序不难。但是保证这个程序在大的数据集下运行,那么运行时间就成一个很大的问题。我们要学习的就是找到束缚程序速度的瓶颈,并找到合适的方法解决他。
好了这个问题就到这里。复习下数学。
1,常用数学公式。对公式证明感兴趣的同学可以在网上找相关资料。因为数学这些字符不知道怎么搞,只好来图片了。那位同学知道有写数学公式的好工具也介绍下。
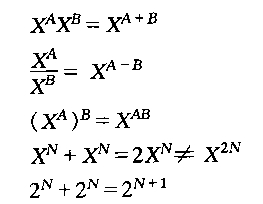
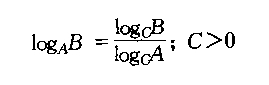
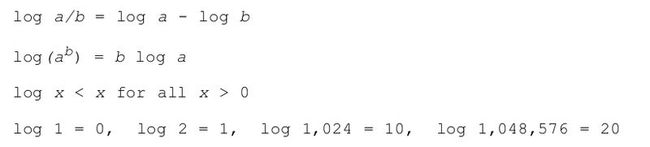
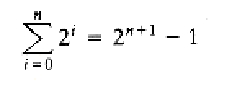

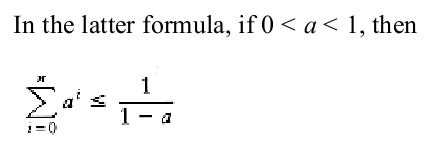
2,模运算。如果A整除B-C,那么B与C模A同余。记作
3,证明方法。最常用的有归纳法和反证法。
归纳法有两个部分组成,第一,证明基准情形,就是确定定理对于某个小的值是正确的。第二,归纳假设,如果定理对于k的情况成立,那么对于k+1也应该成立。例子我这里不举了,如果不理解,可以参考高中归纳证明法的方法。
反证法,通过假设定理不成立,然后推导出某个已知的性质不成立。感觉这里有点错误吧。反证法只能证明定理的错误吧,因为只要假设定理正确,然后推导出一个不正确的性质,即可证明定理的错误。反之,恐怕不行吧。这个应该是充分条件和必要条件的差别。这里应该是书本的错误,不知道读过的有没有发现。
来个递归的例子。
我们有个数字,希望他能打印出来,但是我们有这样一个程序print_digit(4),打印4,每次只能打印单个数字。如何实现打印2124呢?
void print_out( unsigned int n ) /* print nonnegative n */
{
if( n<10 )
print_digit( n );
else
{
print_out( n/10 );
print_digit( n%10 );
}
}
不过并不是一个很好的主意,因为mod运算很消耗很大。N%10=N-[N/10]*10.
递归简论,递归的四大法则:
1,基准情形。必须有基准情形,就是所谓的已知条件。
2,不断推进。每次递归都在朝基准情形靠近。
3,设计法则,假设所有的递归调用都能运行。
一个反例
int bad( unsigned int n )
{
if(n == 0)
return 0
else
return( bad (n/3 + 1) + n - 1 );
}
4,合成效益法则。在求解同一问题的同一实例时,切勿在不同的递归调用中做重复的工作。(不懂,不过这个在后面章节会继续讲解)。
使用递归解决斐波那契数之类的简单数学函数的想法一般不是一个好主意。
总结:设计好的算法,需要学好数学和数据结构。