《算法导论》读书笔记1(算法入门)
学习开发至今,《算法导论》这部经典却一直没有看过。虽然大多常见算法都在其他书籍(如数据结构)学过,但还是想重新把它看一遍。今天终于收到amazon寄来的厚厚的一本,开始看。。。
书共分八部分,其中最后一部分附录,是数学基础。我是先看这一部分的,浏览了一遍。
基本上内容有:
1。高数中的级数,常见的数列(级数)的求和。 --- 基本上用数学归级法很容易证明
2。离散数学中的:集合,关系以及函数,图,树,二叉树概念。
3。概率论的基础知识
接着就是第一部分《基础知识》
第一章是《算法在计算机中的作用》
就我自己认为:算法很重要,他对于计算机来说,可能是速度,但对于我们程序员来说更是“思想”,是“解决之道”。学习和掌握算法以及中间的原理,有助于我们写出更好的程序。
第二章是《算法入门》
本章介绍了两个排序算法,并用伪代码进行描述。进而分析他们的正确性,以及算法复杂度。
主要是让读者熟悉书中的伪代码描述形式,以及分析算法的方法。为其他章节做好准备。
比起看枯燥的分析,我更喜欢写实际的可运行的代码。当我用ruby写完插入排序,发现排10万个数据很累,所以又用java实现。
首先,我写了“插入排序”
public void insertionSort(int[] ary) {
for (int i = 1; i < ary.length; i++) {
int t = ary[i];
int j = i - 1;
while (j >= 0 && ary[j] > t) {
ary[j + 1] = ary[j];
j--;
}
ary[j + 1] = t;
}
}
我需要测试它是否正确, 但是首先得有一个随机数组,于是我又写了一个方法,用于产生随机数组
public int[] genRandAry(int n) {
int[] ary = new int[n];
Random rand = new Random();
for (int i = 0; i < ary.length; i++) {
ary[i] = rand.nextInt();
}
return ary;
}
现在有随机数组,可以进行排序了。但是在排序后,还需要测试一下,是否正确, 自然地我又写了一个方法,用于测试数组是否正确排序。
public boolean isSorted(int[] ary) {
for (int i = 0; i < ary.length - 1; i++) {
if (ary[i] > ary[i + 1]) {
return false;
}
}
return true;
}
万事俱备,测试它吧,我写了一个测试方法,使用junit
@Test
public void testInsertionSort() {
for (int i = 0; i < 1000; ++i) {
int[] ary = genRandAry(i);
insertionSort(ary);
assertTrue(isSorted(ary));
}
}
意料之中,看到绿条。
很久前我就知道插入排序比较差,时间复杂度为平方数量级的,可是还真的没比较过呢, 现在刚好可以试一下。
public void sortManyManyData() {
int[] nums = { 1000, 2000, 5000, 8000,
10000, 20000, 50000, 80000,
100000, 200000, 500000, 800000,
1000000, 2000000, 5000000, 8000000,
10000000};
long[] sortTimes = new long[nums.length];
for (int i = 0; i < nums.length; ++i) {
int k = 10;
long time = 0;
for (int j = 0; j < k; ++j) {
int[] ary = genRandAry(nums[i]);
long begin = Calendar.getInstance().getTimeInMillis();
insertionSort(ary);
//mergeSort(ary);
//Arrays.sort(ary);
long end = Calendar.getInstance().getTimeInMillis();
time += (end - begin);
}
sortTimes[i] = time / k;
}
System.out.println("排序数量\t\t排序时间(ms)");
for (int i = 0; i < nums.length; ++i) {
System.out.println("" + nums[i] + "\t\t" + sortTimes[i]);
}
}
我运行了以上代码,结果做了一个晚餐,他还没运行好,被我强制中断,修改了nums, 让它小一点。 结果排序10万整数时间大约为9秒(更大的我没耐心等了,呼呼)。
然后我用Array.sort也进行排序, 结果排序一千万整数,竟然不到3秒。
先不忙分析复杂度, 因为书中还介绍了另一个算法“归并排序”。我先实现它。 算法也很简单:
public void mergeSort(int[] ary) {
if (ary.length == 0 || ary.length == 1) {
return;
}
int mid = ary.length / 2;
int[] a = Arrays.copyOfRange(ary, 0, mid);
int[] b = Arrays.copyOfRange(ary, mid, ary.length);
mergeSort(a);
mergeSort(b);
merge(a, b, ary);
}
先分割原数组成两个数组,再分别归并排序,最后合并成一个大数组:),当然还有一个merge
private void merge(int[] a, int[] b, int[] ary) {
int i = 0;
int j = 0;
int k = 0;
while (i < a.length && j < b.length) {
if (a[i] <= b[j]) {
ary[k++] = a[i++];
} else {
ary[k++] = b[j++];
}
}
for (; i < a.length; ++i) {
ary[k++] = a[i];
}
for (; j < b.length; ++j) {
ary[k++] = b[j];
}
}
书中用扑克牌形容这个合并过程,挺形像的。“两堆已排好顺序的牌,小的朝上, 我们只要每次拿两堆上面的小的这张, 叠起来,就成了”
同样,我也为它写了个测试代码(就像上面的testInsertionSort 一样)
然后我为它运行上面的 sortManyManyData, 结果当数据量为800万的时候,出现out of memory, 也难怪,因为每一次递归,都要分配同样数组大小的数据空间,不过这个可以进行优化。
排序500万的数据,大概需要 4.8秒,挺快的:)
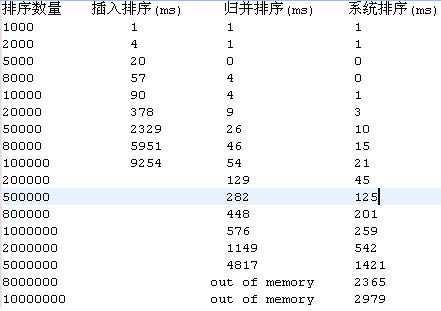
但是和Arrays.sort不能比呀。 下面是排序时间的对比:)
在思考题部分:2-1中“在合并排序中对小数组采用插入排序”。
题外之意是说,在数据量小时,插入排序比归并排序具有更快的速度。
但上面的时间统计,我们看不出这个结论,原因是:因为最小的也是1000个,而再小,我的程序也测试不出时间差别了。
怎么办呢? 我要对排序的基本操作进行统计, 即对它的复杂度进行分析。
不过数学分析挺累的, 还是代码比较容易:)
先从“插入排序”开始分析:
原来的代码是这样的:
public void insertionSort(int[] ary) {
for (int i = 1; i < ary.length; i++) {
int t = ary[i];
int j = i - 1;
while (j >= 0 && ary[j] > t) {
ary[j + 1] = ary[j];
j--;
}
ary[j + 1] = t;
}
}
我想统计基本操作的次数
于是,代码首先被我重构成这样:(灵感来源于 beautiful code, 书中对quicksort进行类似的分析)
public int insertionSort2(int[] ary) {
int times = 0; // add
for (int i = 1; i < ary.length; i++) {
int t = ary[i];
int j = i - 1;
while (j >= 0 && ary[j] > t) {
ary[j + 1] = ary[j];
j--;
times++; // add
}
ary[j + 1] = t;
}
return times; // add
}
看代码注释部分(奇怪,语法加亮怎么不行了)
继续重构, 我们考虑最坏的情况,即 while 中的测试: ary[j] > t 全为false,这时候比较和移动次数最多, 那我们去掉它
public int insertionSort2(int[] ary) {
int times = 0;
for (int i = 1; i < ary.length; i++) {
int t = ary[i];
int j = i - 1;
while (j >= 0 /*&& ary[j] > t*/) { // remove
ary[j + 1] = ary[j];
j--;
times++;
}
ary[j + 1] = t;
}
return times;
}
既然我们现在只是统计次数,那么关于移动数组元素的无关操作也可以去掉
public int insertionSort2(int[] ary) {
int times = 0;
for (int i = 1; i < ary.length; i++) {
int j = i - 1;
while (j >= 0) {
j--;
times++;
}
}
return times;
}
再变换一下:
public int insertionSort2(int n) {
int times = 0;
for (int i = 1; i < n; i++) {
//j = i - 1;
//while (j >= 0) {
// j--;
// times++;
//}
times += i;
}
return times;
}
再改一下:
public int insertionSort2(int n) {
int times = 0;
//for (int i = 1; i < n; i++) {
// times += i;
//}
//so times = 1 + 2 + 3 + ... + (n - 1);
times = (1 + n - 1) * (n - 1) / 2;
return times;
}
最后:
public int insertionSort2(int n) {
return n * (n - 1) / 2;
}
写起来多,其实在编辑器上,只需要几步就成, 比单独在脑子中想,或者用笔在纸上画,不容易出错。而且简单很多:)
上面是最复杂的情况,其实平均情况下。while 中只要做 i / 2 次。
所以平均比较次数会是这样: n * (n - 1) / 4
下面同样对mergeSort 进行分析:)
原来的mergeSort代码是这样的:
public void mergeSort(int[] ary) {
if (ary.length == 0 || ary.length == 1) {
return;
}
int mid = ary.length / 2;
int[] a = Arrays.copyOfRange(ary, 0, mid);
int[] b = Arrays.copyOfRange(ary, mid, ary.length);
mergeSort(a);
mergeSort(b);
merge(a, b, ary);
}
重构一下成这样:
public intmergeSort2(int[] ary) {
if (ary.length == 0 || ary.length == 1) {
return 0; // modify
}
int times = 0; // add
int mid = ary.length / 2;
int[] a = Arrays.copyOfRange(ary, 0, mid);
int[] b = Arrays.copyOfRange(ary, mid, ary.length);
times += mergeSort2(a); // modify
times += mergeSort2(b); // modify
//times += merge过程比较次数
return times;
}
上面的比较次数来源于两个递归调用的 mergeSort 以及一个merge
想一下, merge是合并过程。比如有n张牌分成两堆(排序好的)进行归并,每次拿走一张牌(比较一次,要是一堆拿完了,就不需要比较了),所以最多比较 n - 1次,就完成归并过程
而且如果 n 是偶数的话 mergeSort2(a) = mergeSort2(b)
而且我们对数组本身不感兴趣。只对数组大小感兴趣。
public int mergeSort2(int n) {
if (n == 0 || n == 1) {
return 0;
}
int times = 0;
times += 2 * mergeSort2(n / 2);
times += n - 1;
return times;
}
再简化一下:
public int mergeSort2(int n) {
if (n == 0 || n == 1) {
return 0;
}
return 2 * mergeSort2(n / 2) + n - 1;
}
上面这个方法就是用来求归并排序的比较次数的
然后我们回到原来的问题: 啥时候 插入排序可能会比归并排序要快呢?
我写了下面的代码
public void campareTimes() {
int i = 0;
while (true) {
int t1 = insertionSort3(i); // n * (n - 1) / 4 使用平均比较次数
int t2 = mergeSort2(i);
System.out.println("" + i + "\t\t" + t1 + "\t\t" + t2);
if (t1 > t2) {
break;
}
i++;
}
}
输出这样的:
元素个数 插入排序(比较次数) 归并排序(比较次数) 0 0 0 1 0 0 2 0 1 3 1 2 4 3 5 5 5 6 6 7 9 7 10 10 8 14 17 9 18 18 10 22 21
可以看出,当元素少于9个时, 插入排序会比归并排序比较次数来得少。
好像少得不多呀。平均只差2, 可是如果对一千万个数据归并, 当分解到小于9个时(假设此时是8), 使用插入排序代替归并排序。
那么应该相差 (1000 0000 / 8) * 3 = 375 0000
那也挺可观的:)
Arrays.sort 很快。文档写着:
使用的是快速排序, 等我看到快递排序这章时,写一个再比较一下:)