集合框架 Map篇(5)----ConcurrentSkipListMap
Map
------
1.HashMap
2.LinkedHashMap
3.IdentityHashMap
4.WeakHashMap
5.TreeMap
6.EnumMap
7.ConcurrentHashMap
8.ConcurrentSkipListMap
--------------------------------------
------------------ConcurrentSkipListMap-----------------
ConcurrentSkipListMap提供了一种线程安全的并发访问的排序映射表。内部是SkipList(跳表)结构实现,在理论上能够在O(log(n))时间内完成查找、插入、删除操作。
SkipList是一种红黑树的替代方案,由于SkipList与红黑树相比无论从理论和实现都简单许多,所以得到了很好的推广。SkipList是基于一种统计学原理实现的,有可能出现最坏情况,即查找和更新操作都是O(n)时间复杂度,但从统计学角度分析这种概率极小。
使用SkipList类型的数据结构更容易控制多线程对集合访问的处理,因为链表的局部处理性比较好,当多个线程对SkipList进行更新操作(指插入和删除)时,SkipList具有较好的局部性,每个单独的操作,对整体数据结构影响较小。而如果使用红黑树,很可能一个更新操作,将会波及整个树的结构,其局部性较差。因此使用SkipList更适合实现多个线程的并发处理。
在非多线程的情况下,应当尽量使用TreeMap。此外对于并发性相对较低的并行程序可以使用Collections.synchronizedSortedMap将TreeMap进行包装,也可以提供较好的效率。对于高并发程序,应当使用ConcurrentSkipListMap,能够提供更高的并发度。
所以在多线程程序中,如果需要对Map的键值进行排序时,请尽量使用ConcurrentSkipListMap,可能得到更好的并发度。
注意,调用ConcurrentSkipListMap的size时,由于多个线程可以同时对映射表进行操作,所以映射表需要遍历整个链表才能返回元素个数,这个操作是个O(log(n))的操作。
ConcurrentSkipListMap存储结构

ConcurrentSkipListMap存储结构图
跳跃表(SkipList):(如上图所示)
1.多条链构成,是关键字升序排列的数据结构;
2.包含多个级别,一个head引用指向最高的级别,最低(底部)的级别,包含所有的key;
3.每一个级别都是其更低级别的子集,并且是有序的;
4.如果关键字 key在 级别level=i中出现,则,level<=i的链表中都会包含该关键字key;
------------------------
ConcurrentSkipListMap主要用到了Node和Index两种节点的存储方式,通过volatile关键字实现了并发的操作
------------------------
ConcurrentSkipListMap的查找
通过SkipList的方式进行查找操作:(下图以“查找91”进行说明:)

红色虚线,表示查找的路径,蓝色向右箭头表示right引用;黑色向下箭头表示down引用;
ConcurrentSkipListMap的删除
通过SkipList的方式进行删除操作:(下图以“删除23”进行说明:)

红色虚线,表示查找的路径,蓝色向右箭头表示right引用;黑色向下箭头表示down引用;
ConcurrentSkipListMap的插入
通过SkipList的方式进行插入操作:(下图以“添加55”的两种情况,进行说明:)

在level=2(该level存在)的情况下添加55的图示:只需在level<=2的合适位置插入55即可
--------
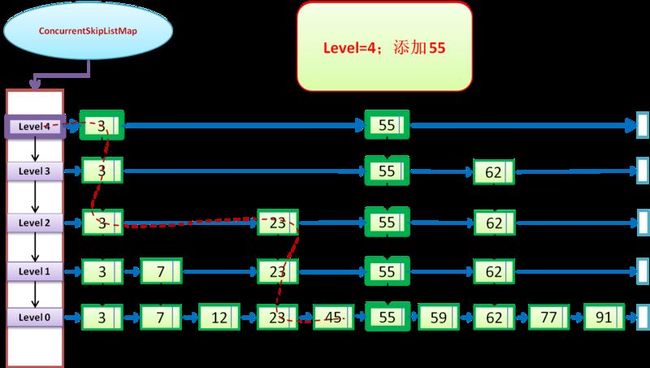
在level=4(该level不存在,图示level4是新建的)的情况下添加55的情况:首先新建level4,然后在level<=4的合适位置插入55
-----------
------
1.HashMap
2.LinkedHashMap
3.IdentityHashMap
4.WeakHashMap
5.TreeMap
6.EnumMap
7.ConcurrentHashMap
8.ConcurrentSkipListMap
--------------------------------------
------------------ConcurrentSkipListMap-----------------
ConcurrentSkipListMap提供了一种线程安全的并发访问的排序映射表。内部是SkipList(跳表)结构实现,在理论上能够在O(log(n))时间内完成查找、插入、删除操作。
SkipList是一种红黑树的替代方案,由于SkipList与红黑树相比无论从理论和实现都简单许多,所以得到了很好的推广。SkipList是基于一种统计学原理实现的,有可能出现最坏情况,即查找和更新操作都是O(n)时间复杂度,但从统计学角度分析这种概率极小。
使用SkipList类型的数据结构更容易控制多线程对集合访问的处理,因为链表的局部处理性比较好,当多个线程对SkipList进行更新操作(指插入和删除)时,SkipList具有较好的局部性,每个单独的操作,对整体数据结构影响较小。而如果使用红黑树,很可能一个更新操作,将会波及整个树的结构,其局部性较差。因此使用SkipList更适合实现多个线程的并发处理。
在非多线程的情况下,应当尽量使用TreeMap。此外对于并发性相对较低的并行程序可以使用Collections.synchronizedSortedMap将TreeMap进行包装,也可以提供较好的效率。对于高并发程序,应当使用ConcurrentSkipListMap,能够提供更高的并发度。
所以在多线程程序中,如果需要对Map的键值进行排序时,请尽量使用ConcurrentSkipListMap,可能得到更好的并发度。
注意,调用ConcurrentSkipListMap的size时,由于多个线程可以同时对映射表进行操作,所以映射表需要遍历整个链表才能返回元素个数,这个操作是个O(log(n))的操作。
ConcurrentSkipListMap存储结构

ConcurrentSkipListMap存储结构图
跳跃表(SkipList):(如上图所示)
1.多条链构成,是关键字升序排列的数据结构;
2.包含多个级别,一个head引用指向最高的级别,最低(底部)的级别,包含所有的key;
3.每一个级别都是其更低级别的子集,并且是有序的;
4.如果关键字 key在 级别level=i中出现,则,level<=i的链表中都会包含该关键字key;
------------------------
ConcurrentSkipListMap主要用到了Node和Index两种节点的存储方式,通过volatile关键字实现了并发的操作
static final class Node<K,V> {
final K key;
volatile Object value;//value值
volatile Node<K,V> next;//next引用
……
}
static class Index<K,V> {
final Node<K,V> node;
final Index<K,V> down;//downy引用
volatile Index<K,V> right;//右边引用
……
}
------------------------
ConcurrentSkipListMap的查找
通过SkipList的方式进行查找操作:(下图以“查找91”进行说明:)

红色虚线,表示查找的路径,蓝色向右箭头表示right引用;黑色向下箭头表示down引用;
/get方法,通过doGet操作实现
public V get(Object key) {
return doGet(key);
}
//doGet的实现
private V doGet(Object okey) {
Comparable<? super K> key = comparable(okey);
Node<K,V> bound = null;
Index<K,V> q = head;//把头结点作为当前节点的前驱节点
Index<K,V> r = q.right;//前驱节点的右节点作为当前节点
Node<K,V> n;
K k;
int c;
for (;;) {//遍历
Index<K,V> d;
// 依次遍历right节点
if (r != null && (n = r.node) != bound && (k = n.key) != null) {
if ((c = key.compareTo(k)) > 0) {//由于key都是升序排列的,所有当前关键字大于所要查找的key时继续向右遍历
q = r;
r = r.right;
continue;
} else if (c == 0) {
//如果找到了相等的key节点,则返回该Node的value如果value为空可能是其他并发delete导致的,于是通过另一种
//遍历findNode的方式再查找
Object v = n.value;
return (v != null)? (V)v : getUsingFindNode(key);
} else
bound = n;
}
//如果一个链表中right没能找到key对应的value,则调整到其down的引用处继续查找
if ((d = q.down) != null) {
q = d;
r = d.right;
} else
break;
}
// 如果通过上面的遍历方式,还没能找到key对应的value,再通过Node.next的方式进行查找
for (n = q.node.next; n != null; n = n.next) {
if ((k = n.key) != null) {
if ((c = key.compareTo(k)) == 0) {
Object v = n.value;
return (v != null)? (V)v : getUsingFindNode(key);
} else if (c < 0)
break;
}
}
return null;
}------------------------------------------------
ConcurrentSkipListMap的删除
通过SkipList的方式进行删除操作:(下图以“删除23”进行说明:)

红色虚线,表示查找的路径,蓝色向右箭头表示right引用;黑色向下箭头表示down引用;
//remove操作,通过doRemove实现,把所有level中出现关键字key的地方都delete掉
public V remove(Object key) {
return doRemove(key, null);
}
final V doRemove(Object okey, Object value) {
Comparable<? super K> key = comparable(okey);
for (;;) {
Node<K,V> b = findPredecessor(key);//得到key的前驱(就是比key小的最大节点)
Node<K,V> n = b.next;//前驱节点的next引用
for (;;) {//遍历
if (n == null)//如果next引用为空,直接返回
return null;
Node<K,V> f = n.next;
if (n != b.next) // 如果两次获得的b.next不是相同的Node,就跳转到第一层循环重新获得b和n
break;
Object v = n.value;
if (v == null) { // 当n被其他线程delete的时候,其value==null,此时做辅助处理,并重新获取b和n
n.helpDelete(b, f);
break;
}
if (v == n || b.value == null) // 当其前驱被delet的时候直接跳出,重新获取b和n
break;
int c = key.compareTo(n.key);
if (c < 0)
return null;
if (c > 0) {//当key较大时就继续遍历
b = n;
n = f;
continue;
}
if (value != null && !value.equals(v))
return null;
if (!n.casValue(v, null))
break;
if (!n.appendMarker(f) || !b.casNext(n, f))//casNext方法就是通过比较和设置b(前驱)的next节点的方式来实现删除操作
findNode(key); // 通过尝试findNode的方式继续find
else {
findPredecessor(key); // Clean index
if (head.right == null) //如果head的right引用为空,则表示不存在该level
tryReduceLevel();
}
return (V)v;
}
}
}-------------------------------------
ConcurrentSkipListMap的插入
通过SkipList的方式进行插入操作:(下图以“添加55”的两种情况,进行说明:)

在level=2(该level存在)的情况下添加55的图示:只需在level<=2的合适位置插入55即可
--------

在level=4(该level不存在,图示level4是新建的)的情况下添加55的情况:首先新建level4,然后在level<=4的合适位置插入55
-----------
//put操作,通过doPut实现
public V put(K key, V value) {
if (value == null)
throw new NullPointerException();
return doPut(key, value, false);
}
private V doPut(K kkey, V value, boolean onlyIfAbsent) {
Comparable<? super K> key = comparable(kkey);
for (;;) {
Node<K,V> b = findPredecessor(key);//前驱
Node<K,V> n = b.next;
//定位的过程就是和get操作相似
for (;;) {
if (n != null) {
Node<K,V> f = n.next;
if (n != b.next) // 前后值不一致的情况下,跳转到第一层循环重新获得b和n
break;;
Object v = n.value;
if (v == null) { // n被delete的情况下
n.helpDelete(b, f);
break;
}
if (v == n || b.value == null) // b 被delete的情况,重新获取b和n
break;
int c = key.compareTo(n.key);
if (c > 0) {
b = n;
n = f;
continue;
}
if (c == 0) {
if (onlyIfAbsent || n.casValue(v, value))
return (V)v;
else
break; // restart if lost race to replace value
}
// else c < 0; fall through
}
Node<K,V> z = new Node<K,V>(kkey, value, n);
if (!b.casNext(n, z))
break; // restart if lost race to append to b
int level = randomLevel();//得到一个随机的level作为该key-value插入的最高level
if (level > 0)
insertIndex(z, level);//进行插入操作
return null;
}
}
}
/**
* 获得一个随机的level值
*/
private int randomLevel() {
int x = randomSeed;
x ^= x << 13;
x ^= x >>> 17;
randomSeed = x ^= x << 5;
if ((x & 0x8001) != 0) // test highest and lowest bits
return 0;
int level = 1;
while (((x >>>= 1) & 1) != 0) ++level;
return level;
}
//执行插入操作:如上图所示,有两种可能的情况:
//1.当level存在时,对level<=n都执行insert操作
//2.当level不存在(大于目前的最大level)时,首先添加新的level,然后在执行操作1
private void insertIndex(Node<K,V> z, int level) {
HeadIndex<K,V> h = head;
int max = h.level;
if (level <= max) {//情况1
Index<K,V> idx = null;
for (int i = 1; i <= level; ++i)//首先得到一个包含1~level个级别的down关系的链表,最后的inx为最高level
idx = new Index<K,V>(z, idx, null);
addIndex(idx, h, level);//把最高level的idx传给addIndex方法
} else { // 情况2 增加一个新的级别
level = max + 1;
Index<K,V>[] idxs = (Index<K,V>[])new Index[level+1];
Index<K,V> idx = null;
for (int i = 1; i <= level; ++i)//该步骤和情况1类似
idxs[i] = idx = new Index<K,V>(z, idx, null);
HeadIndex<K,V> oldh;
int k;
for (;;) {
oldh = head;
int oldLevel = oldh.level;
if (level <= oldLevel) { // lost race to add level
k = level;
break;
}
HeadIndex<K,V> newh = oldh;
Node<K,V> oldbase = oldh.node;
for (int j = oldLevel+1; j <= level; ++j)
newh = new HeadIndex<K,V>(oldbase, newh, idxs[j], j);//创建新的
if (casHead(oldh, newh)) {
k = oldLevel;
break;
}
}
addIndex(idxs[k], oldh, k);
}
}
/**
*在1~indexlevel层中插入数据
*/
private void addIndex(Index<K,V> idx, HeadIndex<K,V> h, int indexLevel) {
// insertionLevel 代表要插入的level,该值会在indexLevel~1间遍历一遍
int insertionLevel = indexLevel;
Comparable<? super K> key = comparable(idx.node.key);
if (key == null) throw new NullPointerException();
// 和get操作类似,不同的就是查找的同时在各个level上加入了对应的key
for (;;) {
int j = h.level;
Index<K,V> q = h;
Index<K,V> r = q.right;
Index<K,V> t = idx;
for (;;) {
if (r != null) {
Node<K,V> n = r.node;
// compare before deletion check avoids needing recheck
int c = key.compareTo(n.key);
if (n.value == null) {
if (!q.unlink(r))
break;
r = q.right;
continue;
}
if (c > 0) {
q = r;
r = r.right;
continue;
}
}
if (j == insertionLevel) {//在该层level中执行插入操作
// Don't insert index if node already deleted
if (t.indexesDeletedNode()) {
findNode(key); // cleans up
return;
}
if (!q.link(r, t))//执行link操作,其实就是inset的实现部分
break; // restart
if (--insertionLevel == 0) {
// need final deletion check before return
if (t.indexesDeletedNode())
findNode(key);
return;
}
}
if (--j >= insertionLevel && j < indexLevel)//key移动到下一层level
t = t.down;
q = q.down;
r = q.right;
}
}
}