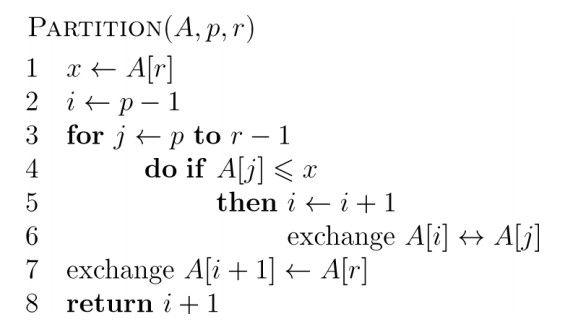【算法导论】排序 (三):快速排序 深入分析
五、快速排序
快速排序是最常用的一种排序算法,包括C的qsort,C++和Java的sort,都采用了快排(C++和Java的sort经过了优化,还混合了其他排序算法)。
快排最坏情况O( n^2 ),但平均效率O(n lg n),而且这个O(n lg n)几号中隐含的常数因子很小,快排可以说是最快的排序算法,并非浪得虚名。另外它还是就地排序。
快速排序是基于分治模式的:
分解:数组A【p..r】被划分成两个(可能空)子数组A【p..q-1】和A【q+1..r】,使得A【p..q-1】中的每个元素都小于等于A(q),而且,小于等于A【q+1..r】中的元素。下 标q 也在返个划分过程中迕行计算。
解决:通过递归调用快速排序,对子数组A【p..q-1】和A【q+1..r】排序。
合并:因为两个子数组使就地排序的,将它们的合并不需要操作:整个数组A【p..r】已排序。
下面过程实现快速排序:
数组划分:Partition(关键,它对子数组A【p..r】进行就地重排)
C++实现:
//* 算法导论 第七章 快速排序 *//
#include<cstdio>
#include<ctime>
#include<cstdlib>
void Swap(int &a,int &b){ if(a!=b){a^=b;b^=a;a^=b;} } //如果两个数相等,就不执行位运算交换。因为如果两数相等,结果会是0
int Partition(int *A,int p,int r){
int x, i;
x=A[r];
i=p-1;
for(int j=p; j<=r-1; ++j){
if(A[j]<=x) {
Swap(A[++i], A[j]);
}
}
Swap(A[++i],A[r]);
return i;
}
void QuickSort(int *A,int p,int r){
if(p<r){
int q=Partition(A,p,r);
QuickSort(A,p,q-1);
QuickSort(A,q+1,r);
}
}
int main()
{
int arr[12]={2,7,4,9,8,5,7,8,2,0,7,-4};
QuickSort(arr,0,11);
for(int i=0; i<12; ++i)
printf("%d ",arr[i]);
putchar('\n');
return 0;
}
快排的性能分析:
当数据量很小的时候,大概就十来个元素的小型序列,快排的优势并不明显,甚至比插入排序慢。但是一旦数据多,它的优势就充分发挥出来了。
举一个例子,C++ STL 中的sort函数,就充分发挥了快排的优势,并且取长补短,在数据量大时采用QuickSort,分段递归排序。一旦分段后的数据量小于某个门槛,为避免QuickSort递归调用带来过大的额外负荷,就改用插入排序。如果递归层次过深,还会改用HeapSort(堆排序)。所以说,C++的“混合兵种”sort的性能肯定会比C的qsort好。
快排的运行时间与Partition的划分有关
最坏情况是输入的数组已经完全排好序,那么每次划分的左、右两个区域分别为n-1和0,效率为O( n^2 ).
而对于其他常数比例划分,哪怕是左右按9:1的比例划分,效果都是和在正中间划分一样快的(算法导论上有详细分析)
即,任何一种按照常数比例进行划分,总运行时间都是O(n lg n).
快排的随机化版本:
因为快排中Partition所产生的划分中可能会有”差的“,而划分的关键在于主元A【r】的选择。我们可以采用一种不同的、称为随机取样的随机化技术,把主元A【r】和A【p..r】中随机选出一个元素交换,这样相当于,我们的主元不在是固定是最后一个A【r】,而是随机从p,...,r这一范围随机取样。 这样可以使得期望平均情况下,Partition的划分能够比较对称.
伪代码的实现 :
C++实现:
int Random(int m,int n){
srand((unsigned)time(NULL)); // 包含头文件<cstdlib>
return m+(rand()%(n-m+1));
}
int Random_Partition(int *A,int p,int r){
int i=Random(p,r);
Swap(A[r],A[i]);
return Partition(A,p,r);
}
void Random_QuickSort(int *A,int p,int r){
if(p<r){
int q=Random_Partition(A,p,r);
Random_QuickSort(A,p,q-1);
Random_QuickSort(A,q+1,r);
}
}
快排的进一步优化的讨论:
1、尾递归:
传统的递归算法在很多时候被视为洪水猛兽. 它的名声狼籍, 好像永远和低效联系在一起,尾递归是极其重要的,不用尾递归,函数的堆栈耗用难以估量,需要保存很多中间函数的堆栈。
快排中的堆栈深度:
QUICKSORT算法包含两个对其自身的递归调用,即调用PARTITION后,左边的子数组和右边的子数组分别被递归排序。QUICKSORT中的第二次递归调用并不是必须的,可以用迭代控制结构来代替它,这种技术叫做“尾递归”,大多数的编译器也使用了这项技术
下面这个版本模拟了尾递归:
QUICKSORT'(A, p, r)
1 while p < r
2 do▸Partition and sort left subarray.
3 q ← PARTITION(A, p, r)
4 QUICKSORT'(A, p, q - 1)
5 p ← q + 1
需要注意第一行是 while而不是if
但是这个版本在最坏的情况下,就是划分不好的时候,递归深度为O(n),可以再进一步优化使栈深度为O(lg n)吗?
用二分的思想,为了使最坏情况下栈的深度为Θ(lgn),我们必须是PARTITION后左边的子数组为原来数组的一半大小,这样递归的深度最多为Θ(lgn)。
一种可能的算法是:首先求得(A, p, r)的中位数,作为PARTITION的枢轴元素,这样可以保证左右两边的元素的个数尽可能的均衡。
因为求中位数的过程MEDIAN的时间复杂度为Θ(n),因此可以保证算法的期望的时间复杂度O(nlgn)不变。
优化版的尾递归快排:
2. "三数取中"划分
所谓“三数取中”是指,从子数组中随机选出三个元素,取其中间数作为主元,这算是前面随机化版本的升级版。虽然是升级版,但是也只能影响快速排序时间复杂度O(nlgn)的常数因子.
下面将给出综合了”优化的尾递归“+”三数取中“版本的Final 快排版本:
// 优化的尾递归 + 三数取中 版本快排
#include<cstdio>
#include<ctime>
#include<cstdlib>
void Swap(int &a,int &b){ if(a!=b){a^=b;b^=a;a^=b;} } //如果两个数相等,就不执行位运算交换。因为如果两数相等,结果会是0
int Partition(int *A,int p,int r){
int x, i;
x=A[r];
i=p-1;
for(int j=p; j<=r-1; ++j){
if(A[j]<=x) {
Swap(A[++i], A[j]);
}
}
Swap(A[++i],A[r]);
return i;
}
inline int Random(int m,int n){
srand((unsigned)time(NULL));
return m+(rand()%(n-m+1));
}
// 取出三个数的中间数(第二大的数)的函数
inline int MidNum(int a,int b,int c){
if(c<b) Swap(c,b);
if(b<a) Swap(b,a); // 经过这两个交换,a变成三数最小的
return b<c?b:c;
}
int ThreeOne_Partition(int *A,int p,int r){
int i,j,k,mid;
// 随机选择三个数
i=Random(p,r);
j=Random(p,r);
k=Random(p,r);
// 取出“中间数”
mid=MidNum(A[i],A[j],A[k]);
// 将“中间数”和A【r】交换
if(A[i]==mid) Swap(A[i],A[r]);
else if(A[j]==mid) Swap(A[j],A[r]);
else if(A[k]==mid) Swap(A[k],A[r]);
return Partition(A,p,r);
}
void Final_QuickSort(int *A,int p,int r){
while(p<r){
int q=ThreeOne_Partition(A,p,r);
if(q-p<r-q){
Final_QuickSort(A,p,q-1);
p=q+1;
}
else{
Final_QuickSort(A,q+1,r);
r=q-1;
}
}
}
int main()
{
int arr[12]={2,7,4,9,8,5,7,8,2,0,7,-4};
Final_QuickSort(arr,0,11);
for(int i=0; i<12; ++i)
printf("%d ",arr[i]);
putchar('\n');
return 0;
}
除此之外,快排还可以有优化:
非递归的方法:即模拟递归,这样可以完全消去递归的调用。
三划分快速排序:基本思想是,在划分阶段以V=A[r]为基准,将带排序数组A【p..r】划分为左、中、右三段A【p,j】,
A【j+1..q-1】,A【q..r】,其中左段数组元素值小于V,中断数组等于V,有段数组元素大于V。其后,算法对左右
两段数组递归排序。 这个方法对于有大量相同数据的数组排序效率有很大的提高,即使没有大量相同元素,也不
降低原快排算法的效率。
以上两种以后有机会再把代码实现一遍吧。
快速排序的总结到这里结束。
目前主要总结了五大排序,都是基于比较的排序,最快也只有O(n lg n)。有没有更快的?
下一篇将总结线性时间排序,其速度将会突破这个瓶颈。
本人只是个小菜鸟,如果错误,希望指出,谢谢
—— 生命的意义,在于赋予它意义。