谈谈快速排序
众所周知,排序在计算机科学的各个方面被作为一个很基础的处理问题的手段广泛应用着——例如查找的时候我们如果拥有的是有序列的话,那查找的时候用二分查找我们就倍感顺利、快速,而要获得有序列,我们首先就得对待查找序列进行排序;又例如,计算机的内存进行分配的过程中有各种方案,其中一种便是遍历可用内存,找到第一个大于等于所需内存大小的内存块,分配相应内存供使用,而为了让遍历的过程更为快速,或者说让获得内存块的时间尽量短,我们便希望维护一个按可用内存块大小进行降序排序的内存块索引表,当我们分配内存的时候总是获得最大的可用内存块的地址,从而我们总是在第一时间能够从最大的可用内存快里面分配所需内存大小,而为了维护这个降序的可用内存索引表,我们在内存的分配的过程中就必须对内存表进行内存大小为主键的排序操作;再如,我们做web服务器的页面cache服务,那我们就必须在web服务器数据库内部的某表中对页面的请求频度进行记录,而且按该频度对页面进行降序的排序,从而让访问频度高的页面能够被缓存到cache服务器中,而为了维护这个应cache页面的表,我们就必须定期对该表项目按频度为主键进行降序排序,从而获得应该做缓存的页面。相应的例子还有很多。
可以比较武断的说,由于排序的需求广泛存在,它已经成为了计算机科学中的一个“永恒的话题”。
谁发明了一个比现有最优排序算法更优的新排序算法,那他必将名垂青史!
呵呵,我觉得我很难会成为那种对某些方面进行质变影响的先驱类人物——至少现在不可能。我能做的,应该还仅仅局限于站在巨人们的肩膀上给他们抓抓虱子。
今天我就抓抓东尼·霍尔的虱子——他的快速排序。
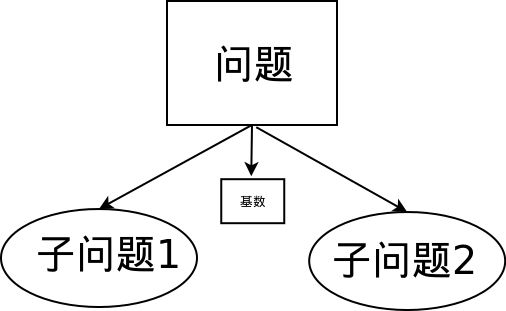
如果你是个还没有进行简单的算法学习的朋友,也先别急,我们先看看下面这个很形象的快速排序的图解。
从这个图解中,我们大致可以把快速排序的主体思想以及实现进行抽离:
统领整体算法的思想:
1.大问题划分为小问题,而且保证问题的需求是不变的,可以用相同的方式求解——分治的思想
2.由于可以用相同的方式求解,我们的求解过程可以是对相同的过程进行复用——递归处理
整体上这两种思想是被经常被用在算法设计中的,它们并称为递归与分治。
(打个小岔子)例如很多c语言书上会很不负责任地介绍如下生成fibonacci数列递归分治法:
这里的代码因为递归与分治处理问题时极度简化的问题模型而变得很简单,有人甚至认为其“简洁给力”。然而它却是一种很不负责任的做法,为什么呢?请看这里。
两个具体的实现手段:
1.将排序问题转化为可递归求解的问题类型——这里的转化为,将无序列在最原子的层级上转化为如下的组合形式:
『比基准数小的数集合』 基准数 『比基准数大的数集合』
什么意思呢?让我们看一些例子:
『1,5,2,3』 6 『7,20,10,9,11』
『1,23,11,55,102』 196 『799,210,320,999,221』
以上为比较普通的例子。
最简单的例子(或者说最原子的例子、粒度最小的例子)
『1』 2 『7』
不难看出,这个原子组合就是已经排好序了的。
我们不难发现,任何一个有序列都是由方才介绍的组合形式的最原子例子组成的——也就是说,你将一个有序列进行划分,总是会在最终得到这种最原子例子。换句话说,我们已经制造了一个可以递归进行求解的问题——将无序列递归地转化为上述组合形式。在递归的最底层,也就是组合的处在原子状态(三个数为一组),我们保证每个原子组合都符合上述组合形式。如果每个原子组合都符合上述组合形式,那么这些原子组合放在一起就一定会组成一个有序列。
不难看出,将排序问题转化为此形式后,递归的方式就很好入手了。
2.既然问题已经被转化为适合递归处理的方式了,那下一步就是决定分治的方式。递归处理问题时,免不了问题的就是子问题化——也就是所谓的分治。
从刚才的组合形式我们可以看到一个很直接的处理分治的手段:
1)选取基准数
2)对序列处理,形成『比基准数小的数集合』 基准数 『比基准数大的数集合』的形式
3)将『比基准数小的数集合』和『比基准数大的数集合』看作新形成的子问题,对它们重复1)2)步骤
不得不提的是子问题和父问题的关系。个人认为,之所以称他们为子问题以及父问题,是因为他们自身的性质是一样的,可以用相同的方式处理。例如上述步骤中,刚开始的1)中父问题为“对一个无序列进行基准数划分”,而3)中的子问题则同样也是“对一个无序列进行基准数划分”。
这里子问题和父问题的关系让我联想到了动态规划中的最优子结构的概念。两者有相似的性质:它们要解决的是同一个问题。也有不同的性质:最优子结构还需要子结构有相应的性质(例如“最优解”)要求,这样父结构可以“放心”地使用它的结果从而保证问题的正确解决;而这里的父子问题只是根据同一种规格进行的划分,父问题对子问题的划分没有所谓的性质要求。
既然递归结构搞定了,问题能够被递归解决了,分治方案也决定了,问题可以很好地划分为为递归服务的父子问题结构了,那这个算法基本上就已经实现了80%,接下来如果不出意外的话,可以开始写代码了。下面仅仅贴出网络上很经典的一段c语言实现:
你也许觉得既然代码出来了,那我们点到即止,是时候结束了吧。:-),现在还远远不是结束的时候呢,我们再来在一个更本质的层面上讨论一下快速排序算法。我们讨论的主题是, 快排和二叉排序树的关系。什么?呵呵,是不是有种云里雾里的感觉?别急,我们慢慢道来。首先,先让我们聊聊递归与分治的本质。个人认为,经过递归与分治的处理,一个大问题被分解为树型的结构了。在快速排序的算法中,我们将大问题(整个无序列排序)分解为了一个二叉树形的问题。这个过程用语言描述不是很方便,我们用图来解释。
第一次进行问题转化,找到了基数,并将问题分解为了子问题1和子问题2:
第二次,在子问题上进行进一步的相同操作则会形成如下的问题结构:
继续下去,你就会发现,确实这个问题被划分为了一个二叉树形的结构——很完美的是,它甚至还是一个满的完全二叉树。
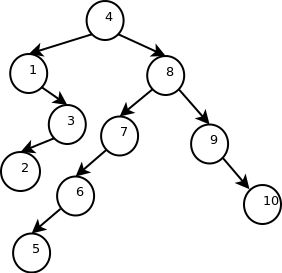
好的,我们在这个思路上再进一步——让我们再考察下在一个实例上进行问题划分后基数的组织形式究竟是什么样的。我们以『2,5,3,6,1,10,9,7,8,4』为例子,选取最后一个数字为基数。那我们最终按照之前的算法进行基数的组织,最后我们得到了基数组成的如下结构:
发现什么了吗?哈哈,这其实本身就是一棵二叉查找树。也就是说,通过快速排序的分治以及递归的处理之后,基数之间存在一个父基数以及子基数的关系,而这个关系结合基数本身的值构成了一个二叉查找树!而与其说快排之后我们按照数列的下标进行遍历就得到了排序好的序列,不如说我们按照基数组成的二叉查找树进行了一次按中序进行的遍历。
怎么样,是不是有一种知识之间骨肉相连的感觉?:-),知识之间总是有各种相连的部分,只要我们去探索,一定会找到一些让我们很惊喜的收获的!