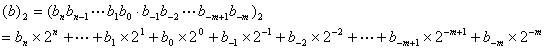Vdsp(bf561)中的浮点运算（5）：float类型表示总结

快乐虾

http://blog.csdn.net/lights_joy/

[email protected]

本文适用于

ADSP-BF561

Visual DSP++ 5.0 (update 6)

欢迎转载，但请保留作者信息

1.1 float的疑问

写一行很简单的C代码：

float a = 1234.56;

用vdsp编译后的汇编代码为：

R0 = 20972 ( X ) ;

R0.H = 17562 ;

[ FP + 0x10 ] = R0 ;

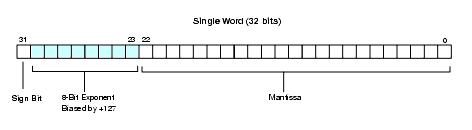
有点看不懂，呵呵，R0的值转换为十六进制就是0x449A51EC。根据vdsp文档的说法，其单精度浮点数格式为：

浮点数计算公式：

将0x449A51EC转换为二进制：

0100 0100 1001 1010 0101 0001 1110 1100

可得：

Sign = 0

Mantissa = 001 1010 0101 0001 1110 1100

Exponent = 1000 1001

按照公式

将Exponent转换为十进制，其值为137。

将Mantissa转换为十进制，其值为：

2^-3 + 2^-4 + 2^-6 + 2^-9 + 2 ^-11 + 2^-15 + 2^-16 + 2^-17 + 2^-18 + 2^-20 + 2^{-21 =}

0.125 + 0.0625 + 0.015625 + 0.001953125 + 0.00048828125 + 0.000030517578125 + 0.0000152587890625 + 0.00000762939453125 + 0.000003814697265625 + 0.00000095367431640625 + 0.000000476837158203125 = 0.205625057220458984375

代入浮点数计算公式：

(-1)⁰ + 1. 205625057220458984375 * 2 ^(137-127)

= 1234.56005859375

那么编译器又是如何将1234.56转换为0x449A51EC的呢？

首先转换整数部分，用2除，取余数，其结果为：

1234 / 2 = 617 ….. 0

617 / 2 = 308 …….1

308 / 2 = 154 …….0

154 / 2 = 77 ……...0

77 / 2 = 38 ……….1

38 / 2 = 19 ……….0

19/ 2 = 9 ………….1

9 / 2 = 4………… .1

4/ 2 = 2 …………..0

2/2 = 1……………0

1/2 = 0……………1

即100 1101 0010，用16进制表示则为：0x4d2。

再转换小数部分，用2乘，取整数位：

0.56 * 2 = 1.12取1

0.12 * 2 = 0.24取0

0.24 * 2 = 0.48取0

0.48 * 2 = 0.96取0

0.96 * 2 = 1.92取1

0.92 * 2 = 1.84取1

0.84 * 2 = 1.68取1

0.68 * 2 = 1.36取1

0.36 * 2 = 0.72取0

0.72 * 2 = 1.44取1

0.44 * 2 = 0.88取0

0.88 * 2 = 1.76取1

0.76 * 2 = 1.52取1

小数部分的值为0.1000 1111 0101 11

所以1234.56表示成二进制数就是

100 1101 0010. 1000 1111 0101 11

由于浮点数表示法的尾数部分以1开头，所以上面的这个数可以表示为：

1.00 1101 0010 1000 1111 0101 11 * 2¹⁰

从浮点数的表示公式即可算出

Exponent = 127 + 10 = 137

而尾数部分则为

00 1101 0010 1000 1111 0101 11

因此整个数就是：

0 1000 1001 00 1101 0010 1000 1111 0101 11

符号位 指数 尾数

从整数的角度来看就是：

0100 0100 1001 1010 0101 0001 1110 1011

十六进制表示为：

4 4 9 A 5 1 E B

奇怪得很，最后居然有偏差。莫非VDSP还有什么机关不成？

1.2 FLT_MIN

FLT_MIN是在float.h中定义的一个常量，用以表示单精度浮点数的最小值。

#define FLT_MIN 1.1754943508222875E-38F

那么这个值从何而来？

从浮点数的表示可以知道，尾数必然是大于等于1的，要取最小值，只能将指数设置为最小值，由于浮点数规定将指数为0的情况表示特殊的浮点数，因此指数只能取1，即

0 00000001 00000000000000000000000

符号位 指数 尾数

从16进制整数看它的值就是 0x00 80 00 00。

根据浮点数的计算公式可知这个值为：

1.0 * 2^-126

= 1.1754943508222875079687365372222e-38

这个是计算器的计算结果。

1.3 FLT_MAX

FLT_MAX是在float.h中定义的一个常量，用以表示单精度浮点数的最大值。

#define FLT_MAX 3.4028234663852886E+38F

那么这个值从何而来？

从浮点数的表示可以知道，要取最大值，可以将指数和尾数都设置为最大值，由于标准规定将指数全为1留做特殊表示，故指数最大值为255，这个数即

0 11111110 11111111111111111111111

符号位 指数 尾数

从16进制整数看它的值就是 0x7f 7f ff ff。

根据浮点数的计算公式可知这个值为：

1. 9999997615814208984375 * 2^(254-127)

= 3.4028234663852886E+38

这个是计算器的计算结果。

1.4 FLT_EPSILON

FLT_EPSILON是在float.h中定义的一个常量，用以表示一个单精度浮点数的最小分辨率，文档对此值的描述是：

A constant that represents the smallest value that may added to 1.0 and still result in a change of value (for example, FLT_EPSILON)

也就是加1后要能看得出变化！

FLT_EPSILON定义为：

#define FLT_EPSILON 1.1920928955078125E-07F

那么这个值从何而来？

先看1.0的浮点表示：

0 01111111 00000000000000000000000

符号位 指数 尾数

从十六进制的角度看就是0x3f80 0000

要想把这个值加上一个足够小的值但仍然能看出变化，当然就是把尾数直接加1，这个数即2^-23，转换成十进制就是FLT_EPSILON的值。

下面是一个很有意思的问题：

float a = FLT_EPSILON;

这个时候a的值会是什么？

在VDSP下试了一下，a的值看成整数是：0x3400 0000，也就是：

0 01101000 00000000000000000000000

符号位 指数 尾数

即1.0 x 2^(104-127) = 1.0 x 2^-23

1.5 INF和NAN

IEEE754规定了单精度浮点数的类型：

Type	Exponent	Fraction	Value
NAN	255	Nonzero	Undefined
Infinity	255	0	(–1)s Infinity
Normal	1 <= e <= 254	Any	(–1)s (1.f22-0) 2 e–127
Zero	0	0	(–1)s Zero

INF的表示要求指数为255，尾数为0，即：

0 11111111 00000000000000000000000

符号位 指数 尾数

也就是0x7f80 0000。

在VDSP下可以用：

float a = 1.0 / 0.0;

来生成一个INF的数。

当然，符号位也可以取负数，即：

1 11111111 00000000000000000000000

符号位 指数 尾数

也就是0xff80 0000。

在VDSP下可以用：

float a = -1.0 / 0.0;

来生成一个-INF的数。

上述两个INF都可以用isinf函数来检测它。

NAN的表示要求指数为255，尾数不为0，即：

0 11111111 00000000000000000000001

符号位 指数 尾数（可取任意不为0的值）

也就是0x7f80 0001这样的数。

在VDSP下可以用：

float a = 0.0 / 0.0;

来生成一个NAN的数，不过这个时候它的值为0xffff ffff。

可以使用isnan函数来检测它。

1 参考资料

Vdsp(bf561)中的浮点运算（4）：FLT_MAX(2009-8-12)

Vdsp(bf561)中的浮点运算（3）：FLT_MIN(2008-12-19)

Vdsp(bf561)中的浮点运算（2）：float的疑问(2008-12-18)

Vdsp(bf561)中的浮点运算（1）：文档的说法(2008-12-16)