Jaro–Winkler distance

From Wikipedia, the free encyclopedia

  (Redirected from  Jaro-Winkler distance)

This article is about the measure. For other uses, see  Jaro.

This article may contain original research. Please improve it by verifying the claims made and adding inline citations. Statements consisting only of original research may be removed. (May 2013)

The topic of this article may not meet Wikipedia's general notability guideline. Please help to establish notability by adding reliable, secondary sources about the topic. If notability cannot be established, the article is likely to be merged, redirected, or deleted. Find sources: "Jaro–Winkler distance" – news · books · scholar · JSTOR · free images (May 2013)

In computer science and statistics, the Jaro–Winkler distance (Winkler, 1990) is a measure of similarity between two strings. It is a variant of the Jaro distance metric (Jaro, 1989, 1995) and mainly^{[citation needed]} used in the area ofrecord linkage (duplicate detection). The higher the Jaro–Winkler distance for two strings is, the more similar the strings are. The Jaro–Winkler distance metric is designed and best suited for short strings such as person names. The score is normalized such that 0 equates to no similarity and 1 is an exact match.

Contents    [hide]  1 Definition 2 Example 3 See also 4 References 5 External links

Definition[edit]

The Jaro distance  of two given strings  and  is

where:

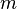•  is the number of matching characters (see below);
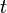•  is half the number of transpositions (see below).

Two characters from  and  respectively, are considered matching only if they are the same and not farther than .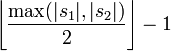

Each character of  is compared with all its matching characters in . The number of matching (but different sequence order) characters divided by 2 defines the number of transpositions. For example. in comparing CRATE with TRACE, only 'R' 'A' 'E' are the matching characters, i.e. m=3. Although 'C', 'T' appear in both strings, they are farther than 1, i.e., floor(5/2)-1=1. Therefore, t=0 . In DwAyNE versus DuANE the matching letters are already in the same order D-A-N-E, so no transpositions are needed.

Jaro–Winkler distance uses a prefix scale  which gives more favourable ratings to strings that match from the beginning for a set prefix length . Given two strings  and , their Jaro–Winkler distance  is:

where:

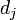•  is the Jaro distance for strings  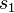and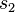 
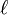•  is the length of common prefix at the start of the string up to a maximum of 4 characters
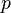•  is a constant scaling factor for how much the score is adjusted upwards for having common prefixes.  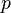should not exceed 0.25, otherwise the distance can become larger than 1. The standard value for this constant in Winkler's work is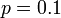 

Although often referred to as a distance metric, the Jaro–Winkler distance is actually not a metric in the mathematical sense of that term because it does not obey the triangle inequality [1].

Example[edit]

Note that Winkler's "reference" C code differs in at least two ways from published accounts of the Jaro–Winkler metric. First is his use of a typo table (adjwt) and also some optional additional tolerance for long strings.

Given the strings  MARTHA and  MARHTA we find:

• 
• 
• 
• There are mismatched characters T/H and H/T leading to 

We find a Jaro score of:

To find the Jaro–Winkler score using the standard weight , we continue to find:

• 

Thus:

Given the strings  DWAYNE and  DUANE we find:

• 
• 
• 
• 

We find a Jaro score of:

To find the Jaro–Winkler score using the standard weight , we continue to find:

• 

Thus:

Given the strings  DIXON and  DICKSONX we find:^{[further explanation needed]}

	D	I	X	O	N
D	1	0	0	0	0
I	0	1	0	0	0
C	0	0	0	0	0
K	0	0	0	0	0
S	0	0	0	0	0
O	0	0	0	1	0
N	0	0	0	0	1
X	0	0	0	0	0

•  Note that the two Xs are not considered matches because they are outside the match window of 3.

• 
• 
• 

We find a Jaro score of:

To find the Jaro–Winkler score using the standard weight , we continue to find:

• 

Thus:

See also[edit]

• Levenshtein distance
• Record linkage
• Census

References[edit]

• Jaro, M. A. (1989). "Advances in record linkage methodology as applied to the 1985 census of Tampa Florida". Journal of the American Statistical Association 84 (406): 414–20. doi:10.1080/01621459.1989.10478785.
• Jaro, M. A. (1995). "Probabilistic linkage of large public health data file". Statistics in Medicine 14 (5–7): 491–8. doi:10.1002/sim.4780140510. PMID 7792443.
• Winkler, W. E. (1990). "String Comparator Metrics and Enhanced Decision Rules in the Fellegi-Sunter Model of Record Linkage". Proceedings of the Section on Survey Research Methods (American Statistical Association): 354–359.

• Winkler, W. E. (2006). "Overview of Record Linkage and Current Research Directions". Research Report Series, RRS.

External links[edit]

• Implementation & documentation in Java LingPipe. Features extensive comparison with the original strcmp.c implementation.
• strcmp.c - Original C Implementation by the author of the algorithm
• PHP implementation released under GPLv3.0
• Open Source implementation in Ruby ported by hand from lucene-3.0.2. (lucene is Java product)
• Open Source implementation in JavaScript as part of a larger project called NaturalNode for natural language processing in Node.js
• Open Source Jaro and Jaro-Winkler Scala implementations as part of the larger stringmetric project
• Open Source implementation in PowerShell

Categories: 

• String similarity measures