5作业树设计原理

 

 

 《树型软件工程方法》之系列博文5

 

作业树设计原理

 

 

 

 

  

 

 

 

   TREESOFT

 

 

 

                      目  录

5 作业树设计原理. 1

5.1 结果倒推法.... 1

5.2 作业子树与问题.... 3

5.2.1 作业子树的物理意义.... 3

5.2.2 作业树的初始型态树.... 4

5.2.3 真问题型态树.... 5

5.3 问题递归处理.... 6

5.4 问题递归实例分析.... 9

5.4.1 冒泡排序问题.... 9

5.4.2 解一元二次方程问题.... 10

5.4.3 二分查找问题.... 11

5.6 结束语.... 12

 

中国人为什么不可以有自己的软件工程方法及其开发工具平台！

这是介绍《树型软件工程方法》的系列博文，请按文章标题所带的编号顺序阅读，否则你会看不懂本文。

 

5 作业树设计原理           

我们已经完成了对作业树相关概念的叙述，给出了按照问题求解算法设计作业树的方法，并且有过四个设计实例。然而，问题求解算法为什么能表示成作业树呢？这就涉及到作业树的设计原理，本文将对此进行讨论和分析。本文的内容很有趣，叙述也颇具艺术性。同时，本文的新概念比较多，分析求证过程也挺烦人。所以，阅读本文不仅要求熟悉作业树的相关概念，也还需要有点耐心，慢慢咀嚼评味。

 

5.1 结果倒推法

通常，人们在分析问题的时候总是采用反向推导的方法，即从问题应该得出的结果入手，再推导出求解问题的方法。形式地说：

在认为已经求得问题结果的假定下，推导出求得问题结果所需要满足的条件，以及在此条件控制下的可执行的操作和待求解的下级问题。分层逐级进行这样的推导，直至所得结果就是问题的解。

称问题求解的这种方法为结果倒推法。仔细分析就可以看出，这个结论中含有两层意义。通过对当前问题的结果倒推，首先获得了当前需要满足的条件和可执行的操作；同时显露出了待求解的下级问题。将待求解的下级问题作为当前问题，再进行结果倒推，分层逐级进行，最终总能求得原问题的解。可以用如下的算法来表述结果倒推法：

1) 将要被求解的问题作为当前问题。

2) 对于当前问题，先假定已经求得其结果，分析得出需要满足的条件，以及在此条件控制下的可执行的操作和待求解的下级问题。

3) 如果可执行操作所得结果就是问题的解，则原问题求解结束。否则，将待求解的下级问题作为当前问题，返回步骤(2)。

 

                 

 

图5.1 结果倒推法的框图

图5.1是表示结果倒推法的框图。按这个框图人工求解问题是可以的，但无法将其编写成计算机程序，因为这只是求解问题的通用方法。在结果倒推法中，以“可执行操作所得出的结果就是问题的解”作为原问题求解结束的条件，这当然是合情合理的。既然问题求解已结束，当然也就没有“待求解的下级问题”。换句话说，没有“待求解的下级问题”等价于“可执行操作所得出的结果就是问题的解”，没有“待求解的下级问题”也是原问题求解结束的条件。这样，我们就可以用图5.2来表示结果倒推法。

原问题求解结束

还有待求解的下级问题吗？

将待求解的下级问题作为当前问题

Y

N

将原问题作为当前问题

结果倒推获得“需要满足的条件”和“可执行的操作”

 

                

 

  

图5.2 以“没有待求解的下级问题”作为原问题求解结束条件的结果倒推法框图

结果倒推法是具公理性的问题求解方法，是人们求解问题的通用方法，适用于任何问题的求解。我们将会看到，作业树的设计正是采用了这种方法。显然，采用结果倒推法编写出的程序自然贯彻了结果倒推的方法，运行相应程序也就相当于采用了结果倒推法求解问题。

需要满足的条件

结果倒推当前问题

上级控制下的可执行操作

Ct

结束语句

结果倒推法编程的

可执行操作

待求解的下级Sq

 

                  

 

 

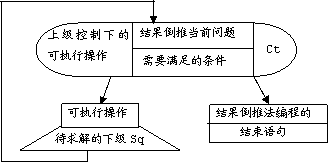
      图5.3 用结果倒推法编程的框图

对于具体问题，我们更关心的是每一次结果倒推所获得的“需要满足的条件”的具体表示。至于是否还有“待求解的下级问题”并不重要，有就继续进行结果倒推，没有就结束求解，这是顺理成章的事。所以，我们只需要连续不断地完成每一次的结果倒推，最终总会出现只有“可执行的操作”没有“待求解的下级问题”的情形。现在，我们将“可执行的操作”和“待求解的下级问题”合并成一框” ，这样做并没有改变结果倒推法的原意。一方面，它们都是在“需要满足的条件” 的控制下；另一方面，可执行的操作是已知的，下级问题是待求解的，它们形式上的合并并不会混淆实质上的分离。如此就形成了图5.3的框图，称为用结果倒推法编程的框图，其各部分的意义如下。

1) 上部端园框为“结果倒推”框，借用了作业树控制节点的表示形式。其中：注释指明本框的功能是“结果倒推当前问题”；“上级控制下的可执行操作”是从当前问题分离出来的，但它并不受本框“需要满足的条件”的控制，而是受上一级“需要满足的条件”的控制；“需要满足的条件”是对当前问题结果倒推产生的，“Ct”即为其控制类型。显然，按照前面对作业树控制节点的定义，这一框的内容可以被编写成程序。

2) 左部梯形框为“下级问题”框。它含有对当前问题结果倒推所产生的“可执行操作”和“下级问题”。即本框的这两项内容和上部框中的“需要满足的条件”，都是对当前问题结果倒推所产生的。根据结果倒推法，本框的这两项内容应受控于“需要满足的条件”，编写出的程序也同样满足这个原则。由此也可以看出，上部框中的“上级控下的可执行操作”与本框的“可执行操作”是不同的。前者是属于当前问题之前的父问题的，后者则是属于当前问题的。

3) 右部矩形框为“结束语句”框。可以想象，在连续进行结果倒推的过程中，最终总会出现没有“待求解的下级问题”的情况，意味着原问题的求解已经结束，应该编写“结束语句”作为结果倒推法程序的出口。

将图5.2与图5.3比较就可看出，虽然形式上有些差异，但它们实质意义是相同的，都是采用结果倒推法求解问题。它们之间的主要差异是图5.3中没有“还有待求解的下级问题吗？”询问框，相应功能的实现已经在上面的第3点中做了说明。此外，图5.3中省去了“将原问题作为当前问题”，是为了显目地看出结果倒推法编程的主要功能框。再说人工采用结果倒推法编程自然是从原问题开始，省去这一框并不会产生歧义。剩下其它各部分的意义都是相同的，区别仅在于“直接求解问题”和“编程求解问题”。

 

5.2 作业子树与问题

为了探讨作业树的设计原理，就必须把作业树同所求解的问题相关联，进而说明结果倒推法在作业树设计中的应用。为此，我们先要定义几个重要概念：源问题、原问题和真问题，这些概念都直接与相应作业子树相对应。然后，有针对性地规范出真问题型态树，它将是我们研究的主要作业子树。

 

5.2.1 作业子树的物理意义

(1) 源问题。

凡可以求解出结果的问题都称为源问题，缩写为Sq(Sourse question)。我们是运用作业树来求解问题的，凡被求解的问题都要将其求解算法设计成作业子树。这里说是作业子树，即不仅仅是完整的作业树，还包括采用结果倒推法设计作业树的过程中的所有作业子树。换句话说，任一棵作业子树都求解一个Sq。所以说，可以求解出结果的待求解问题都是Sq，按问题求解算法设计出的作业树所求解的问题也是Sq。

(2) 原问题。

作业树所求解的Sq称为原问题，缩写为Oq(Original question)。显然，在作业树的范围内，Oq是最大范畴的Sq。

(3) 真问题。

作业节点及其左子树所组成的作业子树所求解的问题称为真问题，缩写为Tq(True question)。这里Tq的定义中没有涉及控制节点的右子树和中子树，因为它们都不参与Tq的求解，这在后面的讨论中会有论述。显然，作业树中任何节点都是相应Sq的根节点，同时也是Tq的根节点，剪去Sq的右子树和中子树后就得到了同根的Tq。

这里将Oq、Sq和Tq都以作业子树来定义，并非多此一举。将作业子树同所求解的问题相关联，使得其物理意义更明确。后面将会看到，Oq、Sq和Tq的定义，对于揭示作业树的设计原理至关重要。为了叙述的方便，我们经常会直接以Oq、Sq或Tq来代表相应的作业子树，并将相应作业子树的根节点说成是它们的根节点，这应该不会被误会。

 

5.2.2 作业树的初始型态树

根据作业树的定义，作业树的延伸设计是从起始节点开始的，我们将在博文《冒泡排序程序的结构化设计》中定义的图1.6的作业树初始型态树重画于图5.4。

fds

起始节点

$

结束节点

return

可执行操作

待求解的下级Sq

 

 

图5.4 作业树的初始型态树

如前所述，作业树初始型态树由三部分组成：起始节点、问题求解子树和结束节点。初始型态树的结构十分简单，但却体现了结果倒推法用于作业树设计。与图1.6相比略有不同，图5.4中将左支的“受控程序段”分为“可执行操作”和“待求解的下级Sq”两部分。这里，“可执行操作”就是对Oq结果倒推所产生的已知的操作。

确立初始型态树是设计作业树的第一步，这一步设计出了作业树的起始节点和结束节点，以及在起始节点控制下的可执行操作。待求解的下级Sq中的所有节点则有待于下一步的设计。那么，我们是依据什么设计出起始节点和结束节点的呢？就是结果倒推法。

作业树初始型态树的设计原理是：在假定可以求得Oq结果的前提下，确立作业树的起始节点和结束节点，以及在起始节点控制下的可执行操作和待求解的下级Sq。

显然，上述结论是结果倒推法用于设计作业树的第一步。所谓“确立起始节点和结束节点”，实际就是画出初始型态树，这是公式化的简单设计。但“在假定可以求得Oq结果的前提下”却隐含了结果倒推法的意义，其是构造初始型态树这一步所要满足的条件。仅当认为问题是可解的，才有必要去设计作业树，确立作业树的起始节点；仅当认为问题求解是可行的，才能导出可执行操作和下级Sq；仅当认为可以求得问题的结果，才能确定运行完起始节点的左子树后就可结束作业树的运行，确立起始节点的右儿子为结束节点。

设计作业树也就是设计求解问题的程序，所以图5.4与图5.3的形状几乎完全相同。由于只是设计作业树的第一步，故而图5.4中没有循环返回线。图5.4中的“结束语句”框是针对Oq的，因为设计作业树的第一步是认为Oq的结果己经求出，当然就有求解程序的结束语句。图5.3的Oq是：用结果倒推法编写问题求解程序，对于这个Oq设计作业树的第一步，其右侧的这一框也是“用结果倒推法编写问题求解程序”的“结束语句”。只不过在前面的叙述中说成是：结果倒推法编程至没有待求解的下级问题时，才执行“结束语句”框。那里是从设计程序流程图的角度讲的，而这里是从设计作业树的角度讲的。

 

5.2.3 真问题型态树

实际上，前面定义的三类问题中最为重要的是Tq，它体现了应用结果倒推法设计作业树的本质意义。

Tq求解己结束

end

可执行操作

待求解的下级Sq

Tq的根节点

S

求解未结束

   

 

图5.5 Tq型态树

按照Tq的定义可以画出其型态树，如图5.5所示。可以看出，Tq型态树与初始型态树的形状是一样的，或者说初始型态树是以起始节点为根的Tq型态树。图5.5中Tq根节点虚拟的右儿子中也只有一条“end”语句，虚拟表示“Tq求解己结束”。根据作业树的运行规则，Tq运行结束将退回至其父节点，并不会进入其根节点的右子树。由此可见，Tq的求解实际与Sq根节点的右子树无关，所以虚拟的“求解己结束”本质上是真实的。根节点没有右子树正是Tq的突出特点。Tq根节点的控制类型要根据实际问题来确定，故而图5.5中没有给定控制类型。控制类型为“$”的Tq的型态树就是初始型态树，Oq也是范畴最大的Tq。仿照初始型态树的设计原理，我们也可以归纳出如下结论。

Tq型态树的设计原理是：在假定可以求得当前Sq结果的前提下，依据算法归纳出Sq求解结束时的状态条件和可执行操作，状态条件即是当前Tq根节点的控制逻辑表达式和控制类型，可执行操作则是下级Tq根节点顺序部中的语句，剩余待求解部分则是当前Tq根节点的Sq。

可以看出，Tq型态树的设计原理也是结果倒推法。将其与初始型态树的设计原理对照后就可以看出，它们是同一个原理的不同表述，Tq型态树的设计原理涵盖了初始型态树的设计原理。由初始型态树的设计原理可知，起始节点是对Oq采用结果倒推法得出的。换句话说，范畴最大的Sq并不是初始型态树中的问题求解子树，而是Oq自身。尽管Oq形式上并不是作业树中某节点的左子树，它就是作业树自身，但它的确是Oq的问题求解树。初始型态树只不过是Oq的Tq型态树，采用Tq型态树的设计原理作用于Oq就可以构建出初始型态树。Tq型态树的设计原理中有如下隐含意义：

1) Tq根节点的控制逻辑表达式恒为“求解未结束”。

我们注意到，图5.5中Tq根节点的控制逻辑表达式固定为“求解未结束”，即将其认为是“Sq求解结束时的状态条件”。由于Tq的根节点只有左子树，运行完该左子树后就求得了Tq的解，即“Tq求解己结束”。所以，Tq根节点的控制逻辑表达式必定是“求解未结束”，才能使控制既可以前进求解问题，又可以后退结束运行。当然，“求解未结束”只是从普遍意义上对控制逻辑表达式的通俗表述，根据算法得出的逻辑表达式必定具有“求解未结束”的意义。譬如起始节点中的函数定义语句就具有“求解未结束”的意义，致使控制进入它后就被强令向左运行它的左子树。

2) Tq根节点中的顺序段是由上级Tq型态树的设计而得出的。

在结果倒推法中，有“逐级推导出所需满足的条件和可执行的操作”的叙述。其中“所需满足的条件”就是“求解未结束”，而“可执行的操作”则对应于Tq根节点顺序部中的顺序段S。值得注意的是，当前的顺序段S并不是因归纳得出当前Tq的根节点而产生的，而是在设计出上级Tq型态树后就已经得出了，故它是受上级Tq的根节点控制的。

3) Tq虚拟结束节点的意义。

在图5.5的Tq型态树中，画有以虚线表示的Tq的结束节点，是为了说明Tq的运行情况与初始型态树类似。根据作业树运行规则，Tq运行结束后控制将退向其父节点，这相当于执行了Tq虚拟右子树中的结束语句。作业树中任何Tq的运行都会结束，且最终都会退至起始节点，进而运行真实的结束节点。所以，虚拟结束节点是真实结束节点在Tq型态树中的影像，最终的确具有结束运行的意义。由Tq的定义可知，Tq根节点的右子树不属于Tq，但这并不意味着Tq的根节点一定没有右子树。当控制类型为“？？”时，其当然会连接有右子树。在后面的叙述中将会说明控制节点右子树的物理意义。

 

5.3 问题递归处理

实际上，Tq型态树是图5.3中每一次循环结果倒推的图形表示，将这些Tq逻辑地连接就会形成作业树。也可以说，Tq型态树的设计原理只用了结果倒推法的前半部分：在认为已经求得问题结果的假定下，推导出求得问题结果所需要满足的条件，以及在此条件控制下的可执行的操作和待求解的下级问题。结果倒推法还有后半部分：分层逐级进行这样的推导，直至所得出的结果就是问题的解(没有待求解的下级问题)。所谓“待求解的下级问题”，就是前面定义的Sq。对逐级出现的Sq都设计出相应的Tq型态树，就可完成作业树的设计。

自Oq开始，逐级递归地设计出Sq的Tq型态树，直至所有通路上的最后一级Sq中都不含控制，就完成了作业树的设计。

上述结论称为问题递归处理，本质上就是对Sq的递归设计。由图5.5可以看出，去掉Tq的根节点后就露出了下级Sq，再设计出该Sq的Tq型态树，…，如此连续处理就是对Sq的“逐级递归设计”。问题递归处理中的所谓“不含控制”，就是结果倒推法中的“没有待求解的下级问题”。作业树中会有许多通路，每条通路上最后总会出现不含控制的Sq，也就是作业树的叶节点。所有通路上的Sq递归设计都抵达叶节点，作业树的设计自然就完成了。

问题递归处理是结果倒推法用于作业树设计的表述形式，本质上它们是同一个原理。结果倒推法是人们公认的问题求解方法，问题递归处理自然也是公理。当然，后面还是会证明问题递归处理的通用性。接下来我们将要运用问题递归处理，进一步分析控制作业的控制类型和顺序段的确立。

(1) Tq的求解完全由其根节点左口的Sq承担

由Tq型态树可以看出，每个控制节点能且只能对应于一个Tq，控制节点是Tq的根节点。另一方面，Tq根节点的逻辑表达式的普遍意义恒为“求解未结束”，只有当其值为“真”时才能向前继续求解。如果节点的控制类型为“！”或“？”，则只有左口可以连接下级Sq，这两类控制下的继续求解都只能是Tq左口的Sq。如果节点的控制类型为“？？”，虽然其右口也接有子树，但右子树与以当前控制节点为根的Tq的求解无关。因为只有当“求解未结束”为“假”时控制才会进入右子树，即并未求解以当前控制节点为根的Tq，而是转入了以当前控制节点的右儿子为根的Sq的求解。

由上面的叙述就可以得出结论：Tq的求解完全由其根节点左口的Sq承担。实际上，任何含有控制的Sq都是由若干级Tq组成的，完成了其所有Tq的求解，也就完成了Sq的求解。完成了作业树中所有Tq的求解，也就完成了Oq的求解，这同我们在前面得出的结论是一致的。任何控制节点的左口都是非空的，因为它要求解相应的Tq。

如果单次运行控制节点左口的Sq就可以结束以该控制节点为根的Tq的求解，则采用条件控制，否则采用循环控制。

根据上述结论，我们就可以决定控制作业的控制类型是条件控制还是循环控制。至于是单向条件控制还是双方条件控制，下面的叙述将会给出答案。

(2) 起始节点的左儿子是Oq问题递归处理的起点

我们知道，作业树的根节点即为起始节点，其只有一条函数定义语句，没有可执行语句，所以它并没有参与Oq的求解。另一方面，起始节点的右子树中只有一条结束语句，也没有问题求解功能。所以，起始节点的左子树承担了求解Oq的全部功能，该左子树是实质上的Oq，换句话说：

起始节点的左儿子是Oq问题递归处理的起点，“Oq求解已结束”的状态条件的逻辑非就是起始节点左儿子的控制逻辑表达式。

有了上述结论，我们就可以从推导“Oq求解已结束”的状态条件开始，问题递归地设计作业树。

(3) 一个Sq可能对应于多个Tq

如上所述，一个控制节点能且只能对应于一个Tq，或者说每个Tq有且只能有一个控制节点作为根节点。现在来考察用结果倒推法处理Sq的情况。考察的结果是：一个Sq可能归纳出多个控制作业，对应于多个Tq；也可能不含控制，对应于顺序作业。

由于Sq是待设计成作业子树的程序段，问题递归即是对Sq的分级处理。所以，对于某一级的Sq，结果倒推法只是归纳出其当前的控制作业。逐级归纳出Sq的当前控制作业，就实现了问题递归处理。如前所述，作为Tq根节点的控制节点，其逻辑表达式的普遍意义恒为“求解未结束”。然而，在进行结果倒推法处理时，有的Sq可能会有多个当前的“求解已结束”，这意味着可以同时形成多个“求解未结束”的控制节点，即这样的Sq对应着多个Tq。譬如“解一元二次方程”问题，它有三种类型的解：两个不相等的实根，两个相等的实根，两个共轭虚根。只要求出其中的一类解，就算问题求解已结束。可见这个Sq有三个“求解已结束”，亦即需要三个“求解未结束”。而作业树的每个控制节点只能处理一个“求解未结束”，三个“求解未结束”就必须要有三个控制节点，对应着三个Tq。换句话说，多个同时存在的“求解已结束”可以分为多个Tq来求解，每个Tq的根节点对应于一个控制作业。于是就有结论：

对于含有多个“求解已结束”的Sq，可以采用双向条件控制逐级分支处理。双向条件节点的右子树亦是Sq，但该Sq不属于以双向条件节点为根的Tq。

上述结论的前半部分很好理解，每个条件控制节点都与它的左子树组成一个Tq，多个条件控制节点就可以求解多个Tq。所有这些Tq都是为求解Sq服务的，必须逻辑地将它们组合在同一棵作业树中。所以就必须采用双向条件控制，左口求解各自的Tq，右口则用来组合这些Tq，这就是结论后半部分的意思。前面有过结论，Tq的求解完全由其左口的Sq承担，即右口的Sq不属于以双向条件节点为根的Tq。如果控制进入双向条件节点时“求解未结束”为假，控制将进入双向条件节点的右口，这意味着不选择求解以当前双向条件节点为根的Tq，而选择运行其右口的Sq。

(4) 中口程序段不参与Sq的求解，只对Sq的求解结果做非加工性安排

我们定义过，每个控制节点可以有三个向下延伸的接口，其中左口和右口连接的程序段的功能己经有了结论，剩下中口程序段的功能还没有讨论。

根据定义，中口程序段不受该中口所在控制节点的控制，却要在该控制节点运行之后紧接着无条件地被运行。这说明，中口程序段不参Sq的求解，因为控制节点运行结束就意味着其所对应的Sq的求解已结束。在求得Sq的结果之后再运行中口程序段，可见中口段程序只能是对Sq的结果做非加工性安排。所谓非加工性安排，无非是存贮、传送或输出等非加工性的操作，决不会改变求解结果。所以说，中口程序段虽然属于Sq，但它却不参与Sq的求解，其功能仅仅是对Sq的结果做非加工性处理。

(5) 顺序作业是不含控制的Sq

前面提到，Sq可能归纳出多个控制作业，它也可能不含控制。当问题递归处理至不含控制的Sq时，意味着作业树的相应通路上的控制节点都已设计完成，这个不含控制的顺序作业即为叶节点。换句话说，顺序作业是作业树中控制通路上问题递归的终点，只要执行完顺序作业中的操作，这条通路上的问题求解就算结束了。所有通路上的问题递归处理都抵达了顺序作业，Oq的作业树设计也就完成了。

实际上，将顺序作业说成是不含控制的Sq并不准确，但却能方便叙述。由作业树控制节点的定义可知，其顺序段是受上级节点控制的，与自身的控制无关。当作业节点不含控制时，就意味着没有待求解的下级问题，或说没有下级Sq。由此可见，顺序作业与这个“不存在的下级Sq”毫无关系，自身更谈不上是Sq。将顺序作业中的顺序段假想成与这个不存在的Sq组合，就认为顺序作业是不含控制的Sq，或说是没有待求解的下级问题的Sq。

(6) 控制节点接口功能

从上面的叙述可以看出，控制节点的三个接口都有各自特定的功能，现在我们来归纳它们。

1) 左口的功能是连接求解Tq的Sq。

这一条在前面已经有过充分的论述。Oq的求解是通过问题递归地求解Tq来实现的，而Tq的求解是由左口的Sq完成的，所以任何控制节点的左口都是非空的。控制节点左口的控制类型为“？”或“！”。

2) 右口的功能是分支并列的Tq。

所谓并列的Tq，即为求解同一个Sq而同时存在的互不相关的Tq。这些Tq的处理是没有先后顺序的，作业树中以控制节点的右口来分支连接直接属于同一个Sq的Tq。所以，控制节点右口的控制类型恒为“？”，当然也可以为空。

3) 中口的功能是连接非加工性的Sq。

控制节点中口所连接的Sq是不受控的，不参与其父节点Sq的求解，仅仅对父节点Sq的结果做非加工性的安排。控制节点中口的控制类型恒为“*”，当然也可以为空。

 

5.4 问题递归实例分析

由上面的叙述我们知道，问题递归处理就是作业树的设计原理，而问题递归处理又是结果倒推法用于作业树设计的形式表述，作业树的设计原理本质上是结果倒推法。现在结合实例来看一看问题递归处理的应用，这些实例都贴出过单独的博文。

5.4.1 冒泡排序问题

这里，我们将博文《冒泡排序程序的结构化设计》中的图1.7拷贝于图5.6。冒泡排序作业树中有三个控制节点，其中两个是循环控制，一个是单向条件控制。为了叙述的方便，今后对于己经确立了根节点X的Sq，就直接称之为X问题。

i＜n

!w*

S1

k＜n

!w*

S2

a(k)<x

?

S3

S4:x换成小的

w=x; x=a(k); a(k)=w;

S5:安排小的

a(i)=x;

stop

S6:A的元素已排序

printf A

bubsort()

$

node0

node1

node2

node3

S7:结束

S1：输入A的元素，i=0,n=10； S2：i=i+1；k=i；x=a(k)； S3：k=k+1；

  

 图5.6 冒泡排序的作业树

1) node1是起始节点的左儿，所以node1问题就是Oq，即“将A的n个元素排序”。该问题“求解已结束”的状态是：A中的n个元素已经从小到大排好序。根据冒泡排序算法，指针i从1逐步增值至n的过程，都属于“求解未结束”。一旦有i=n，说明A的元素已全部排好序，问题求解已经结束，“求解已结束”的状态条件是i≥n。所以，node1的逻辑表达式是i＜n，控制类型为“!”。

2) node2问题是node1的下级Sq。这个问题是要求在未排序部分a(i)至a(n)段中找出最小元素，即“在无序集中找出最小元素”。依据算法，指针k从i+1逐步增值至n的全过程都属于“求解未结束”。一旦有k=n，说明最小元素已经找到。所以，node2的逻辑表达式为“k＜n”，控制类型为“!”。

3) node3问题是node2的下级Sq。这个问题是要求将x同a(k)进行比较，即“比较两元素的大小”。依据算法，仅当a(k)小于x时才属“求解未结束”，以便运行node3的左子树。所以，node3的逻辑表达式为“a(k)<x”。两个元素只需比较一次就可得出结果，故node3的控制类型为“?”。

4) node3的下级Sq是“交换两存储单元的内容”。显然，这个问题中没有控制，直接执行相应的顺序语句就可以了。同时说明，问题递归在这一条控制通路上已经到达终点，本Sq就是作业树的一个叶节点。

5) 相关控制结。本例中有两个控制结，分别对应于node1和node2的中口。可以看出，这两个中口所连接的程序语句都没有对相应问题的结果数据再加工，仅仅做了打印输出和更换存储单元。

 

5.4.2 解一元二次方程问题

在上例中考察过含有循环控制和单向条件控制的问题递归处理，现在来看含有双向条件控制的问题递归处理的实例。这个例子在博文《解一元二次程程序的结构化设计》中有过详细的叙述，这里将该文中的图2.1拷贝于图5.7中。

S5:打印输出

printf x1,x2

Quad()

$

C0：起始作业

S2:计算不等实根

=(-b+ )/2a =(-b- )/2a

δ>0

??

C1

S1:输入a,b,c； δ=b2-4ac；

δ=0

??

C2

S4:计算两个虚根

δ=-δ; y= /2a =-b/2a+iy =-b/2a-iy

S3:计算相等实根

=-b/2a =

return

S6:结束作业

S1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

图5.7 解一元二次方程的作业树

我们知道，一元二次方程“ax²+bx+c=0”有三种解：两个不相等的实根，两个相等的实根，两个共轭虚

 

根，这三种解是互斥的，能且只能求得一种解，只要求出其中的一种解，问题求解就算结束。由此可见，这个Sq有三个并列的“求解已结束”，我们将该问题分为三个Tq来求解，使之各自对应于一个根节点。如前所述，这类问题必须采用双向条件分支控制，以便将三个Tq分别逐个求解，现在来看图5.7中的问题递归情况。

1) 问题递归的第一步可以选择当前Sq的三个Tq中的任何一个，这里选择“求两个不相等实根”作为当前Tq，C1为其根节点。显然，只有当“δ>0”为“真”时C1问题才能继续求解，故C1的逻辑表达式为“δ>0”，控制类型为“？？”。

2) 问题递归的第二步是在第一步的基础上进行的，这里选择当前Sq剩下的两个Tq中的“求两个相等实根”作为当前Tq，C2为其根节点，其也是C1的右儿子。对于C2问题，只有当“δ=0”为“真”时才能继续求解，“δ=0”就是C2的逻辑表达式，控制类型为“？？”。

3) 问题递归的第三步只剩下“求两个共轭虚根”作为当前Tq，其“求解未结束”逻辑表达式为“δ<0”。由于此前的问题已经判断过“δ>0且δ=0”为“假”，剩下的只有“δ<0”为“真”了，这正是当前Tq继续求解的条件。所以，可以缺省以“δ<0”为逻辑表示式的单向条件控制，直接将本Sq作为C2的右儿子即可被求解。

4) 控制结。这里将“打印输出”处理置于C1的中口，就可以打印出任何一种类型的解。

 

5.4.3 二分查找问题

在冒泡排序作业树中只有循环和单向条件控，没有双向条件控制；而在解一元二次方程的作业树中只有双向条件控制，没有循环控制。现在我们来分析二分查找问题，其作业树中既有循环控制又有双向条件控制。该问题在博文《常用二分查找程序的作业树》中有详细叙述，现将其中的图3.1拷贝于图5.8中。

 

Bsearch ()

$

C0：起始作业

L1:指针g左移

g=i-1

S1: 输入x；m=“n”; f=1，g=100； S2：i=((f+g)/2)的整数部分

return (m,i)

L4:结束作业

!w

C1

S1

f≤g且m=“n”

??

C2

S2

x<v（i）

??

C3

x>v（i）

L2:指针f右移

f=i+1

L3:必有x=v（i）

m=“y”

图5.8 常用二分查找的作业树

1) C1问题即是Oq：在有序元素序列中二分查找x。该问题“求解已结束”的状态条件有两个：成功找到则有x=v(i)后置m=“y”；或x不在序列中查找失败，就有f>g。这两个条件合并在一起的逻辑表达式为：(f>g或m=“y”)，表示node1问题“求解已结束”。将其求反后为：(f≤g且m=“n”)，即为C1的控制逻辑表达式，控制类型为“！*”。

接下来，以C1为根的Tq的左子树对应的Sq为：确定x的查找范围。这个问题的“求解己结束”情况与“解一元二次方程”的问题类似，它也同时面临3个Tq，对应于3个控制逻辑表达式：x＜v(i)；x＞v(i)；x=v(i)。只要执行过其中一个Tq，就算完成了这个Sq的一次“求解已结束”。所以必须用双向条件控制来分支安排它们，如下所述。

2) 第1个Tq是C2问题：如果x＜v(i)则令g=i-1，继续在v(f)和v(g)之间查找。

3) 第2个Tq是C3问题：如果x＞v(i)则令f=i+1，继续在v(f)和v(g)之间查找。

4) 第3个Tq是：如果x=v(i)则置m=“y”，将其直接作为C3的右子树。

其中节点C1是循环控制，控制退至该节点时，只要满足循环条件，控制又会再次向前，以便确定下一次的查找范围。在循环控制的作用下，C2的 Tq和C3 的Tq都有机会被运行。C3右口的子树实际是缺省了以“x=v(i)?”作为根节点的Sq的左子树，同样有机会被运行。我们称循环控制的这种功能为运行反射，它使得循环体内的每一条通路都有机会被运行。

 

顺便指出，在工程应用中设计作业树时，并不需要象对上述的三个例子那样进行问题递归分析。只要设计出了算法，作业树的设计是一件极具规律而又富于创意的事情。

 

5.6 结束语

大凡一门学科都有她的原理，有机械设计原理，电工原理，化工原理，无线电原理，…。这些原理也都不是几句话能说清楚的，而是一本厚厚的书。书中叙述的都是对相应学科客观规律的归纳与总结，然后上升到理论的高度，用数理化的基本定理加以推导和证明，就形成了原理。本文认为，按结果倒推法问题递归地表示算法，就是作业树的设计原理。那么，结果倒推法又是依据什么呢？我回答不出来。或者可以这样回答：结果倒推法是人们在解决问题时通用的思维方法。最为典型的是对平面几何问题的证明，中学老师总是教我先从认可问题的结论成立入手，然后逐步推导出需要满足的条件，包括如何添加辅助线，如何运用基本定理。直至推导到题目中己经给出的己知条件，然后再从己知条件开始书写证明过程。实际上，结果倒推法不仅仅用于数学证明，而是在人们的日常生活中普遍地被采用。计算机软件是对客观规律的模拟，她将人们求解问题的思维结果以形式语言方式告诉计算机。作业树是表示算法的工具，算法则是人们为求解问题而总结出的解题方法。所以说，用结果倒推法设计作业树只不过体现了人们求解问题的思维活动，加以归纳总结后就认为是原理。

作业树的产生当然不会是凭空而来的，在下一篇博文《作业树的通用性证明》中将会有所叙述，人们对作业树的设计原理也将会有进一步的认识。