RMQ(Range Minimum Query)
问题
RMQ问题是求给定区间中的最值问题。对于长度为n的数列A,回答若干查询RMQ(A, i, j)。返回数组A中下标在[i,j]里的最小值的下标。比如数列 5,8,1,3,6,4,9,5,7 那么RMQ(2,4) = 3, RMQ(6,9) = 6.
解决方法
主要方法及复杂度(处理复杂度和查询复杂度)如下:
朴素(即搜索) O(n)-O(n)
ST(实质是动态规划) O(nlogn)-O(1)
线段树(segment tree) O(n)-O(qlogn)
朴素
即是直接搜索,对被查询的空间进行直接遍历,时间复杂度为O(n)
ST
Sparse Table,它是一种动态规划的方法。
以最小值为例。a为所寻找的数组. 用一个二维数组f(i,j)记录区间[i,i+2^j-1](持续2^j个)区间中的最小值。其中f[i,0] = a[i]; 所以,对于任意的一组(i,j),f(i,j) = min{f(i,j-1),f(i+2^(j-1),j-1)}来使用动态规划计算出来。 这个算法的高明之处不是在于这个动态规划的建立,而是它的查询:它的查询效率是O(1).
假设我们要求区间[m,n]中a的最小值,找到一个数k使得2^k<n-m+1. 这样,可以把这个区间分成两个部分:[m,m+2^k-1]和[n-2^k+1,n].我们发现,这两个区间是已经初始化好的.
前面的区间是f(m,k),后面的区间是f(n-2^k+1,k).
这样,只要看这两个区间的最小值,就可以知道整个区间的最小值!
伪代码:
//初始化 INIT_RMQ //max[i][j]中存的是从i开始的2^j个数据中的最大值,最小值类似,num中存有数组的值 for i : 1 to n max[i][0] = num[i] for j : 1 to log(n)/log(2) for i : 1 to (n+1-2^i) max[i][j] = MAX(max[i][j-1], max[i+2^(j-1)][j-1]) //查询 RMQ(i, j) k = log(j-i+1) / log(2) return MAX(max[i][k], max[j-2^k+1][k])
C++模板:
/**
* @brief sparse algorithm
* @author xiyan
* @date 2014/6/17
* @last edit
*
*/
#include <cstdlib>
#include <iostream>
#include <cmath>
typedef unsigned int size_t;
typedef int ssize_t;
namespace rmq{
using namespace std;
template<typename T>
class sparseTable{
public:
ssize_t createSt(const T *arrayPtr, const ssize_t arraySize);
/*build st by input*/
const T *searchSt(const ssize_t startPos, const ssize_t endPos);
/*lookup the min val from startPos to endPos*/
virtual ~sparseTable(void);
/*destory st when class destory*/
virtual void debug(void);
private:
ssize_t allocSt(const ssize_t arraySize); /*alloc space for st*/
ssize_t initSt (const T *arrayPtr); /*init St*/
ssize_t stLog(ssize_t size) const; /*make lg(size)*/
T * getItem(const ssize_t base, const ssize_t logTots); /*get item from sparse table*/
void destorySt(void);
ssize_t *getMaxLogTots(void){
return &tot_row;
}
ssize_t *getMaxBase(void){
return &tot_col;
}
T *dpSt; /*sparse table*/
ssize_t tot_row; /*sparee table tot row*/
ssize_t tot_col; /*sparse table tot col */
};
/**
* @brief deinit api for st
* @note call destorySt to do clean task
*/
template<typename T>
void sparseTable<T>::debug(void){
cout << "tot nums(lg):"<< *getMaxLogTots() << endl;
cout << "tot base :"<< *getMaxBase() << endl;
if(dpSt){
for(ssize_t tot = 0; tot < *getMaxLogTots(); tot++)
for(ssize_t base = 0; base < *getMaxBase(); base++){
cout << "Logtot " << tot;
cout << ",";
cout << "base " << base;
cout << "| ->";
cout << *getItem(base, tot) << endl;
}
}
}
/**
* @brief deinit api for st
* @note call destorySt to do clean task
*/
template<typename T>
void sparseTable<T>::destorySt(void){
delete dpSt;
}
/**
* @brief play as a cleaner when destory st
*
*/
template<typename T>
sparseTable<T>::~sparseTable(void){
destorySt();
}
/**
* @brief 2^n <= size, return n;
* @return n success, -1 fail
*
*/
template<typename T>
ssize_t sparseTable<T>::stLog(const ssize_t size) const {
ssize_t ans = 0;
if(size <= 0){
return -1;
}
while( (1 << ans) <= size){
++ans;
}
ans--;
return ans;
}
/**
* @brief create sparse Table
* @param[in] arrayPtr base data store in array for building sparse table
* @param[in] data tots
* @return 0 success, -1 fail
*/
template<typename T>
ssize_t sparseTable<T>::allocSt(const ssize_t arraySize){
ssize_t *maxBase = getMaxBase();
ssize_t *maxLogTots = getMaxLogTots();
*maxBase = arraySize;
*maxLogTots = stLog(arraySize);
if( *maxLogTots < 0){
return -1;
}
*maxLogTots += 1;
ssize_t totSize = (*maxBase) * (*maxLogTots);
dpSt = new T[totSize];
if(NULL == dpSt){
return -1;
}
return 0;
}
/**
* @brief get Item from table
* @note
* 1. row act as totnums cnt
* 2. col act as idx for base num
* 3. col >= row for Table
*/
template<typename T>
T *sparseTable<T>::getItem(const ssize_t base, const ssize_t logTots){
if( !dpSt || base < 0 || logTots < 0 || base >= *getMaxBase() || logTots >= *getMaxLogTots()){
return NULL;
}
return (&dpSt[logTots * (*getMaxBase()) + base]);
}
/**
* @brief init sparse Table by input
* @param[in] arrayPtr ptr to the imput array
*/
template<typename T>
ssize_t sparseTable<T>::initSt(const T *arrayPtr){
for(ssize_t base = 0; base < *getMaxBase(); base++){
T * itemPtr = getItem(base, 0);
if(NULL == itemPtr){
return -1;
}
*itemPtr = arrayPtr[base];
}
#if 0
cout << "init phase0 success" << endl;
#endif
for(ssize_t logTots = 1; logTots < *getMaxLogTots(); logTots++){
for(ssize_t base = 0; ((base + (1 << logTots) ) <= (*getMaxBase())); base++){
T *lItem = getItem(base, logTots - 1);
T *rItem = getItem(base + (1 << (logTots - 1)), logTots - 1);
T *cItem = getItem(base, logTots);
if(NULL == lItem || NULL == rItem|| NULL == cItem){
return -1;
}
*cItem = (*lItem < *rItem ? *lItem : *rItem);
}
}
#if 0
cout << "init phase1 success" << endl;
#endif
return 0;
}
/**
* @brief create and init sparse table
* @param[in] arrayPtr ptr to the input array
* @param[in] arrSize tot nums of input
*
*/
template<typename T>
ssize_t sparseTable<T>::createSt(const T *arrayPtr, const ssize_t arraySize){
/*build st by input*/
if(allocSt(arraySize) < 0){
cout << "alloc sparse table fail" << endl;
return -1;
}
if(initSt(arrayPtr) < 0){
destorySt();
cout << "init sparse table fail" << endl;
return -1;
}
return 0;
}
/**
* @brief search the min num
* @param[in] arrayPtr ptr to the input array
* @param[in] arrSize tot nums of input
*
*/
template<typename T>
const T * sparseTable<T>::searchSt(const ssize_t startPos, ssize_t endPos){
ssize_t logPos;
if(startPos < 0 || endPos < 0|| startPos >= *getMaxBase() || endPos >= *getMaxBase()|| startPos > endPos){
return NULL;
}
logPos = stLog(endPos - startPos + 1);
if(logPos < 0){
return NULL;
}
T *lItem = getItem(startPos, logPos);
T *rItem = getItem(endPos - (1 << logPos) + 1, logPos);
if(NULL == lItem || NULL == rItem){
return NULL;
}
return (*lItem < *rItem ? lItem : rItem);
}
}//?end of sparse table?
线段树
线段树能在对数时间内在数组区间上进行更新与查询。 定义线段树在区间[i, j] 上如下:
第一个节点维护着区间 [i, j] 的信息。
if i<j , 那么左孩子维护着区间[i, (i+j)/2] 的信息,右孩子维护着区间[(i+j)/2+1, j] 的信息。
可知 N 个元素的线段树的高度 为 [logN] + 1(只有根节点的树高度为0) .
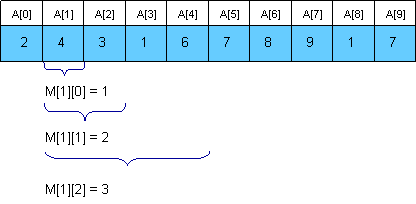
下面是区间 [0, 9] 的一个线段树:
线段树和堆有一样的结构, 因此如果一个节点编号为 x ,那么左孩子编号为2*x 右孩子编号为2*x+1.
使用线段树解决RMQ问题,关键维护一个数组M[num],num=2^(线段树高度+1).
M[i]:维护着被分配给该节点(编号:i 线段树根节点编号:1)的区间的最小值元素的下标。 该数组初始状态为-1.
/**
* @brief segment stree
* @author xiyan
* @date 2014/6/17
* @last
*/
#include <iostream>
#include <cstdlib>
#include <cstring>
namespace rmq
{
using namespace std;
typedef unsigned int size_t;
typedef signed int ssize_t;
static ssize_t inline getLftNode(const ssize_t idx)
{
return (idx << 1);
}
static ssize_t inline getRhtNode(const ssize_t idx)
{
return ((idx << 1) + 1);
}
template<typename T>
class segmentTree
{
public:
segmentTree(void):deps(0), nodes(0), elems(0), tree(NULL) {}
ssize_t createSt(const T *input, const ssize_t cnt);
~segmentTree(void)
{
destorySt();
}
const T * searchSt(const ssize_t lftQuery, const ssize_t rhtQuery);
virtual void debug(void);
private:
ssize_t allocSt(const ssize_t cnt);
ssize_t initSt(const T *input);
ssize_t initNode(const ssize_t nodeIdx, const ssize_t lftIdx, const ssize_t rhtIdx, const T *input);
const T *searchNode(const ssize_t nodeIdx, const ssize_t lftIdx, const ssize_t rhtIdx, \
const ssize_t lftQuery, const ssize_t rhtQuery);
void destorySt(void);
ssize_t log(const ssize_t x) const;
bool checkPow(const ssize_t x) const;
T *tree;
ssize_t deps; /*dep of the tree*/
ssize_t nodes; /*nodes tots*/
ssize_t elems; /*element tots*/
};
/**
* @brief 2^n <= x, return n;
* @return n success, -1 fail
*
*/
template<typename T>
ssize_t segmentTree<T>::log(const ssize_t x) const
{
ssize_t ans = 0;
ssize_t cnt = x;
if(cnt <= 0)
{
return -1;
}
while( (1 << ans) <= cnt)
{
++ans;
}
ans--;
return ans;
}
/**
* @brief make sure the input is pow of 2
* @return n success, -1 fail
*
*/
template<typename T>
bool segmentTree<T>::checkPow(const ssize_t x) const
{
if(x <= 0)
{
return false; /*x <= 0*/
}
if(!(x & (x - 1)))
{
return true; /*x == 2^n*/
}
else
{
return false; /*x > 0 && x != 2^n*/
}
}
/**
* @brief get the dep and the size for tree
* @param[in] cnt tots of the input to build tree
*
*/
template<typename T>
ssize_t segmentTree<T>::allocSt(const ssize_t cnt)
{
if(cnt <= 0)
{
return -1;
}
ssize_t depTmp = log(cnt);
if(depTmp < 0)
{
return -1;
}
if(!checkPow(cnt))
{
depTmp++;
}
depTmp++;
ssize_t nodeTots = (1 << depTmp) - 1; /*nodes needed */
nodeTots++; /*add empty node at head*/
tree = new T[nodeTots];
if(!tree)
{
return -1;
}
memset(tree, 0, nodeTots);
deps = depTmp; /*store cnt*/
nodes = nodeTots;
elems = cnt;
return 0;
};
/**
* @brief init tree
*
*/
template<typename T>
ssize_t segmentTree<T>::initSt(const T *input)
{
const ssize_t rootNode = 1;
const ssize_t lftIdx = 0;
const ssize_t rhtIdx = elems - 1;
if(initNode(rootNode, lftIdx, rhtIdx, input) < 0)
{
return -1;
}
return 0;
}
/**
* @brief init node and continue to build children
* @param[in] nodeIdx curr node
* @param[in] lftIdx start idx for input
* @param[in] rhtIdx end idx for input
* @param[in] store for input
* @return -1 error
* 0 success
*/
template<typename T>
ssize_t segmentTree<T>::initNode(const ssize_t nodeIdx, const ssize_t lftIdx, const ssize_t rhtIdx, const T *input)
{
//cout << "nodeIdx = " << nodeIdx << "," << "nodes =" << nodes << endl;
cout << lftIdx << " "<< rhtIdx << endl;
if(nodeIdx >= nodes) /*segment error*/
{
return -1;
}
if(lftIdx == rhtIdx)
{
tree[nodeIdx] = input[lftIdx];
return 0;
}
ssize_t midIdx = (lftIdx + rhtIdx) >> 1;
ssize_t curNode = nodeIdx;
ssize_t lftNode = getLftNode(curNode);
ssize_t rhtNode = getRhtNode(curNode);
if(initNode(lftNode, lftIdx, midIdx, input) < 0)
{
return -1;
}
if(initNode(rhtNode, midIdx + 1, rhtIdx, input) < 0)
{
return -1;
}
tree[curNode] = (tree[lftNode] < tree[rhtNode] ? tree[lftNode] : tree[rhtNode]);
return 0;
}
/**
* @brief create segment tree
* @param[in] input elems used to build segment tree
* @param[in] cnt tot nums of elems
* @return 0 success, -1 fail
*/
template<typename T>
ssize_t segmentTree<T>::createSt(const T *input, const ssize_t cnt)
{
if(allocSt(cnt) < 0)
{
cout << "alloc space for segment tree fail" << endl;
return -1;
}
if(initSt(input) < 0)
{
cout << "init segment tree fail" << endl;
return -1;
}
return 0;
}
/**
* @brief search ans for the query range
* @param[in] nodeIdx node index
* @param[in] lftIdx lft index for data store
* @param[in] rhtIdx rht index for data store
* @param[in] lftQuery lft for query range
* @param[in] rhtQuery rht for query range
*/
template<typename T>
const T * segmentTree<T>::searchNode(const ssize_t nodeIdx, const ssize_t lftIdx, const ssize_t rhtIdx, \
const ssize_t lftQuery, const ssize_t rhtQuery)
{
if(lftIdx > rhtQuery || rhtIdx < lftQuery)
{
return NULL;
}
if( lftQuery <= lftIdx && rhtQuery >= rhtIdx)
{
return (&tree[nodeIdx]);
}
ssize_t midIdx = (lftIdx + rhtIdx) >> 1;
ssize_t curNode = nodeIdx;
ssize_t lftNode = getLftNode(curNode);
ssize_t rhtNode = getRhtNode(curNode);
const T *lftans = searchNode(lftNode, lftIdx, midIdx, lftQuery, rhtQuery);
const T *rhtans = searchNode(rhtNode, midIdx + 1, rhtIdx, lftQuery, rhtQuery);
if(!lftans)
{
return rhtans;
}
if(!rhtans)
{
return lftans;
}
return (*lftans < *rhtans ? lftans : rhtans);
}
template<typename T>
const T * segmentTree<T>::searchSt(const ssize_t lftQuery, const ssize_t rhtQuery)
{
if(lftQuery < 0 || rhtQuery >= elems || lftQuery > rhtQuery)
{
return NULL;
}
const T *ans;
const ssize_t rootNode = 1;
const ssize_t lftIdx = 0;
const ssize_t rhtIdx = elems - 1;
if( NULL == (ans = searchNode(rootNode, lftIdx, rhtIdx, lftQuery, rhtQuery)))
{
return NULL;
}
return ans;
}
/**
* @brief destory the array for store tree
*
*/
template<typename T>
void segmentTree<T>::destorySt(void)
{
delete tree;
deps = 0;
nodes = 0;
elems = 0;
}
/**
* @brief debug segment tree
*
*/
template<typename T>
void segmentTree<T>::debug(void)
{
cout << "deps : " << deps << endl;
cout << "nodes: " << nodes << endl;
cout << "elems: " << elems << endl;
}
}
参考文章
http://blog.csdn.net/huangxy10/article/details/7945856
http://blog.163.com/zhaohai_1988/blog/static/209510085201263011135062/