Support Vector Machines 笔记

Support Vector Machines (支持向量机)属于监督学习算法, 它通过寻找最佳分隔超平面来对训练集进行分类. 

优点	泛化错误率低, 计算开销不大, 结果易解释
缺点	对参数调节和核函数的选择敏感, 原始分类器不加修改仅适用于处理二类问题
适用数据类型	数值型, 标称型

基础概念

1. SVM 的实质
SVM 算法的核心在于最优分类超平面的确定, 即通过训练样本确定分类器函数的参数. 确定分类超平面, 实质上是求解一个二次优化的问题, 通过求解对偶问题确定分类器的参数. 

2. SVM 的目标
SVM 的目标是寻找最优分类超平面, 最优分类超平面就是要求分类边界不但能将两类正确分开(训练错误率为0),且使分类间隔最大.
SVM考虑寻找一个满足分类要求的超平面, 并且使训练集中的点距离分类面尽可能的远, 也就是寻找一个分类面使它两侧的空白区域(margin)最大.

3. Support Vector(支持向量) 
支持向量就是两类样本中离分类面最近的点. 本文的主要工作就是最大化支持向量到分隔超平面的距离. 如下图 H 是分隔超平面, H₁, H₂ 上的样本就是支持向量.

4. 拉格朗日乘子
拉格朗日乘子用于在带等式约束条件下求最优化值; 如果是不等约束, 则应使用 KTT 条件. 本文根据拉格朗日乘子得到的优化目标函数如下, 本文的主要计算就在于求解公式中的 alpha 值:

引入"松弛变量" 后的约束条件为:

5. KKT 条件[5]
KKT 条件是对最优分类超平面仅由支持向量决定, 与其它向量无关这个事实的一种数学描述. 实际上 KKT 条件是目前 SVM 训练算法迭代的判断条件. KKT条件描述如下: 
ai[yi((xi*w)+b)-1+ξi] = 0, i = 1,…,n
ξi(αi-C), i = 1,…,nKKT 
条件说明了这样一个事实: 在最终的分类器函数中, 每一个训练样本都对应着一个系数, 但是只有支持向量样本所对应的系数才有非零值, 而其它的系数都是零. 于是我们可以在训练算法中根据目前的分类器函数是否满足这样的条件而决定需要怎样使用样本对系数进行优化。

6. Platt-SMO 算法
SMO(Sequential Minimal Optimization, 序列最小化)算法, 通过将大优化问题分解成多个小优化问题来求解, 最终解出 SVM 所需要的 alpha 值.
SMO 在每次循环中选择两个 alpha 值进行优化, 一旦找到一对合适的 alpha, 就增大其中一个同时减小另一个. 直至所有的 alpha 值都无需优化为止.

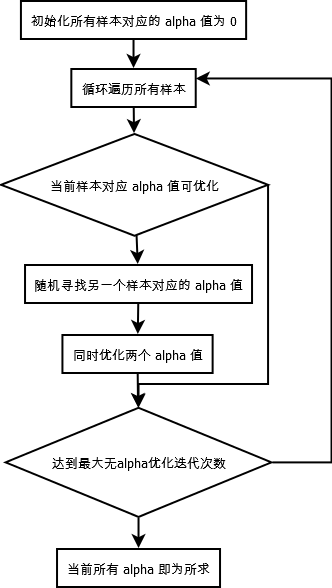
算法描述 (简化版 SMO)
(1). 每上样本对应的  alpha 值初始化为 0
(2). 对每个样本, 考虑其对应的 alpha 值是否可优化
(3). 如果可以优化, 则随机选择另一个样本对应的 alpha , 同时优化这两个 alpha
(4). 如果循环遍历所有样本达到指定迭代次数时, 都没有两个 alpha 值可以优化, 则结束
(5). 此时各个样本对应的 alpha 值即为所求

算法流程图 (简化版SMO)

代码 (简化版 SMO)

# -*- coding: utf-8 -* 
from numpy import *
from time import sleep

# 加载数据
# 数据按 tab 分隔, 最后一列是 标签
# 这里的标签按 -1, +1 进行划分
def loadDataSet(fileName):
    dataMat = []; labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = line.strip().split('\t')
        dataMat.append([float(lineArr[0]), float(lineArr[1])])
        labelMat.append(float(lineArr[2]))
    return dataMat,labelMat


# 在 0-m 中选择一个不等于 i 的随机数
# 参数 i 是第一个 alpha 的下标
# 参数 m 是
def selectJrand(i,m):
    j=i 
    while (j==i):
        j = int(random.uniform(0,m))
    return j


# 确保 aj 取值在 [L, H] 之间 
def clipAlpha(aj,H,L):
    if aj > H: 
        aj = H
    if L > aj:
        aj = L
    return aj


# 简化版的 SMO 函数
# 参数 dataMatIn, classLabels 为数据集及数据标签
# 参数 C, toler 为常数及容错率
# 参数 maxIter 为没有 alpha 改变情况下的最大循环次数
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
    dataMatrix = mat(dataMatIn); 
    labelMat = mat(classLabels).transpose()
    b = 0; 
    m,n = shape(dataMatrix)         # 得数据集的行和列

    # 所有 alpha 初始化为 0
    # 根据 KTT 条件, 在最终的分类器函数中，每一个训练样本都对应着一个系数，
    # 但是只有支持向量样本所对应的系数才有非零值，而其它的系数都是零
    alphas = mat(zeros((m,1)))      

    iter = 0                        # 记录没有 alpha 改变情况下的循环次数
    while (iter < maxIter):
        alphaPairsChanged = 0

        # 遍历每个样本
        for i in range(m):
            # fxi 为预测类别
            fXi = float(multiply(alphas,labelMat).T * 
                        (dataMatrix*dataMatrix[i,:].T)) + b
            Ei = fXi - float(labelMat[i])   # Ei 为预测类别与实际类别的话中有误差

            # 判断 alpha 是否可以更改进入优化过程
            # 如果误差很大, 就可以对 alpha 进行优化
            if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or \
               ((labelMat[i]*Ei >  toler) and (alphas[i] > 0)):
                
                j = selectJrand(i,m)  # 随机选择第 2 个 alpha  

                # 计算在 j 上的预测值和误差
                fXj = float(multiply(alphas,labelMat).T * 
                           (dataMatrix*dataMatrix[j,:].T)) + b
                Ej = fXj - float(labelMat[j])

                # 保证新计算的 alpha 在 0 与 C 之间
                alphaIold = alphas[i].copy(); 
                alphaJold = alphas[j].copy();
                if (labelMat[i] != labelMat[j]):
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])

                if L==H: print "L==H"; continue

                # 求 alpha[j] 的最优修改值
                eta = 2.0 * dataMatrix[i,:] * dataMatrix[j,:].T - 
                      dataMatrix[i,:]*dataMatrix[i,:].T - 
                      dataMatrix[j,:]*dataMatrix[j,:].T
                if eta >= 0: print "eta>=0"; continue

                # 检查 alpha[j] 是否是轻微改变, 如果是, 就结束本次循环
                # 因为改变的太小了, 没必要进行改变
                alphas[j] -= labelMat[j]*(Ei - Ej)/eta
                alphas[j] = clipAlpha(alphas[j], H, L) # alpha[j] 取值在 H, L 之间
                if (abs(alphas[j] - alphaJold) < 0.00001): 
                    print "j not moving enough"; 
                    continue

                # 对 alpha[i] 进行修改, 修改量与 alpha[j] 相同, 但方向相反
                alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])#

                # 给改变后的 alpha[i] 和 alpha[j] 设置常数项 
                b1 = b - Ei- 
                     labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - 
                     labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
                b2 = b - Ej- 
                     labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - 
                     labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T

                if (0 < alphas[i]) and (C > alphas[i]): 
                    b = b1
                elif (0 < alphas[j]) and (C > alphas[j]): 
                    b = b2
                else: 
                    b = (b1 + b2)/2.0

                alphaPairsChanged += 1
                print "iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged)

        if (alphaPairsChanged == 0): iter += 1  # 未成功更新过 alpha 的值
        else: iter = 0

    return b, alphas


if __name__ == "__main__":
    dataArr,labelArr = loadDataSet('testSet.txt')
    b,alphas = smoSimple(dataArr, labelArr, 0.6, 0.001, 40)

待补充
1. 完整 Platt SMO 算法加速优化
2. 核函数处理复杂数据

说明
本文为《Machine Leaning in Action》第六章(Support vector machines)读书笔记, 代码稍作修改及注释.

好文参考
1.《手把手教你实现SVM算法（一）》
2.《机器学习中的算法(2)-支持向量机(SVM)基础》
3.《SVM算法入门》
4.《拉格朗日乘子法和KKT条件》
5.《[转载]SVM 的学习和训练算法》