if a point is inside a square with mathematics
Algorithm to determine if a point is inside a square with mathematics (no hit test involved)
In the making of a game I am currently developing, I run into the problem of determining whether a point is inside or outside of a square.
And obviously the square can have any size and rotation. This task, which can be solved really quickly if you can rely on hit test, can become a nightmare if you try any other king of approach.
Some of you may suggest to use the ray casting algorithm, but when it comes a situation like “point in a square” it can also be done with some simple mathematics.
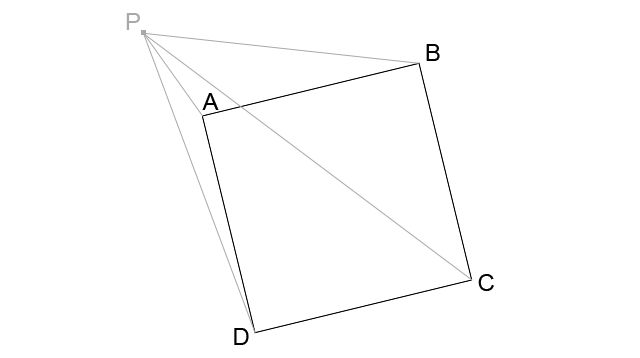
Look at this picture:
Given a square ABCD and a point P, we first need to build four triangles: ABP, BCP, CDP and DAP.
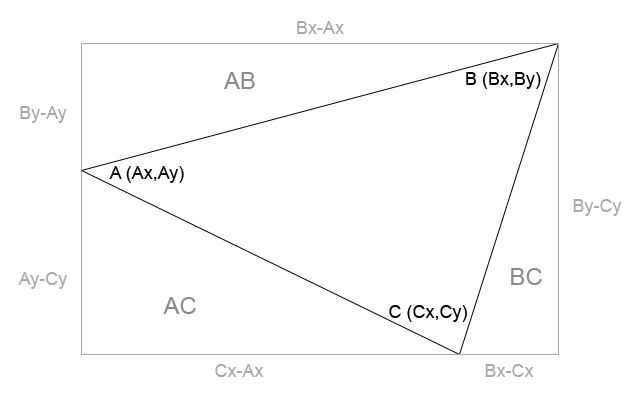
Now it’s time to determine the area of each triangle, and this may sound complicate unless you look at this picture:
We start by calculating the area of the rectangle which surrounds the triangle:
Area of Rectangle = (Bx-Ax)*(By-Cy) = BxBy-BxCy-AxBy+AxCy
Now, if we subtract from the area of the rectangle the areas of the three triangles called AB, BC and AC, we will get the area of the main triangle.
Area of triangle AB = (Bx-Ax)*(By-Ay)/2
Area of triangle BC = (Bx-Cx)*(By-Cy)/2
Area of triangle AC = (Cx-Ax)*(Ay-Cy)/2
Probably die hard mathematicians will be a bit upset at this time, because we could get negative areas, and the area of a triangle can’t be negative. That’s why mathematicians shouldn’t code, and you’re about to see why.
Let’s find the sum of the area of the three triangles:
AB+BC+AC = (BxBy-BxAy-AxBy+AxAy+BxBy-BxCy-CxBy+CxCy+CxAy-CxCy-AxAy+AxCy)/2
which can be simplified to:
BxBy+(-BxAy-AxBy-BxCy-CxBy+CxAy+AxCy)/2
Subtracting this area to the area of the rectangle will give us the area of the main triangle
Main triangle area = Area of Rectangle – Area of triangle AB – Area of triangle BC – Area of triangle AC
This means
Main triangle area = BxBy-BxCy-AxBy+AxCy-BxBy-(-BxAy-AxBy-BxCy-CxBy+CxAy+AxCy)/2
which can be simplified to:
(-BxCy-AxBy+AxCy+BxAy+CxBy-CxAy)/2
and also be written this way:
((CxBy-BxCy)-(CxAy-AxCy)+(BxAy-AxBy))/2
This is the final formula we need to calculate each of the four triangles ABP, BCP, CDP and DAP you can see in the first picture.
What’s now?
If the area of one (or more) triangles has a different sign than the other ones, the point isoutside the square. If all triangle areas have the same sign, the point is inside the square.
Obviously, you can even omit the division by two, since it does not affect the sign of the area.
If you are able to get square corners in the same direction, such as clockwise or counter-clockwise, you will just have to check if the areas are all respectively negative or positive.
Look at this script:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
|
package
{
import
flash
.
display
.
Sprite
;
import
flash
.
geom
.
Point
;
import
flash
.
events
.
Event
;
import
flash
.
events
.
MouseEvent
;
public
class
Main
extends
Sprite
{
private
var
A
:
Point
;
private
var
B
:
Point
;
private
var
C
:
Point
;
private
var
D
:
Point
;
var
squareCanvas
:
Sprite
=
new
Sprite
(
)
;
public
function
Main
(
)
{
squareCanvas
=
new
Sprite
(
)
;
addChild
(
squareCanvas
)
;
drawSquare
(
null
)
;
stage
.
addEventListener
(
MouseEvent
.
CLICK
,
drawSquare
)
;
addEventListener
(
Event
.
ENTER_FRAME
,
update
)
;
}
private
function
drawSquare
(
e
:
MouseEvent
)
:
void
{
var
squareSide
:
Number
=
150
+
Math
.
random
(
)
*
100
;
var
squareDiagonal
:
Number
=
squareSide*
Math
.
sqrt
(
2
)
;
var
squareAngle
:
Number
=
Math
.
random
(
)
*
2
*
Math
.
PI
;
A
=
new
Point
(
320
-
Math
.
cos
(
Math
.
PI
/
4
+
squareAngle
)
*
squareSide
,
240
-
Math
.
sin
(
Math
.
PI
/
4
+
squareAngle
)
*
squareSide
)
;
B
=
new
Point
(
320
-
Math
.
cos
(
Math
.
PI*
3
/
4
+
squareAngle
)
*
squareSide
,
240
-
Math
.
sin
(
Math
.
PI*
3
/
4
+
squareAngle
)
*
squareSide
)
;
C
=
new
Point
(
320
-
Math
.
cos
(
Math
.
PI*
5
/
4
+
squareAngle
)
*
squareSide
,
240
-
Math
.
sin
(
Math
.
PI*
5
/
4
+
squareAngle
)
*
squareSide
)
;
D
=
new
Point
(
320
-
Math
.
cos
(
Math
.
PI*
7
/
4
+
squareAngle
)
*
squareSide
,
240
-
Math
.
sin
(
Math
.
PI*
7
/
4
+
squareAngle
)
*
squareSide
)
;
}
private
function
update
(
e
:
Event
)
:
void
{
var
mousePoint
:
Point
=
new
Point
(
mouseX
,
mouseY
)
;
squareCanvas
.
graphics
.
clear
(
)
;
if
(
isInsideSquare
(
A
,
B
,
C
,
D
,
mousePoint
)
)
{
squareCanvas
.
graphics
.
lineStyle
(
1
,
0xFF0000
)
;
}
else
{
squareCanvas
.
graphics
.
lineStyle
(
1
,
0x000000
)
;
}
squareCanvas
.
graphics
.
moveTo
(
A
.
x
,
A
.
y
)
;
squareCanvas
.
graphics
.
lineTo
(
B
.
x
,
B
.
y
)
;
squareCanvas
.
graphics
.
lineTo
(
C
.
x
,
C
.
y
)
;
squareCanvas
.
graphics
.
lineTo
(
D
.
x
,
D
.
y
)
;
squareCanvas
.
graphics
.
lineTo
(
A
.
x
,
A
.
y
)
;
}
public
function
triangleArea
(
A
:
Point
,
B
:
Point
,
C
:
Point
)
:
Number
{
return
(
C
.
x*
B
.
y
-
B
.
x*
C
.
y
)
-
(
C
.
x*
A
.
y
-
A
.
x*
C
.
y
)
+
(
B
.
x*
A
.
y
-
A
.
x*
B
.
y
)
;
}
public
function
isInsideSquare
(
A
:
Point
,
B
:
Point
,
C
:
Point
,
D
:
Point
,
P
:
Point
)
:
Boolean
{
if
(
triangleArea
(
A
,
B
,
P
)
>
0
||
triangleArea
(
B
,
C
,
P
)
>
0
||
triangleArea
(
C
,
D
,
P
)
>
0
||
triangleArea
(
D
,
A
,
P
)
>
0
)
{
return
false
;
}
return
true
;
}
}
}
|
It applies this logic to calculate triangle area (lines 44-46) and determine if a point is inside a square (lines 47-52).
And this is the result:
Move the mouse and the square will turn red when the pointer is inside of it. Click to generate another random square.
Download the source code.