《An Efficient Implementation of Trie Structures 》论文解读
<由于本文从word中粘贴过来,故排版比较乱,可下载附件中的pdf版>
引言
在许多的信息检索应用中,很多地方都需要以前缀匹配的方式来检索输入的字符串。比如:编译器的词法分析、目录检索、拼写检查、中文分词的词库等自然语言处理相关的应用。为了提高检索的效率,我们通常把字符串构建成Trie树的形式。Trie树的每个结点是一个数组,数组中存储着下一个结点的索引信息。如对K=set{baby,bachelor,badge,jar}建立Trie树,结构如下图:
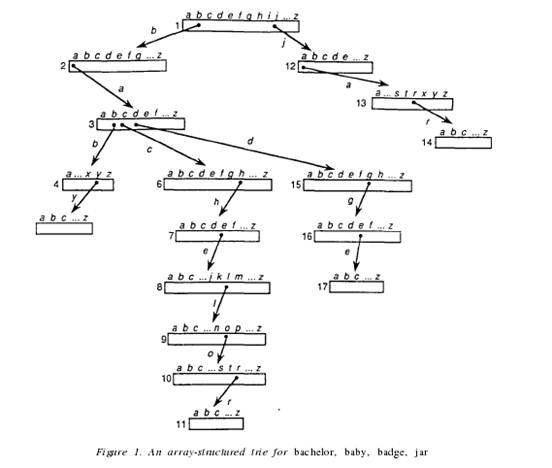
从上图中可以看出,基于Trie树对字符串进行检索、删除、插入是非常快的,但是空间开销却随着字符种类数和结点个数成比例增长,而且这种增加是成指数的增长。为了解决空间闲置问题,我们最容易想到的压缩方法就是把Trie树结点中的数组换成链表,这样就避免了数组中出现大量的NULL值情况,通俗地说,就是用左孩子右兄弟的方式来维持Trie树,如下图:
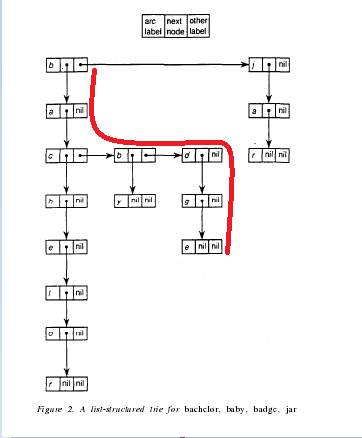
但是这样却带来了检索效率的降低,特别是一个结点有多个子结点的时候,例如,图中结点b的孩子结点a有{c,b,d}三个孩子,这样在检索badge的时候,就需要遍历结点b-a-c-b-d-g-e(如上图红色的线条。)才能检索到。
本文提出了一种新的压缩方法,把Trie树压缩到两个一维数组BASE和CHECK中,数组BASE和CHECK合称Double-Array。在Double-Array中,非空的结点n通过BASE数组映射到CHECK数组中。也就是说,没有任何两个非空的结点会通过BASE数组映射到CHECK数组的同一个位置。Trie树中的每条边都能通过Double-Array以o(1)的复杂度检索到。换句话说:如果一个字符串的长度为k,那么最多只需要o(k)的复杂度就可以完成检索。当字符串的数量众多时,使Double-Array中的空间尽可能充分利用就变得十分重要了。为了使Trie树能够满足存储海量字符串的需求,Double-Array中只储存字符串中的前缀,然后把字符串的剩余部分存储到字符数组中,我们把这个字符数组称为tail数组。通过Double-Array和tail数组的组合,就达到了尽可能节约内存,同时又能区别出任意两个字符串的目的。
详细解说DATrie(Double-Array Trie)
Trie是一种树形的数据结构。Trie中从根结点到叶子结点的每条路径代表着存储在Trie中的一个字符串(key)。这也就是说,路径中连接两个结点的边代表着一个字符。这跟我们通常了解到的把字符信息储存到结点中的树是不一样的。为了避免类似于the 和then这样的字符串在Trie中造成混淆,我们引入一个特别的字符# 用来表示每个字符串的结束。这样插入the和then到Trie中时,实际上是插入the# 和then# 。
为了更清晰地解说Trie,我们作如下的定义:
K 代表形成Trie的字符串集合。Trie由结点和连接结点的边(arc)组成。结点由Double-Array的下标来标记,边则是由字符来标记,如果一条边从结点n到结点m被标记成a,那么我们可以定义如下的函数g(n,a)=m 。
对于集合K中的一个字符串S在Trie中形成的一条路径P,如果路径P中有结点m满足g(n,a)=m ,使得在Trie中检索S时,检索到字符a就已经能够将字符串S与Trie中的其它字符串区别开来,那么结点m称为separate node 。例如Figure 3中结点15、结点5、结点6、结点4都是separatenode。
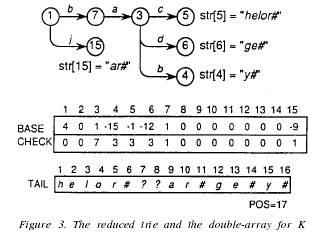
从separatenode到叶子结点之间的字符串称之为结点m的 single string.用STR[m]表示。例如图Figure3中str[5]、str[6]都是single string.从S中删除singlestring后剩余的部分称为tail . (这里我没没理解清楚,只是觉得tail与single string是一个意思,就是STR[m])树中只由从根结点到separatenode 之间的边组成的部分称为reduced trie。Figure3就是reducedtrie的一个例子,用Double-Array和字符数组来存储tail信息。TAIL数组中的问号标志?用来表示废弃的空间(原来存储过信息,后来该位置不用了)。关于Double-Aarray 和TAIL的用法将会在插入操作和删除操作中详细解释。
在Figure3 中,Double-Array和reducedtrie 的关系如下:(到这里就很容易理解了,reduced trie表示的是一种结构,而Double-Array则表示reduced-trie这种结构的存储方式)
第一、如果reduced trie中的一条边满足g(n,a)=m,那么对应到Double-Array中的实现则有:BASE[n]+a=m, CHECK[m]=n (对于边的标识字符,有如下约定 #=1 a=2 b=3 c=4…. )
第二、如果结点m是seprate node,由此得到的tail字符串STR[m]=b1b2....bh那么有 BASE[m]<0 设p=-BASE[m],则TAIL[p]=b1 ,TAIL[p+1]=b2 …… TAIL[p+h-1]=bh
以上两条关系将贯穿本文。
例如:
对于关系一:
Figure 3中根结点1到结点7 及字符b :有g(1,b)=7 -> BASE[1]+b = 4+3=7 (b=3) CHECK[7]=1
对于关系二:
Figure 3中结点5,BASE[5]=-1 ,对应到TAIL数组中p=-BASE[5]=1 TAIL[1]=h TAIL[2]=e TAIL[3]=l
那么从根结点到结点5,到STR[m],我们就可以检索到bachelor#这个字符串了。
实际上,有以下几点是需要提出来的:
一、结点1永远是Trie的根结点,所以Trie的插入和查找操作都是从BASE[1]开始。
二、CHECK[m]=n 所表达的意思是:结点m的父结点是n . 所以如果表述为father[m]=n可能更清楚一些。
三、在Double-Array中,除CHECK[1]之外,如果CHECK[m]=0,则表示结点m是孤岛,是可用的。Double-Array实际就就是通过g(n,a)=m把这些孤岛连接成reduced trie这种树形结构。这一点在理解trie的insertion操作时会有帮助。
字符串的查找
通过Double-Array对字符串进行查找是非常快捷的。例如:用Double-Array查找Figure3中的字符串bachelor# 。执行步骤如下:
步骤1:从根结点1开始,由于我们已经定义b=3,所以:
BASE[n]+a=BASE[1]+b=4+3=7
我们也观察到CHECK[7]=1 所以这是一条通路,能往下走。
步骤2:由于BASE[1]=7>0,我们继续。用7作为BASE数组新的下标,由于bachelor#的第二个字符是a,所以
BASE[n]+a=BASE[7]+2=1+2=3 . 而且CHECK[3]=7
步骤3,4:按如上的方式继续,由于已经定义了c=4,我们有:
BASE[3]+c=BASE[3]+4=1+4=5而且CHECK[5]=3
步骤5:BASE[5]=-1 ,表示剩下的字符串被存储到了TAIL数组中。从TAIL[ -BASE[5]]=TAIL[1]开始,检索剩下的字符串就可以用最常用的字符串比较方法了。
反复体会这个过程,我们能够发现:在trie中检索字符串只是直接地在数组中定位下一个节点。没有类似于广度或者深度优先搜索这样的查找操作。这种方式使得字符串的查找变得十分直截了当。
实际上在编写代码的时候,查找操作还是有一些细节需要注意的。这些细节就只能在代码里面体会了。
插入操作
DATrie的插入操作也是相当的直截了当。在插入过程中,无外乎以下四种情况:
Case 1 : 插入字符串时树为空。
Case 2: 插入字符串时无冲突。
Case 3: 插入字符串时出现不用修改现有BASE值的冲突,但是需要把TAIL数组中的字符信息展开到BASE数组中。(解决有公共前缀字符串的问题)
Case 4: 插入字符时出现需要修改现有BASE值的冲突。(位置占用冲突)
冲突的出现意味着在double-array中两个不同的字符通过g(n,a)得到了同样的m值,换话话说,两个不同的父结点拥有了同一个孩子(表现在double-array中就是两个字符争夺数组中的同一个空间位置)。上述的四种情况将通过在一棵空的Trie (Figure 4)中插入bachelor# (Case1) ;jar#(Case 2); badge#(Case 3) baby#(Case 4) 一一演示出来。我们定义DA_SIZE表示double-array中CHECK数组的最大长度(BASE数组与CHECK数组大小相等),并且BASE数组和CHECK数组的长度可以动态地增加,数组默认以0来填充。
Case 1 : 插入字符串时Trie树为空。
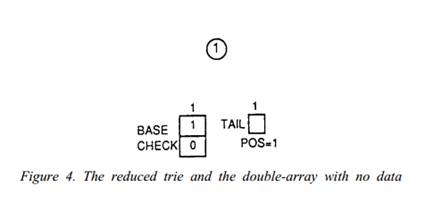
(树为空时,BASE[1]=1,CHECK[1]=0, TAIL数组的起始位置POS=1; 这其实也就是编码时Trie的初始化。)
插入单词bachelor#将按如下步骤进行;
步骤1:从double-array中BASE数组的下标1开始(也就是树的根结点)b的值为3,所以
BASE[1]+b=1+3=4, CHECK[4]=0≠1
步骤2:CHECK[4]=0表示结点4是separate node,由于b已经通过g(1,’b’)=4这种方式存储到double-array中了,所以单词剩下的部分achelor#直接插入到TAIL数组中即可。
步骤3:赋值BASE[4]=-POS=-1 表明achelor#将从POS位置开始插入到TAIL数组中。
步骤4:赋值POS=1+length(‘achelor#’) =9,表示下一个字符串存储到TAIL数组的起始位置。
Figure 5 显示了插入bachelor#后reduced trie 和double-array的状态。
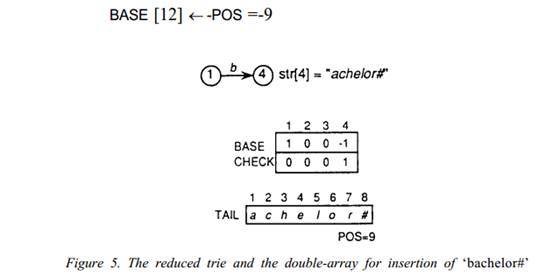
Case 2: 插入字符串时无冲突。
按如下的步骤插入单词jar#
步骤1:从double-array的BASE数组下标1开始,由于已经定义j=11
BASE[1]+j=1+11=12 CHECK[12]=0≠1
步骤2:CHECK[12]=0表示结点12是空结点,可以将剩余的部分ar#直接插入到TAIL数组中去。插入的起始位置POS=9
步骤3:赋值BASE[12]=-POS=-9,同时赋值CHECK[12]=1 表明结点12是结点1的子结点。
步骤4:设置POS=12 , 表示下一个字符串存储到TAIL数组的起始位置。
实际上通过插入bachelor#和jar#很难看出Case 1 和Case 2之间的不同,所以其实他们的不同也是只概念上不同,而非操作上的不同。(由于Case 1和Case 2的实现非常简单,也无需纠结于此。我们可认为这是作者玩的文字游戏)插入jar#后reduced trie和double-array的状态如图Figure 6所示:
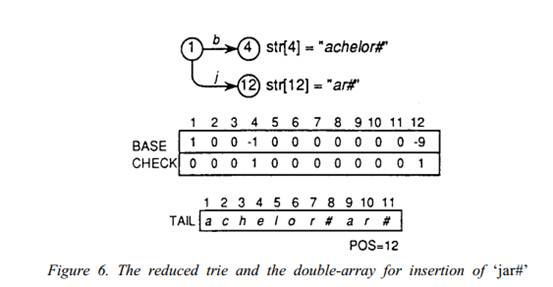
为了研究Case 3和Case 4两种情况,我们需要定义一个函数X_CHECK(LIST)其功能是返回一个最小的整数q,q满足如下条件:q>0 并且对于LIST中的每一个元素c,有CHECK[q+c]=0。(对于X_CHECK函数,我们可以分两步理解,第一步:CHECK [m]=n表示结点m的父结点是n;第二步:设LIST={c1,c2,…cn},我们可认为q+c1,q+c2 … q+cn都是将要被领养的孩子,而这些孩子被领养必须有一个条件:没有父亲,而CHECK[q+c]=0即表示结点q+c没有父结点)
Case 3:公共前缀冲突
(公共前缀冲突是我自己起的名字,上文已经交代过,这种冲突的特点是无需修改以有的结点位置,即BASE数组中的非零值,只是把TAIL数组中的字符“解压缩”到double-array中)
通过插入单词badge#,我们可以认识到这种冲突。
步骤1:从BASE[1]开始,由于b=3,所以:
BASE[1]+b=1+3=4, CHECK[4]=1
CHECK[4]的非零值表示有一条边从结点CHECK[4](也就是结点1)到到结点4,(就是Figure 6中的字符b所标识的边)
步骤2:如果BASE[1]>0,我们直接到下一个结点就可以了,但是这里:
BASE[1]=-1
BASE[1]的值为负表明在trie中的查询已经结束,我们需要到TAIL数组中进行字符串比较。
步骤3:从pos=-BASE[1]=1作为TAIL数组的起始位置,比较achelor#和待插入字符串的剩余部分,也就是adge#。当两个字符串的比较失败,就用步骤4、5、6的方式把他们的公共前缀插入到double-array中。
步骤4:申明一个临时变量TEMP,并把-BASE[1]保存到这个临时变量中
TEMP à -BASE[1]
步骤5:计算字符串achelor#和adge#的公共前缀字符a的X_CHECK[{‘a’}]值:
CHECK[q+a]= CHECK[1+2]=CHECK[3]=0所以q=1
(q是从1开始递增试出来的)
这样1就作为了BASE[4]新的候选值,CHECK[3]=0也表明结点3是可以作为结点4的子结点。这样结点4和结点3就可以通过g(4,a)=g(4,2)=3关系式,把字符a存储到double-array中了。
步骤6:给BASE[4]赋新的值:
BASE[4]=1 , 同时赋值CHECK[BASE[4]+a]=CHECK[1+2]=CHECK[3]=4
这样trie中就有一条新的边诞生了,边从结点4开始到结点3结束,边的标识符号为a。
注意:由于本例中只有一个公共前缀,所以步骤5和步骤6没有重复。但是如果有多个公共前缀,步骤5、6会重复执行多次,直到公共前缀都处理完。
步骤7:为了存储剩下的字符串chelor#和dge#,我们需要为BASE[3]寻找新的候选值,使得字符c和字符d能够存储到double-array中,其计算方法为X_CHECK[{‘c’,’d’}]
对于’c’ : CHECK[q+’c’]=CHECK[1+4]=CHECK[5]=0 满足条件
对于’d’: CHECK[q+’d’]=CHECK[1+5]=CHECK[6]=0 满足条件
所以q=1, 赋值BASE[3]=1
步骤8:以字符串chelor#的首字符作为参数,计算字符串在BASE和CHECK数组中的结点编号。通过该结点可以在TAIL中定位到helor# 。
BASE[3]+’c’=1+4=5
BASE[5]=-TEMP=-1 ,CHECK[5]=3
通过BASE数组建立到TAIL数组的引用,通过CHECK数组确定状态3到状态5的边。
(这里“状态”与“结点”是同一个意思)
步骤9:把字符串的剩余部分”helor#”存储到TAIL数组中,其起始位置为-BASE[5]=1,只是TAIL[7]和TAIL[8]两个位置就变成空位了。(实际编程会有所不同)
步骤10:对于新插入字符串剩余部分”dge#”:
BASE[3]+’d’=1+5=6 ;
BASE[6]=-POS=-12
CHECK[6]=3
然后把”ge#”存储到TAIL数组中。
步骤11:最后更新POS为下一次插入的起始位置,也就是TAIL中已用空间的的末尾。
POS=12+length[‘ge#’]=12+3=15
总的来说,当冲突发生了,字符串中产生冲突的公共前缀需要从TAIL数组中提取出来,然后存储到double-array中。冲突字符串(包括新插入的字符串)在double-array中关联的值(满足条件BASE[n]<0)都要转移到最近的空结点位置。(参考Figure 7)
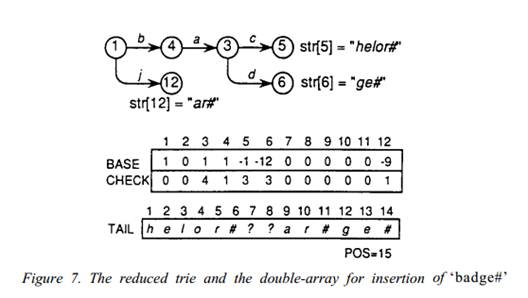
Case 4:抢占位置引发的冲突
(现在进入到整篇文章最核心的地方了,也就是DATrie最难的地方)
就像Case 3 一样,BASE数组中的值必须进行修改才能解决冲突。插入”baby#”的步骤演示如下:
步骤1:根结点在BASE数组的下标1位置,所以从BASE[1]开始。
对于baby#中前三个字符而言,BASE和CHECK中的值如下;
BASE[1]+’b’=1+3=4, CHECK[4]=1
BASE[4]+’a’=1+2=3, CHECK[3]=4
BASE[3]+’b’=1+3=4, CHECK[4]=1≠3
CHECK[4]的计算结果出现前后不一致的现象表明有一个状态没有被考虑到。这也意味着结点1或者结点3的BASE值需要进行修改。(这里可以这样理解:结点4作为子结点被父结点1和父结点3争夺,我们有两种方法解决冲突:结点1放弃孩子或者结点3放弃孩子。如果是结点1让步,那么就需要修改BASE[1],如果结点3让步,那么就需要修改BASE[3])
步骤2:申明变量TEMP_NODE1,并赋值TEMP_NODE1 = BASE[3]+’ b’=1+3=4
如果CHECK[4]=0,那么直接把剩余部分存储到TAIL中就可以了,但是事与愿违。
步骤3:分别把从结点3和结点1引出的边存储到list中,通过Figure 7有:
list[3]={‘c’,’d’}
list[1]={‘b’,’j’}
步骤4:由于我们的目的是让新插入的字符串与结点3进行关联(实际上修改BASE[1]或者修改BASE[3]哪种方案最优,是通过工作量来进行衡量的。因为修改BASE[n]同时需要修改BASE[n]的子结点位置,所以子结点数越少,工作量就越少),即字符’b’将给结点3带来一个新子结点,所以从结点3引出的边的个数需要加1。所以我们:
Compare(length(list[3])+1,list[1]) =compare(3,2)
如果length(list[3]+1)<length(list[1]),那么我们就修改结点3的BASE值,但是由于length(list[3]+1)≥length(list[1]) ,我们修改结点1。
步骤5:申明变量TEMP_BASE,赋值
TEMP_BASE=BASE[1]=1
并且用X_CHECK计算BASE[1]新的候选值:
X_CHECK(‘b’): CHECK[q+’b’]=
CHECK[1+3]=CHECK[4]≠0
CHECK[2+3]=CHECK[5]≠0
CHECK[3+3]=CHECK[6]≠0
CHECK[4+3]=CHECK[7]=0满足条件
而且对于
X_CHECK(‘j’): CHECK[q+’j’]=
CHECK[4+11]=CHECK[15]=0满足条件
所以q=4合法,赋值 BASE[1]=4
步骤 6:对于’b’ ,把将被修改的状态值存储到临时变量中:
TEMP_NODE1 TEMP_BASE+ ‘b’=1+3=4
TEMP_NODE2 BASE[1]+ ‘b’=4+3=7
把BASE值从旧的状态更新到新的状态:
BASE[TEMP_NODE2]---- BASE[TEMP_NODE1] 也就是
BASE[7]=BASE[4]=1
同时把CHECK值也更新
CHECK [TEMP_NODE2 ] =CHECK [7] ---- CHECK [4]=1
(这里其实也好理解,对于结点1,原来的子结点为4和12,BASE值更新后,子结点随之变成7和15,把原来结点4和结占12的BASE及CHECK值转移到结点7和结点15就完成了子结点的更新了,如果子结点还有孩子,比如结点4的子结点为3,那么更新后,结点3的父结点将不再是结点4,而变成结点7)
步骤7:由于
BASE[TEMP_NODE1]=BASE[4]=1>0 <结点4有子结点>
把结点4的所有子结点的父结点更新为结点7
CHECK [ BASE[4]+2] = CHECK [l+2]= CHECK [3] TEMP_NODE2 =7
步骤8:结点1的子结点从结点4变成结点7后,结点4已经空置了。所以需要进行标记:
BASE[4]=0
CHECK[4]=0
同样地,对于’j’:<导向子结点12的边>
步骤9:把将被修改的状态值存储到临时变量中:
TEMP_NODE1 TEMP_BASE+ ‘j’=1+11=12
TEMP_NODE2 BASE[1]+ ‘j’=4+11=15
把BASE值从旧的状态更新到新的状态:
BASE[TEMP_NODE2] ----BASE[TEMP_NODE1] 也就是
BASE[15]=BASE[12]=-9
同时把CHECK值也更新
CHECK [ TEMP_NODE2 ]=CHECK [15] ---- CHECK [12]=1
步骤10:由于
BASE[TEMP_NODE1]=BASE[12]=-9<0
即BASE[12]没有子结点,所以只需要把结点12置空就可以了。
BASE[12]=0
CHECK[12]=0
这样的话由baby中的字符’b’产生的冲突就被解决了。最后,把新插入字符串的剩余部分存储到TAIL数组中就OK了。
步骤11:从产生冲突的那个结点(即结点3)开始,重新计算由字符’b’得到的新结点,并把它存储到临时变量TEMP_NODE中
TEMP_NODE=BASE[3]+’b’=4
步骤12:把字符串在TAIL数组存储的起始位置存储到BASE数组中
BASE[TEMP_NODE]=BASE[4]=-POS=-15
步骤13:把字符串的剩余部分存储到TAIL数组中
TAIL[POS]=TAIL[15]+’y#’
步骤14:更新POS为下一次插入的起始位置,也就是TAIL中已用空间的的末尾。
POS=15+length[‘y#’]=15+2=17
小结一下,当double-array中发生了位置占用冲突,我们需要修改产生冲突结点的父结点BASE值,对于这两个父结点(对应到程序中就是pre和CHECK[cur]),具体修改哪一个取决于其子结点的个数,子结点个数少的父结点将被修改。这样冲突就可以得到解决,字符串也能顺利地插入到trie中了。插入后的结果如Figure 3所示:
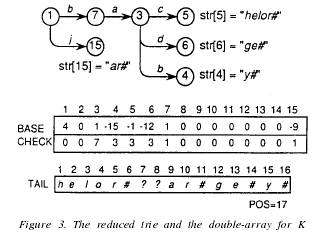
Trie的删除操作
Trie的删除操作也是非常简单。把前面的插入熟悉后,自己看论文《An Efficient Implementation of TrieStructures》就能懂了,这里也就不继续解说了。
论文剩下的部分就是性能的评估,感兴趣的可以自行了解。最后有实现的伪代码,还是有一定的参考价值的。
其实,字符串处理的相关数据结构,无非是利用了字符串的前缀和后缀信息。比如SuffixArray(后缀数组)利用的是后缀信息,Trie树,利用的是前缀信息。
理解DATrie树,我们应该认识到,DATrie是一种数据结构,理解数据结构,只需要理解数据结构对数据的”增删改查”四种操作就可以了。对于DATrie,其核心在于理解插入操作;而插入操作的难点在于理解BASE数组和CHECK数组,BASE数组和CHECK数组的难点在于插入时出现冲突的解决方案。所以,DATrie树的难点只有一个:冲突解决方案。
在学习的过程,反复在纸上画出trie的结构,自己推理double-array值对于理解trie是非常有帮助的。
最后提供一个测试样例:“ba” “bac” ”be”“bae”,因为没有这个样例,我在编码的时候被困了好几天。
在我的笔记本电脑上<i5+4G内存+32位win7+2.4GZ>,用DATrie 插入38万数量的词典,用时240084毫秒,查询用时299毫秒。
最后还是贴出代码吧!
package com.vancl.dic;
import java.io.DataInputStream;
import java.io.DataOutputStream;
import java.io.File;
import java.io.FileInputStream;
import java.io.FileOutputStream;
import java.io.RandomAccessFile;
import java.util.ArrayList;
import java.util.Arrays;
public class DATrie {
final int DEF_LEN=1024;
final char END_TAG='#';//#在CWC中的value=1
int[] base = new int[DEF_LEN];
int[] check = new int[DEF_LEN];
char[] tail =new char[DEF_LEN];
int tailPos;
public DATrie(){
base[1]=1;tailPos=1;
Hash.put(END_TAG,1);
}
/*
* 查找一个词是否在Trie树结构中
* */
public boolean retrieval(String word){
//执行查询操作
int pre=1,cur=0;
for(int i=0;i<word.length();i++){
cur=base[pre]+GetCode(word.charAt(i));
if(check[cur]!=pre)return false;
//到tail数组中去查询
if(base[cur]<0 ){
int head=-base[cur];
return MatchInTail(word, i+1, head);
}
pre=cur;
}
//这一句是关键,对于一个串是另一个字符串 子串的情况
if(check[base[cur]+GetCode(END_TAG)]==cur)return true;
return false;
}
public void insert(String word){
word+=END_TAG;
for(int i=0,pre=1,cur;i<word.length();i++){
cur=base[pre]+GetCode(word.charAt(i));
//容量不够的时,扩容
if(cur>=base.length)extend();
//空白位置,可以添加,这里需要注意的是如果check[cur]=0,则base[cur]=0成立
if( check[cur] == 0){
check[cur]=pre;
base[cur]=-tailPos;
toTail(word,i+1); //把剩下的字符串存储到tail数组中
return;//当前词已经插入到DATire中
}
//公共前缀,直接走
if(check[cur]==pre && base[cur]>0 ){
pre=cur;continue;
}
//遇到压缩到tail中的字符串,有可能是公共前缀
if(check[cur] == pre && base[cur]<0 ){
//是公共前缀,把前缀解放出来
int new_base_value,head;
head=-base[cur];
//插入相同的字符串
if(tail[head]==END_TAG && word.charAt(i+1)== END_TAG)
return ;
if(tail[head]==word.charAt(i+1)){
int ncode=GetCode(word.charAt(i+1));
new_base_value=x_check(new Integer[]{ncode});
//解放当前结点
base[cur]=new_base_value;
//连接到新的结点
base[new_base_value+ncode]=-(head+1);
check[new_base_value+ncode]=cur;
//把边推向前一步,继续
pre=cur;continue;
}
/*
* 两个字符不相等,这里需要注意"一个串是另一个串的子串的情况"
* */
int tailH=GetCode(tail[head]),nextW=GetCode(word.charAt(i+1));
new_base_value=x_check(new Integer[]{tailH,nextW});
base[cur]=new_base_value;
//确定父子关系
check[new_base_value+tailH] = cur;
check[new_base_value+nextW] = cur;
//处理原来tail的首字符
base[new_base_value+tailH] = (tail[head] == END_TAG) ? 0 : -(head+1);
//处理新加进来的单词后缀
base[new_base_value+nextW] = (word.charAt(i+1) == END_TAG) ? 0 : -tailPos;
toTail(word,i+2); return;
}
/*
* 冲突:当前结点已经被占用,需要调整pre的base
* 这里也就是整个DATrie最复杂的地方了
* */
if(check[cur] != pre){
int adjustBase=pre;
Integer[] list=GetAllChild(pre);//父结点的所有孩子
Integer[] tmp=GetAllChild(check[cur]);//产冲突结点的所有孩子
int new_base_value;
if(tmp!=null && tmp.length<=list.length+1){
list=tmp;tmp=null;
adjustBase=check[cur];
new_base_value=x_check(list);
}else{
//由于当前字符也是结点的孩子,所以需要把当前字符加上
list=Arrays.copyOf(list, list.length+1);
list[list.length-1]=GetCode(word.charAt(i));
new_base_value=x_check(list);
//但是当前字符 现在并不是他的孩子,所以暂时先需要去掉
list=Arrays.copyOf(list, list.length-1);
}
int old_base_value=base[adjustBase];
base[adjustBase]=new_base_value;
int old_pos,new_pos;
//处理所有节点的冲突
for(int j=0;j<list.length;j++){
old_pos=old_base_value+list[j];
new_pos=new_base_value+list[j];
/*
* if(old_pos==pre)pre=new_pos;
* 这句代码差不多花了我3天的时间,才想出来
* 其间,反复看论文,理解DATrie树的操作过程。
* 动手在纸上画分析DATrie可能的结构。最后找到
* 样例:"ba","bac","be","bae" 解决问题
* */
if(old_pos==pre)pre=new_pos;
//把原来老结点的信息迁移到新节点上
base[new_pos]=base[old_pos];
check[new_pos]=check[old_pos];
//有后续,所有孩子都用新的父亲替代原来的父亲
if(base[old_pos]>0){
tmp=GetAllChild(old_pos);
for (int k = 0; k < tmp.length; k++) {
check[base[old_pos]+tmp[k]] = new_pos;
}
}
//释放废弃的节点空间
base[old_pos]=0;
check[old_pos]=0;
}
//冲突处理完毕,把新的单词插入到DATrie中
cur=base[pre]+GetCode(word.charAt(i));
if(check[cur]!=0){
System.err.println("collision exists~!");
}
base[cur]=(word.charAt(i)==END_TAG)?0:-tailPos;
check[cur]=pre;
toTail(word,i+1);return;//这里不能忘记了
}
}
}
//到Tail数组中进行比较
private boolean MatchInTail(String word,int start,int head){
word+=END_TAG;
while(start<word.length()){
if(word.charAt(start++)!=tail[head++])return false;
}
return true;
}
/*
* 寻找最小的q,q要满足的条件是:q>0 ,并且对于list中所有的元素都有check[q+c]=0
* */
private int x_check(Integer[] c){
int cur,q=1,i=0;
do{
cur = q + c[i++];
if(cur >= check.length) extend();
if(check[cur] != 0 ){
i=0;++q;
}
}while(i<c.length);
return q;
}
//寻找一个节点的所有子元素
private Integer[] GetAllChild(int pos){
if(base[pos]<0)return null;
ArrayList<Integer> c=new ArrayList<Integer>();
for(int i=1;i<=Hash.size();i++){
if(base[pos] + i >= check.length)break;
if(check[base[pos]+i] == pos)c.add(i);
}
return c.toArray(new Integer[c.size()]);
}
public Integer GetCode(char ch){
return Hash.GetCode(ch);
}
//将字符串的后缀存储到tail数组中
private void toTail(String w,int pos){
//如果容量不足,就扩容
if(tail.length-tailPos < w.length()-pos)
tail=Arrays.copyOf(tail, tail.length<<1);
while(pos<w.length()){
tail[tailPos++]=w.charAt(pos++);
}
}
private void extend(){
base=Arrays.copyOf(base, base.length<<1);
check=Arrays.copyOf(check, check.length<<1);
}
}
Hash.java
package com.vancl.dic;
import java.util.HashMap;
public class Hash {
private static final HashMap<Character,Integer> hash=
new HashMap<Character,Integer>();
public static int GetCode(char ch){
if(!hash.containsKey(ch)){
hash.put(ch, hash.size()+1);
}
return hash.get(ch);
}
public static void put(char ch,int value){
hash.put(ch, value);
}
public static int size(){
return hash.size();
}
}
Test程序:
package com.vancl.dic;
import junit.framework.Assert;
import org.junit.Test;
public class DATrieTest {
@Test
public void testInsert(){
String[] s={"bachelor","jar","badge","baby"};
String[] s2={"ba","bac","be","bae"};
DATrie dat=new DATrie();
for (String string : s2) {
dat.insert(string);
}
for (String string : s2) {
Assert.assertEquals(true, dat.retrieval(string));
}
}
}
参考文档:
《An effcient Implements of Trie Structures》
http://blog.csdn.net/dingyaguang117/article/details/7608568
http://www.iteye.com/topic/391892
由于文章是从word中粘贴出来的,排版效果很难看,这里我转成了pdf,可以在附件中下载。