CRC原理及实现
CRC(Cyclic Redundancy Check)中文名是循环冗余校验,由于计算简单等,被广泛用于数据校验,具有很强的检错能力。最常见的有网络传输中信息的校验,但同样的道理,我们也可以将其应用到软件中,如:winrar对文件的校验。另外,我们还可以将它应用到软件上面来保护软件被恶意修改,还可以用在内存动态校验上面。用途多多,变通方式也不一,但基本原理都是这个。
CRC算法的是以GF(2)(2元素伽罗瓦域)多项式算术为数学基础的,嗯,听着是有点恐怖,但别被吓着了,其实说白了也很简单。虽然我们大可跳过数学部分用计算机的术语来描述,但我依旧不想跳过这部分,以防后来者忽略数学在计算机中的重要性,能看到数学在计算机的应用也能鼓舞起他们学习数学的信心。无可置疑,很多算法都源于数学,都以数学为支撑,数学功底在一定程度上决定你能走到的高度。
首先,我们来介绍一下2元素伽罗瓦域及其基本运算。
GF(2)多项式中只有一个变量x,其系数也只有0和1,如:
1*x^6 + 1*x^5 + 0*x^4 + 0*x^3 + 1*x^2 +1*x^1 + 1*x^0 即: x^6 + x^5 + x^2 + x + 1 (x^n表示x的n次幂)
GF(2)的多项式加减运算其实都一样:模2运算,运算时不考虑借位和进位。咋一听好像很高级似的,其实说白了就是异或运算。
0 + 0 = 0 0 - 0 = 0 0 + 1 = 1 0 - 1 = 1 1 + 0 = 1 1 - 0 = 1 1 + 1 = 0 1 - 1 = 0
比如:P1 = x^6 +x^5 + x^2 + x + 1,P2= x^3+ x^2 + 1。P1 + P2 = x^6+ x^5 + x^3+ x。即对应项想加减。
GF(2)的多项式乘除运算也与一般的多项式大体一样,只是加减时进行的是模2运算。不再详述,待会看下去就行。
CRC的数学基础就说到这里吧。再说下去只会让大家都懵了,我们还是换一些直白点的语言来描述下CRC原理。
在小学我们就知道,乘法可以通过一直加某个数来得到结果,同样除法也可以通过一直减某个数来得到结果。看下下面两个式子:
9/3=3 (余数是0),即9 – 3 – 3 –3 = 0
9/6 = 1 (余数是3),即9 – 6 = 3
用二进制来表示就是:
1001 -->9 0011 - -->3 ------------------------------------------------ 0110 -->6 0011 - -->3 ------------------------------------------------ 0011 -->3 0011 - -->3 ------------------------------------------------ 0000 -->余数
减了三次,显然商是3,而最后刚好减完,余数为0。
再来看下另外一个:
1001 -->9 0110 - -->6 ------------------------------------------------ 0011 -->3 , 余数
这次商是1,余数是3。
很容易吧。但上面的是有借位的,并不是我们之前说的2元素伽罗瓦域的减法。我们再来看看2元素伽罗瓦域的除法,也即CRC的运算。
如果忽略借位,那8/3 =?……?
1000 -->8 11 - -->3 ------------------------------------------------ 100 -->4 11 - -->3 ------------------------------------------------ 10 -->2 11 - -->3 ------------------------------------------------ 1 -->1 , 余数 ……The CRC
好奇怪,是吧,为什么从高位开始减呢?我们还原成除法就不奇怪了。
111 -->商
----------
11)1000
11
-------------------
100
11
--------------------
10
11
--------------------
1 -->余数,The CRC
普通的除法可以还原为熟悉的减法,但2元素伽罗瓦域的除法记得注意点了。从高位开始减。另外,余数得比除数的字长少,以二进制来准。不懂?11的字长是2,1的字长是1,这样懂了吧。而余数就是我们所关心的CRC。
进行一个CRC运算我们需要选择一个除数,这个除数我们叫它为“poly”(生成项),宽度W就是最高位的位置,所以我刚才举的例子中的除数3,这个poly 11的W是1,而不是2。注意最高位总是1,就像普通的数字小数点前面的0可以忽略一样。这里还要注意宽度与字长的区别,字长是从1开始计算的,而宽度是从0开始计算的。
现在我们再来看看改进后的CRC除法。
Poly = 1001,宽度W = 3
位串Bitstring = 11110
Bitstring + W zeroes = 11110 + 000 = 11110000
11110000
1001|||| -
-------------
1100|||
1001||| -
------------
1010||
1001|| -
-----------
0110|
0000| -
----------
1100
1001 -
---------
101 --> 5,余数 --> The CRC!
最后,还有两点要注意一下。咋这么多注意啊,别急,我们慢慢来。
1、只有当Bitstring的最高位为1,我们才将它与Poly进行XOR运算,否则我们只是将Bitstring左移一位。其实这很好理解,想下除法运算就明白了,这里只是用简单的减法来代替而已。
2、XOR运算的结果就是被操作位串Bitstring与Poly的低W位进行XOR运算,因为最高位总为0。
好了,以上就是CRC的原理了,晕了?那就再看一遍吧。其实也很好理解,也就一个XOR亦或运算。
明白了原理,我们还得讲它转化为程序的思想啊,我们用计算机的思维再来理下头绪看看。
我们假设待测数据是1101 0110 11,生成项Poly是10011,假设有一个4 bits的寄存器,通过反复的移位和进行CRC的除法,最终该寄存器中的值就是我们所要求的余数。
3 2 1 0 Bits
+---+---+---+---+
Pop <-- | | | | | <----- Augmented message(已加0扩张的原始数据)
+---+---+---+---+
1 0 0 1 1 = The Poly 生成项
依据这个模型,我们得到了一个最简单的算法:
1、把register中的值置0.
2、把原始的数据后添加w个0.
While (还有剩余没有处理的数据)
Begin
把register中的值左移一位,读入一个新的数据并置于register最低位的位置。
If (如果上一步的左移操作中的移出的一位是1)
register = register XOR Poly.
End
这里的Poly是10011,字长是5,位宽w是4,则生成最后的CRC的位宽也是4,所以,我们用一个4位的寄存器就可以了。另外,目标位串最高位如果是0的话,则是简单的移出去。真正参与运算的是1,而1 xor 1 = 0。所以我们可以将Poly最前面的1忽略,以及将Register移出的最高位忽略,因为这里的运算总是0。
唔~~,好像都解释一遍了吧,自己在脑海里面模拟下这个过程。还不懂的就回头再仔细看看,一些寄存器之类术语不懂的,我也不想解释了,百度一下吧。
下面看下完整的程序:
#include "StdAfx.h"
#include "stdio.h"
int main()
{
char POLY=0x13; //生成项Poly,0x13=10011b,这样CRC是4bit
unsigned short data = 0x035B; //待测数据是0x35B = 1101011011b,12bit,注意,数据不是16bit
unsigned short regi = 0x0000; //用0来填充寄存器的值,防止原先的垃圾值影响结果
//按CRC计算的定义,待测数据后加入4位 0,以容纳4bit的CRC;
//这样共有16bit待测数据,从第5bit开始做除法,就要做16-5+1=12次XOR
data <<= 4;
// 按二进制一位一位地开始计算
for ( int cur_bit = 15; cur_bit >= 0; -- cur_bit ) //处理16次,前4次实际上只是加载数据
{
//判断最高位是否为1
if ( ( ( regi >> 4 ) & 0x0001 ) == 0x1 ) regi = regi ^ POLY;
regi <<= 1; // 寄存器左移一位
// 读取目标位串下一位
unsigned short tmp = ( data >> cur_bit ) & 0x0001; //加载待测数据1bit到tmp中,tmp只有1bit
regi |= tmp; //这1bit加载到寄存器中
}
if ( ( ( regi >> 4 ) & 0x0001 ) == 0x1 ) regi = regi ^ POLY; //做最后一次XOR
//这时, regi中的值就是CRC
printf("0x%08X\n",regi);
return 0;
}
运行后打印出结果0x0000000E,也就是二进制的1110b,结果正确。
唔~~,原理说了,算法描述了,程序也给出来了。好像都完成了。其实不然,上面这个算法效率比较低,每次只能处理1bit,这速度得计算到什么时候啊,虽然计算机速度快,但也经不起耗啊,浪费资源,可耻。
那如何改进呢?如果我们能一次性运算一字节是不是就会快点了呢?显然的,但1 xor 1 =0,这很显然的,一字节怎么xor呢,一字节进行异或可以有256种结果,该怎么做好呢?我们可以先建立一张表,把这些结果都计算出来,然后放到这张表里面,为了方便索引,我们用寄存器移出的那一字节位串来进行索引。聪明的你会说,不对啊,结果还跟Poly生成项有关啊,毕竟xor是个二元运算。呵呵,Poly是一定的,我们只要根据我们程序使用的Poly来生成一个表就行了,或者事先在程序保存下来。在速度改进的同时,空间占用会大一点,不过这点空间相对来说还是可以忽略的。
显然,不同的生成项检错能力也不同,找到一个好的生成项需要具备比较好的数学基础。但不用担心,很多先驱已经为我们做好这件事。
以下是一些标准的CRC算法的生成多项式:
| 标准 |
生成多项式 |
16进制表示 |
| CRC12 |
x^12 + x^11 + x^3 + x^2 + x + 1 |
80F |
| CRC16 |
x^16 + x^15 + x^2 + 1 |
8005 |
| CRC16-CCITT |
x^16 + x^12 + x^5 + 1 |
1021 |
| CRC32 |
x^32 + x^26 + x^23 + x^22 + x^16 + x^12 + x^11+ x^10 + x^8 + x^7 + x^5 + x^4 + x^2 + x + 1 |
04C11DB7 |
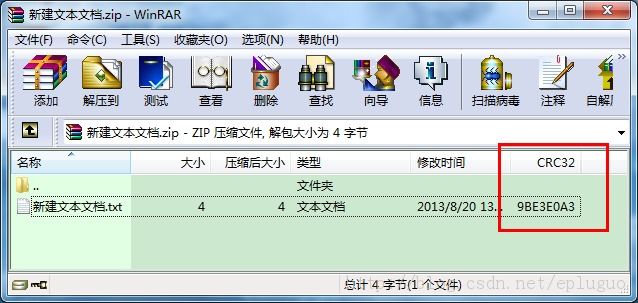
其实,这个索引表,网上很多的地方都不一样,很杂乱,很多人都是根据自己的理解来生成一个CRC表,这样也可以满足基本的校验需要。其实这个表有好几种,这里只介绍一种,正规查询表,也就是被正式引用的一种。Winrar对生成的压缩包里面的每个文件都有一个CRC32校验值,那就是用正规查询表来生成的。但还不止这样,还有各种颠倒(reflect)啊之类的,其实正规查询表本身就是经过反射(reflect)的,有兴趣的再下载附件里面的资料来看看。这里只给出实现。
先看看CRC32的正规查询表吧
unsigned LONG CRC32Table[256] = {
0x00000000,0x77073096,0xEE0E612C,0x990951BA,0x076DC419,0x706AF48F,0xE963A535,0x9E6495A3,
0x0EDB8832,0x79DCB8A4,0xE0D5E91E,0x97D2D988,0x09B64C2B,0x7EB17CBD,0xE7B82D07,0x90BF1D91,
0x1DB71064,0x6AB020F2,0xF3B97148,0x84BE41DE,0x1ADAD47D,0x6DDDE4EB,0xF4D4B551,0x83D385C7,
0x136C9856,0x646BA8C0,0xFD62F97A,0x8A65C9EC,0x14015C4F,0x63066CD9,0xFA0F3D63,0x8D080DF5,
0x3B6E20C8,0x4C69105E,0xD56041E4,0xA2677172,0x3C03E4D1,0x4B04D447,0xD20D85FD,0xA50AB56B,
0x35B5A8FA,0x42B2986C,0xDBBBC9D6,0xACBCF940,0x32D86CE3,0x45DF5C75,0xDCD60DCF,0xABD13D59,
0x26D930AC,0x51DE003A,0xC8D75180,0xBFD06116,0x21B4F4B5,0x56B3C423,0xCFBA9599,0xB8BDA50F,
0x2802B89E,0x5F058808,0xC60CD9B2,0xB10BE924,0x2F6F7C87,0x58684C11,0xC1611DAB,0xB6662D3D,
0x76DC4190,0x01DB7106,0x98D220BC,0xEFD5102A,0x71B18589,0x06B6B51F,0x9FBFE4A5,0xE8B8D433,
0x7807C9A2,0x0F00F934,0x9609A88E,0xE10E9818,0x7F6A0DBB,0x086D3D2D,0x91646C97,0xE6635C01,
0x6B6B51F4,0x1C6C6162,0x856530D8,0xF262004E,0x6C0695ED,0x1B01A57B,0x8208F4C1,0xF50FC457,
0x65B0D9C6,0x12B7E950,0x8BBEB8EA,0xFCB9887C,0x62DD1DDF,0x15DA2D49,0x8CD37CF3,0xFBD44C65,
0x4DB26158,0x3AB551CE,0xA3BC0074,0xD4BB30E2,0x4ADFA541,0x3DD895D7,0xA4D1C46D,0xD3D6F4FB,
0x4369E96A,0x346ED9FC,0xAD678846,0xDA60B8D0,0x44042D73,0x33031DE5,0xAA0A4C5F,0xDD0D7CC9,
0x5005713C,0x270241AA,0xBE0B1010,0xC90C2086,0x5768B525,0x206F85B3,0xB966D409,0xCE61E49F,
0x5EDEF90E,0x29D9C998,0xB0D09822,0xC7D7A8B4,0x59B33D17,0x2EB40D81,0xB7BD5C3B,0xC0BA6CAD,
0xEDB88320,0x9ABFB3B6,0x03B6E20C,0x74B1D29A,0xEAD54739,0x9DD277AF,0x04DB2615,0x73DC1683,
0xE3630B12,0x94643B84,0x0D6D6A3E,0x7A6A5AA8,0xE40ECF0B,0x9309FF9D,0x0A00AE27,0x7D079EB1,
0xF00F9344,0x8708A3D2,0x1E01F268,0x6906C2FE,0xF762575D,0x806567CB,0x196C3671,0x6E6B06E7,
0xFED41B76,0x89D32BE0,0x10DA7A5A,0x67DD4ACC,0xF9B9DF6F,0x8EBEEFF9,0x17B7BE43,0x60B08ED5,
0xD6D6A3E8,0xA1D1937E,0x38D8C2C4,0x4FDFF252,0xD1BB67F1,0xA6BC5767,0x3FB506DD,0x48B2364B,
0xD80D2BDA,0xAF0A1B4C,0x36034AF6,0x41047A60,0xDF60EFC3,0xA867DF55,0x316E8EEF,0x4669BE79,
0xCB61B38C,0xBC66831A,0x256FD2A0,0x5268E236,0xCC0C7795,0xBB0B4703,0x220216B9,0x5505262F,
0xC5BA3BBE,0xB2BD0B28,0x2BB45A92,0x5CB36A04,0xC2D7FFA7,0xB5D0CF31,0x2CD99E8B,0x5BDEAE1D,
0x9B64C2B0,0xEC63F226,0x756AA39C,0x026D930A,0x9C0906A9,0xEB0E363F,0x72076785,0x05005713,
0x95BF4A82,0xE2B87A14,0x7BB12BAE,0x0CB61B38,0x92D28E9B,0xE5D5BE0D,0x7CDCEFB7,0x0BDBDF21,
0x86D3D2D4,0xF1D4E242,0x68DDB3F8,0x1FDA836E,0x81BE16CD,0xF6B9265B,0x6FB077E1,0x18B74777,
0x88085AE6,0xFF0F6A70,0x66063BCA,0x11010B5C,0x8F659EFF,0xF862AE69,0x616BFFD3,0x166CCF45,
0xA00AE278,0xD70DD2EE,0x4E048354,0x3903B3C2,0xA7672661,0xD06016F7,0x4969474D,0x3E6E77DB,
0xAED16A4A,0xD9D65ADC,0x40DF0B66,0x37D83BF0,0xA9BCAE53,0xDEBB9EC5,0x47B2CF7F,0x30B5FFE9,
0xBDBDF21C,0xCABAC28A,0x53B39330,0x24B4A3A6,0xBAD03605,0xCDD70693,0x54DE5729,0x23D967BF,
0xB3667A2E,0xC4614AB8,0x5D681B02,0x2A6F2B94,0xB40BBE37,0xC30C8EA1,0x5A05DF1B,0x2D02EF8D
};
这个表其实可以在程序里生成,下面给出的完整代码就是在程序里面生成的。
#include "StdAfx.h"
#include "stdio.h"
//颠倒字串的顺序
unsigned long int Reflect(unsigned long int ulReflect, int nBitCount)
{
unsigned long int value=0;
// 交换bit0和bit7,bit1和bit6,类推
for(int i = 1; i < (nBitCount + 1); i++)
{
if(ulReflect & 1)
value |= 1 << (nBitCount - i);
ulReflect >>= 1;
}
return value;
}
unsigned long CRC32(void * DataBuf,unsigned long ulLen)
{
unsigned long int crc,temp;
unsigned long int ulPolynomial = 0x04c11db7; //标准的CRC32生成项
static unsigned long int crc32_table[256] = {0};
static int IsDoTable = 0;
//检查是否已生成正规查询表
if (0 == IsDoTable)
{
for(int i = 0; i <= 0xFF; i++) // 生成CRC32“正规查询表”
{
temp=Reflect(i, 8);
crc32_table[i]= temp<< 24;
for (int j = 0; j < 8; j++)
{
unsigned long int t1,t2;
unsigned long int flag=crc32_table[i]&0x80000000;
t1=(crc32_table[i] << 1);
if(flag==0)
t2=0;
else
t2=ulPolynomial;
crc32_table[i] =t1^t2 ;
}
crc=crc32_table[i];
crc32_table[i] = Reflect(crc32_table[i], 32);
}
IsDoTable = 1;
}
//计算CRC32值
unsigned long lRes;
unsigned long ii;
unsigned long m_CRC = 0xFFFFFFFF; //寄存器中预置初始值
char *p = (char *)DataBuf;
for(ii=0; ii <ulLen; ii++)
{
m_CRC = crc32_table[( m_CRC^(*(p+ii)) ) & 0xff] ^ (m_CRC >> 8); //计算
}
lRes= ~m_CRC; //取反
return lRes;
}
int main()
{
char DataBuf[512]={0x31,0x32,0x33,0x34}; //待测数据,为Ascii字符串"1234"
printf("0x%08X\n",CRC32(DataBuf,4));
return 0;
}
下面是结果:
学了两天CRC了,这只是一些总结。包括基本的原理及最终优化实现,但更深一层的优化算法没有细说,如果有读者想要继续了解更深一层的优化,可以下载附件来看看,在此再次感谢附件的作者。
忘了CSDN的附件是单独管理的,这里给出个资源链接吧:http://download.csdn.net/detail/epluguo/5980501
关于CRC的更多资料,而已参阅wiki百科:http://zh.wikipedia.org/zh-cn/%E5%BE%AA%E7%8E%AF%E5%86%97%E4%BD%99%E6%A0%A1%E9%AA%8C