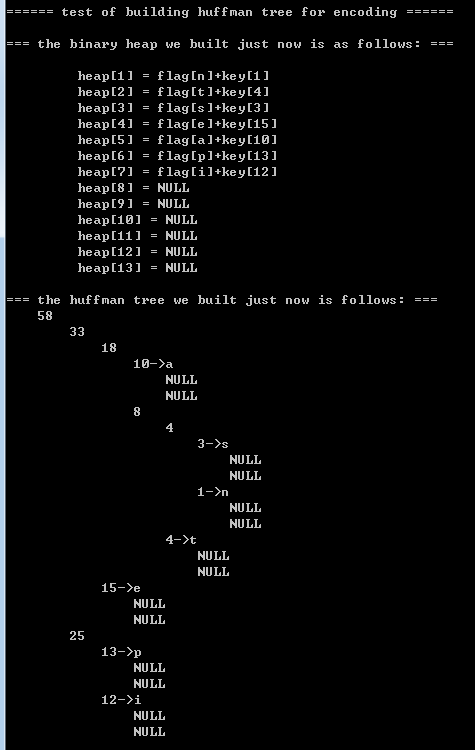
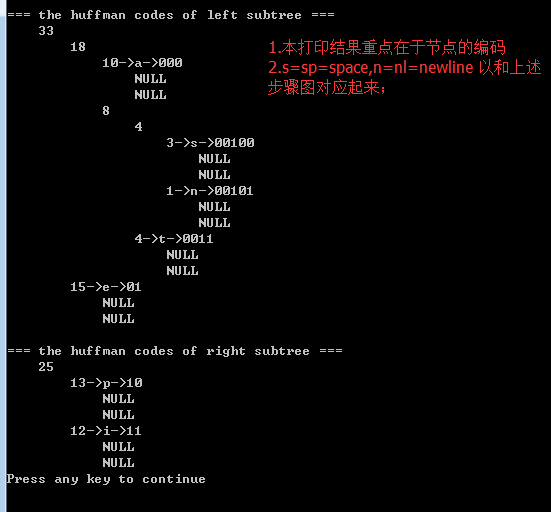
Huffman编码（Huffman树）

【0】README

0.1） 本文总结于 数据结构与算法分析， 源代码均为原创， 旨在 理解 “Huffman编码（Huffman树）” 的idea 并用源代码加以实现；
0.2） Huffman树的构建算法属于 贪婪算法， 贪婪算法的基础知识参见： 　http://blog.csdn.net/pacosonswjtu/article/details/50071159

【1】Huffman 编码

1.1）贪婪算法的第二个应用： 文件压缩；

• 1.1.1）标准的 ASCII字符集： 它由大约100个 可打印字符组成，为了把这些字符区分开， 需要 |log100|（不小于等于log100） = 7个 比特；

• 1.1.2）看个荔枝：（使用一个标准编码方案）
  设一个文件， 它只包含字符 a, e, i, s, t, 加上一些空格和 newline（换行）。 进一步设该文件有10个a、15个e、12个i、3个s、4个t、13个空格以及一个 newline， 如图10-8所示， 这个文件需要174个bits 来表示，因为有58个字符，每个字符3个bits；
  
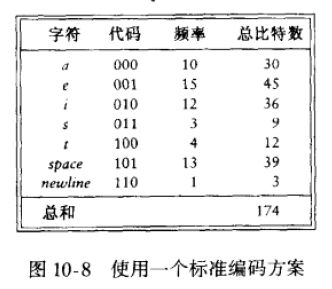
  1.2）现实中的事实： 文件可能相当大。 许多大文件是某个程序的输出数据，而在使用频率最大和最小之间的字符间通常存在很大的差别；

• 1.2.1）出现的问题：是否有可能提供一种更好的编码降低总的所需bits数量

2.2）解决方法：一般策略就是让代码的长度从字符到字符是编号不等的，　同时保证经常出现的字符其代码短；（注意，　如果所有的字符都以相同的频率出现，　那么要节省空间是不可能的）
2.３）代表字母的二进制代码用二叉树来表示：

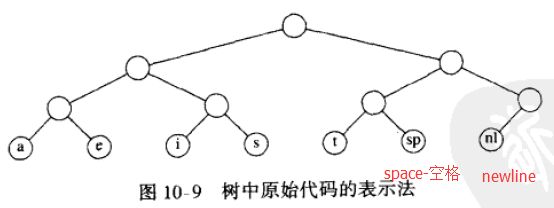
对上图的分析（Analysis）：

• A1）上图中的树只在树叶上有数据。 每个字符通过从根节点开始用0指示 左分支用1指示右分支 而以记录路径的方法表示出来。如， s通过从根向左走， 然后向右， 最后再向右而达到， 于是它被编码为 011。这种数据结构叫做 trie树；（trie==单词查找树）
• A2）如果字符 ci 在深度 di 处并且出现 fi次， 那么该字符编码的值就等于 ∑di * fi；
• A3）因为 newline（nl）是仅有的一个儿子，我们把它放到它的更高一层的父节点上， 如下图所示：
  
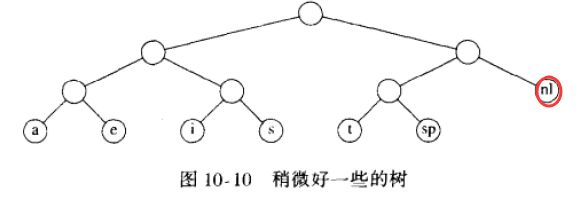
• A4）上图中的树是满树（full tree）：所有的节点或者是树叶，或者有两个儿子；

1.4）综上所述： 我们看到，基本的问题在于找到总价值最小的满二叉树，其中所有的字符都位于树叶上， 下图显示了简单字母表的最优树：

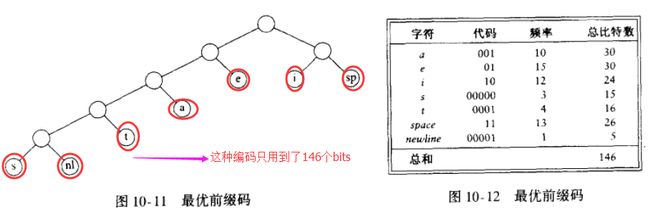
• 1.4.1）那么问题来了：如何构造编码树；
• 1.4.2）解决方法（引入哈夫曼编码）： 1952年 Huffman 给出了一个算法， 因此，这种编码系统通常称为 哈夫曼编码（Huffman code）；

【2】哈夫曼算法

2.1）算法描述：
算法对一个由树组成的森林 进行。一棵树的权等于它的树叶的频率的和。任意选取最小权的两颗树T1 和 T2， 并任意形成以 T1 和 T2 为子树的新树， 将这样的过程进行 C-1 次。在算法的开始， 存在C 颗单节点树——每个字符一颗。在算法结束时得到一颗树， 这颗树就是最优哈夫曼编码树了；
2.2）看个荔枝（构建哈夫曼编码树的steps）：

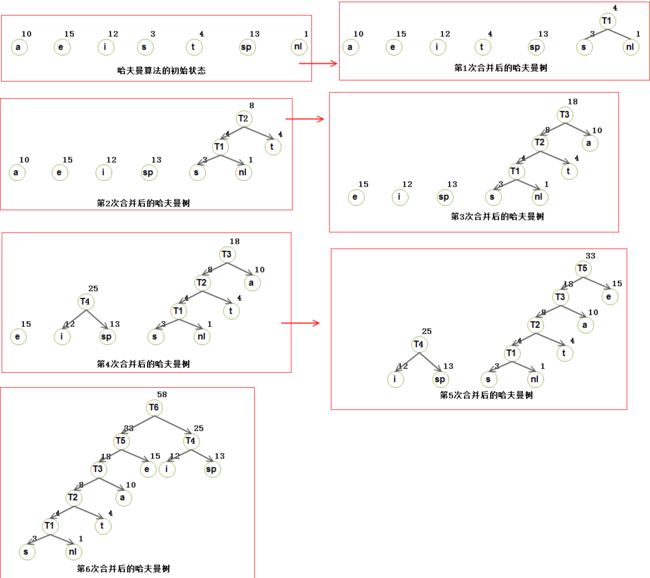
2.3）下面，我们验证哈夫曼算法产生最优代码的证明思路：

• step1）首先 ，由反证法证明树是满的， 因为我们已经看到一颗不满的树是改进进成满树的；
• step2）其次，我们必须证明两个频率最小的字符 α和β必然是两个最深的节点；
• step3）然后，我们再证明， 在相同深度上任意两个节点处的字符可以交换而不影响最优性；这说明， 总可以找到一颗树， 它含有两个最不经常出现的符号作为兄弟；

2.4）该算法是贪婪算法的原因在于： 在每一阶段我们都进行一次合并而没有进行全局的考虑， 我们只是选择两颗最小的树；
2.5） 如何实现？

• method1）如果我们依权排序将这些树保存在一个优先队列中， 那么， 由于对元素个数不超过C的优先队列将进行一次 buildHeap ， 2C -2 次 deleteMin 和 C-2 次insert， 故运行时间为 O（ClogC）。
• method2）使用一个链表简单实现该队列将给出一个O（C^2）算法；
• Conclusion） 优先队列实现方法的选择取决于C有多大： 在ASCII 字符集下，C是足够小的， 这使得二次运行时间是可以接收的。 在这样的应用中， 实际上几乎所有的运行时间都将花费在读入输入文件和写出压缩文件所需要的磁盘I/O 操作上；

2.6）有两个细节要考虑（details）

• d1）第一个问题是： 首先， 在压缩文件的开头必须传送编码信息，因为否则将不可能译码；对于一些小文件，传送编码信息表的代价将超过压缩带来的任何可能的节省， 最后的结果很可能是文件扩大。 当然，这可以检测到且原文件可以原样保留； 而对于大型文件， 信息表的大小是无关紧要的；
• d2）第二个问题是： 该算法是一个两趟扫描算法。 第一遍搜集频率数据， 第二遍进行编码。显然， 对于处理大型文件的程序来说，这个性质不是我们所需要的；

【3】source code + printing results

3.1）download source code： https://github.com/pacosonTang/dataStructure-algorithmAnalysis/tree/master/chapter10/p266_huffman
3.2）source code at a glance：（for complete code , please click the given link above）

1st func: building huffman tree

// building huffman tree 
void buildHuffman()
{    
    ElementTypePtr temp;        
    char* codes;
    int off;

    off = 0;
    codes = buildCharArray(off+1);
    temp = buildElement();  

    initElement(temp);
    while(!isEmpty(bh))
    {   
        insertHeap(*temp, bh);      
        initElement(temp);
    }   
    temp->code = '\0';

    printf("\n=== the huffman tree we built just now is follows: ===\n");
    printHuffmanTree(temp, 1);
    printf("\n=== the huffman codes of left subtree ===\n");
    printHuffmanCode(temp->left, 1, off, codes);
    printf("\n=== the huffman codes of right subtree ===\n");
    printHuffmanCode(temp->right, 1, off, codes);
}

2nd func: print huffman tree node

void copyCharArray(char *a, char *b, int size)
{
    int i;

    for(i=0; i<=size; i++)
        a[i] = b[i];
}

void printHuffmanTree(ElementTypePtr root, int depth)
{        
    int i;

    if(root) 
    {               
        for(i = 0; i < depth; i++)
            printf(" ");             
        if(root->left!=NULL)        
            printf("%d\n", root->key);      
        else
            printf("%d->%c\n", root->key, root->flag);

        printHuffmanTree(root->left,depth+1); 
        printHuffmanTree(root->right, depth+1); // Attention: there's difference between traversing binary tree and common tree 
    }
    else 
    {
        for(i = 0; i < depth; i++)
            printf(" ");     
        printf("NULL\n");
    }
}

3rd func: print huffman code of every node

void printHuffmanCode(ElementTypePtr root, int depth, int off, char *codes)
{   
    int i;  
    char *innerCode = buildCharArray(off+2); 
        
    copyCharArray(innerCode, codes, off);
    if(root) 
    {   
        innerCode[off] = root->code;
        innerCode[++off] = '\0';            

        for(i = 0; i < depth; i++)
            printf(" ");     
        
        if(root->left!=NULL)        
            printf("%d\n", root->key);      
        else
            printf("%d->%c->%s\n", root->key, root->flag, innerCode);

        printHuffmanCode(root->left,depth+1, off, innerCode); 
        printHuffmanCode(root->right, depth+1, off, innerCode); // Attention: there's difference between traversing binary tree and common tree 
    }
    else 
    {
        for(i = 0; i < depth; i++)
            printf(" ");     
        printf("NULL\n");
    }
}

3.3）printing results：