《利用python进行数据分析》读书笔记--第十一章 金融和经济数据应用（一）

自2005年开始，python在金融行业中的应用越来越多，这主要得益于越来越成熟的函数库（NumPy和pandas）以及大量经验丰富的程序员。许多机构发现python不仅非常适合成为交互式的分析环境，也非常适合开发文件的系统，所需的时间也比Java或C++少得多。Python还是一种非常好的粘合层，可以非常轻松为C或C++编写的库构建Python接口。

金融分析领域的内容博大精深。在数据规整化方面所花费的精力常常会比解决核心建模和研究问题所花费的时间多得多。

在本章中，术语截面（cross-section）来表示某个时间点的数据。例如标普500指数中所有成份股在特定日期的收盘价就形成了一个截面。多个数据在多个时间点的截面数据就构成了一个面板（panel）。面板数据既可以表示为层次化索引的DataFrame，也可以表示为三维的Panel pandas对象。

1、数据规整化方面的话题

时间序列以及截面对齐

处理金融数据时，最费神的一个问题就是所谓的数据对齐（data alignment）。两个时间序列的索引可能没有很好的对齐，或者两个DataFrame对象可能含有不匹配的行或者列。MATLAB、R用户通常会耗费大量的时间来进行数据对对齐工作（确实如此）。

pandas可以在运算中自动对齐数据。这是极好的，会提高效率。

• 时间序列以及截面对齐

#-*- coding:utf-8 -*-
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import datetime as dt
from pandas import Series,DataFrame
from datetime import datetime
from dateutil.parser import parse
import time

prices = pd.read_csv('E:\\stock_px.csv',parse_dates = True,index_col = 0)
volume = pd.read_csv('E:\\volume.csv',parse_dates = True,index_col = 0)
prices = prices.ix['2011-09-06':'2011-09-14',['AAPL','JNJ','SPX','XOM']]
volume = volume.ix['2011-09-06':'2011-09-12',['AAPL','JNJ','XOM']]
print prices
print volume,'\n'
#如果想计算一个基于成交量的加权平均价，只需要做下面的事即可
vwap = (prices * volume).sum() / volume.sum()  #sum函数自动忽略NaN值
print vwap,'\n'
print vwap.dropna(),'\n'
#可以使用DataFrame的align方法将DataFrame显示地对齐
print prices.align(volume,join = 'inner')
#另一个不可或缺的功能是，通过一组索引可能不同的Series构建DataFrame
s1 = Series(range(3),index = ['a','b','c'])
s2 = Series(range(4),index = ['d','b','c','e'])
s3 = Series(range(3),index = ['f','a','c'])
data = DataFrame({'one':s1,'two':s2,'three':s3})
print data
>>>
              AAPL    JNJ      SPX    XOM
2011-09-06  379.74  64.64  1165.24  71.15
2011-09-07  383.93  65.43  1198.62  73.65
2011-09-08  384.14  64.95  1185.90  72.82
2011-09-09  377.48  63.64  1154.23  71.01
2011-09-12  379.94  63.59  1162.27  71.84
2011-09-13  384.62  63.61  1172.87  71.65
2011-09-14  389.30  63.73  1188.68  72.64
                AAPL       JNJ       XOM
2011-09-06  18173500  15848300  25416300
2011-09-07  12492000  10759700  23108400
2011-09-08  14839800  15551500  22434800
2011-09-09  20171900  17008200  27969100
2011-09-12  16697300  13448200  26205800 

AAPL    380.655181
JNJ      64.394769
SPX            NaN
XOM      72.024288 

AAPL    380.655181
JNJ      64.394769
XOM      72.024288 

(              AAPL    JNJ    XOM
2011-09-06  379.74  64.64  71.15
2011-09-07  383.93  65.43  73.65
2011-09-08  384.14  64.95  72.82
2011-09-09  377.48  63.64  71.01
2011-09-12  379.94  63.59  71.84,                 AAPL       JNJ       XOM
2011-09-06  18173500  15848300  25416300
2011-09-07  12492000  10759700  23108400
2011-09-08  14839800  15551500  22434800
2011-09-09  20171900  17008200  27969100
2011-09-12  16697300  13448200  26205800)
   one  three  two
a    0      1  NaN
b    1    NaN    1
c    2      2    2
d  NaN    NaN    0
e  NaN    NaN    3
f  NaN      0  NaN
[Finished in 2.8s]

• 频率不同的时间按序列的运算

经济学时间序列常常按年月日等频率进行数据统计。

#-*- coding:utf-8 -*-
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import datetime as dt
from pandas import Series,DataFrame
from datetime import datetime
from dateutil.parser import parse
import time

ts1 = Series(np.random.randn(3),index = pd.date_range('2012-6-13',periods = 3,freq = 'W-WED'))
print ts1
#如果重采样到工作日，就会有缺省值出现
print ts1.resample('B')
print ts1.resample('B',fill_method = 'ffill'),'\n'
#下面看一种不规则时间的序列
dates = pd.DatetimeIndex(['2012-6-12','2012-6-17','2012-6-18','2012-6-21','2012-6-22','2012-6-29'])
ts2 = Series(np.random.randn(6),index = dates)
print ts2,'\n'
#如果想将处理过后的ts1加到ts2上，可以先将两个频率弄相同再相加，但是要想维持ts2的reindex，则用reindex就好
print ts1.reindex(ts2.index,method = 'ffill'),'\n'
print ts2 + ts1.reindex(ts2.index,method = 'ffill'),'\n'
>>>
2012-06-13   -0.855102
2012-06-20   -1.242206
2012-06-27    0.380710
Freq: W-WED
2012-06-13   -0.855102
2012-06-14         NaN
2012-06-15         NaN
2012-06-18         NaN
2012-06-19         NaN
2012-06-20   -1.242206
2012-06-21         NaN
2012-06-22         NaN
2012-06-25         NaN
2012-06-26         NaN
2012-06-27    0.380710
Freq: B
2012-06-13   -0.855102
2012-06-14   -0.855102
2012-06-15   -0.855102
2012-06-18   -0.855102
2012-06-19   -0.855102
2012-06-20   -1.242206
2012-06-21   -1.242206
2012-06-22   -1.242206
2012-06-25   -1.242206
2012-06-26   -1.242206
2012-06-27    0.380710
Freq: B 

2012-06-12   -1.248346
2012-06-17    0.833907
2012-06-18    0.235492
2012-06-21   -1.172378
2012-06-22   -0.111804
2012-06-29   -0.458527 

2012-06-12         NaN
2012-06-17   -0.855102
2012-06-18   -0.855102
2012-06-21   -1.242206
2012-06-22   -1.242206
2012-06-29    0.380710
2012-06-12         NaN
2012-06-17   -0.021195
2012-06-18   -0.619610
2012-06-21   -2.414584
2012-06-22   -1.354010
2012-06-29   -0.077817 

[Finished in 1.7s]

• 使用Period

Period是一种好工具，尤其适合于处理特殊规范的以年或者季度为频率的金融或经济序列。比如，一个公司可能会发布其以6月结尾的财年的每季度盈利报告，即频率为Q-JUN。来看两个例子：

#-*- coding:utf-8 -*-
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import datetime as dt
from pandas import Series,DataFrame
from datetime import datetime
from dateutil.parser import parse
import time

gdp = Series([1.78,1.94,2.08,2.01,2.15,2.31,2.46],index = pd.period_range('1984Q2',periods = 7,freq = 'Q-SEP'))
print gdp,'\n'
infl = Series([0.025,0.045,0.037,0.04],index = pd.period_range('1982',periods = 4,freq = 'A-DEC'))
print infl,'\n'
#跟Timestamp时间序列不同的是，由period索引的不同时间序列之间的转换必须经过显示转换
#转换为以九月份为一年结束，以季度为频率的序列，end就是说：这一年里面最后一个季度的名字
infl_q = infl.asfreq('Q-SEP',how = 'end')
print infl.asfreq('Q-SEP',how = 'start'),'\n' #看一下以start开头
print infl_q,'\n'
#显示转换为以后就可以被重新索引了
print infl_q.reindex(gdp.index,method = 'ffill')
>>>
1984Q2    1.78
1984Q3    1.94
1984Q4    2.08
1985Q1    2.01
1985Q2    2.15
1985Q3    2.31
1985Q4    2.46
Freq: Q-SEP 

1982    0.025
1983    0.045
1984    0.037
1985    0.040
Freq: A-DEC 

1982Q2    0.025
1983Q2    0.045
1984Q2    0.037
1985Q2    0.040
Freq: Q-SEP 

1983Q1    0.025
1984Q1    0.045
1985Q1    0.037
1986Q1    0.040
Freq: Q-SEP 

1984Q2    0.045
1984Q3    0.045
1984Q4    0.045
1985Q1    0.037
1985Q2    0.037
1985Q3    0.037
1985Q4    0.037
Freq: Q-SEP
[Finished in 1.4s]

• 时间和“最当前”数据选取

#-*- coding:utf-8 -*-
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import datetime as dt
from pandas import Series,DataFrame
from datetime import datetime
from dateutil.parser import parse
from datetime import time

#假设有一个很长的盘中数据，现在希望抽取其中的一些，如果数据不规整该怎么办？
rng = pd.date_range('2012-06-01 09:30','2012-06-01 15:59',freq = 'T')
print type(rng)  #这种类型可以append
#注意下面的组做法，通过时间的偏移得到更多数据
rng = rng.append([rng + pd.offsets.BDay(i) for i in range(1,4)])
print rng,'\n'
ts = Series(np.arange(len(rng),dtype = float),index = rng)
print ts,'\n'  
print time(10,0)  #这就是10点
print ts[time(10,0)],'\n'   #只取10点钟的数据
#该操作实际上用了实例方法at_time（各时间序列以及类似的DataFrame对象都有）
print ts.at_time(time(10,0)),'\n'
#当然还会有between_time来选取两个Time对象之间的值
print ts.between_time(time(10,0),time(10,1)),'\n'
#可是可能刚好就没有任何数据落在某个具体的时间上（比如上午10点）。这时，可能会希望得到上午10点之前最后出现的值
#下面将该时间序列的大部分内容随机设置为NA
indexer = np.sort(np.random.permutation(len(ts))[700:])
irr_ts = ts.copy()
irr_ts[indexer] = np.nan
print irr_ts['2012-06-01 09:50':'2012-06-01 10:00'],'\n'
#如果将一组Timestamp传入asof方法，就能得到这些时间点处（或其之前最近）的有效值（非NA）。例如，构造一个日期范围（每天上午10点），然后将其传入asof：
selection = pd.date_range('2012-06-01 10:00',periods = 4,freq = 'B')
print irr_ts.asof(selection)
>>>
<class 'pandas.tseries.index.DatetimeIndex'>
<class 'pandas.tseries.index.DatetimeIndex'>
[2012-06-01 09:30:00, ..., 2012-06-06 15:59:00]
Length: 1560, Freq: None, Timezone: None 

2012-06-01 09:30:00     0
2012-06-01 09:31:00     1
2012-06-01 09:32:00     2
2012-06-01 09:33:00     3
2012-06-01 09:34:00     4
2012-06-01 09:35:00     5
2012-06-01 09:36:00     6
2012-06-01 09:37:00     7
2012-06-01 09:38:00     8
2012-06-01 09:39:00     9
2012-06-01 09:40:00    10
2012-06-01 09:41:00    11
2012-06-01 09:42:00    12
2012-06-01 09:43:00    13
2012-06-01 09:44:00    14
...
2012-06-06 15:45:00    1545
2012-06-06 15:46:00    1546
2012-06-06 15:47:00    1547
2012-06-06 15:48:00    1548
2012-06-06 15:49:00    1549
2012-06-06 15:50:00    1550
2012-06-06 15:51:00    1551
2012-06-06 15:52:00    1552
2012-06-06 15:53:00    1553
2012-06-06 15:54:00    1554
2012-06-06 15:55:00    1555
2012-06-06 15:56:00    1556
2012-06-06 15:57:00    1557
2012-06-06 15:58:00    1558
2012-06-06 15:59:00    1559
Length: 1560 

10:00:00
2012-06-01 10:00:00      30
2012-06-04 10:00:00     420
2012-06-05 10:00:00     810
2012-06-06 10:00:00    1200 

2012-06-01 10:00:00      30
2012-06-04 10:00:00     420
2012-06-05 10:00:00     810
2012-06-06 10:00:00    1200 

2012-06-01 10:00:00      30
2012-06-01 10:01:00      31
2012-06-04 10:00:00     420
2012-06-04 10:01:00     421
2012-06-05 10:00:00     810
2012-06-05 10:01:00     811
2012-06-06 10:00:00    1200
2012-06-06 10:01:00    1201 

2012-06-01 09:50:00    20
2012-06-01 09:51:00    21
2012-06-01 09:52:00    22
2012-06-01 09:53:00   NaN
2012-06-01 09:54:00    24
2012-06-01 09:55:00    25
2012-06-01 09:56:00    26
2012-06-01 09:57:00    27
2012-06-01 09:58:00   NaN
2012-06-01 09:59:00    29
2012-06-01 10:00:00    30 

2012-06-01 10:00:00      30
2012-06-04 10:00:00     419
2012-06-05 10:00:00     810
2012-06-06 10:00:00    1199
Freq: B
[Finished in 1.2s]

• 拼接多个数据源

在第七章中曾经介绍了数据拼接的知识，在金融或经济中，还有另外几个经常出现的情况：

1. 在一个特定的时间点上，从一个数据源切换到另一个数据源
2. 用另一个时间序列对当前时间序列中的缺失值“打补丁”
3. 将数据中的符号（国家、资产代码等）替换为实际数据

#-*- coding:utf-8 -*-
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import datetime as dt
from pandas import Series,DataFrame
from datetime import datetime
from dateutil.parser import parse
from datetime import time

#关于特定时间的数据源切换，就是用concat函数进行连接
data1 = DataFrame(np.ones((6,3),dtype = float),columns = ['a','b','c'],index = pd.date_range('6/12/2012',periods = 6))
data2 = DataFrame(np.ones((6,3),dtype = float)*2,columns = ['a','b','c'],index = pd.date_range('6/13/2012',periods = 6))
print data1
print data2,'\n'
spliced = pd.concat([data1.ix[:'2012-06-14'],data2.ix['2012-06-15':]])
print spliced,'\n'
#假设data1缺失了data2中存在的某个时间序列
data2 = DataFrame(np.ones((6,4),dtype = float)*2,columns = ['a','b','c','d'],index = pd.date_range('6/13/2012',periods = 6))
spliced = pd.concat([data1.ix[:'2012-06-14'],data2.ix['2012-06-15':]])
print spliced,'\n'
#combine_first可以引入合并点之前的数据，这样也就扩展了'd'项的历史
spliced_filled = spliced.combine_first(data2)
print spliced_filled,'\n' 
#DataFrame也有一个类似的方法update，它可以实现就地更新，如果只想填充空洞，则必须差U纳入overwrite = False才行
#不传入overwrite会把整条数据都覆盖
spliced.update(data2,overwrite = False)
print spliced,'\n'
#上面所讲的技术可以将数据中的符号替换为实际数据，但有时利用 DataFrame的索引机制直接进行设置会更简单一些
cp_spliced = spliced.copy()
cp_spliced[['a','c']] = data1[['a','c']]
print cp_spliced
>>>
            a  b  c
2012-06-12  1  1  1
2012-06-13  1  1  1
2012-06-14  1  1  1
2012-06-15  1  1  1
2012-06-16  1  1  1
2012-06-17  1  1  1
            a  b  c
2012-06-13  2  2  2
2012-06-14  2  2  2
2012-06-15  2  2  2
2012-06-16  2  2  2
2012-06-17  2  2  2
2012-06-18  2  2  2 

            a  b  c
2012-06-12  1  1  1
2012-06-13  1  1  1
2012-06-14  1  1  1
2012-06-15  2  2  2
2012-06-16  2  2  2
2012-06-17  2  2  2
2012-06-18  2  2  2 

            a  b  c   d
2012-06-12  1  1  1 NaN
2012-06-13  1  1  1 NaN
2012-06-14  1  1  1 NaN
2012-06-15  2  2  2   2
2012-06-16  2  2  2   2
2012-06-17  2  2  2   2
2012-06-18  2  2  2   2 

            a  b  c   d
2012-06-12  1  1  1 NaN
2012-06-13  1  1  1   2
2012-06-14  1  1  1   2
2012-06-15  2  2  2   2
2012-06-16  2  2  2   2
2012-06-17  2  2  2   2
2012-06-18  2  2  2   2 

            a  b  c   d
2012-06-12  1  1  1 NaN
2012-06-13  1  1  1   2
2012-06-14  1  1  1   2
2012-06-15  2  2  2   2
2012-06-16  2  2  2   2
2012-06-17  2  2  2   2
2012-06-18  2  2  2   2 

             a  b   c   d
2012-06-12   1  1   1 NaN
2012-06-13   1  1   1   2
2012-06-14   1  1   1   2
2012-06-15   1  2   1   2
2012-06-16   1  2   1   2
2012-06-17   1  2   1   2
2012-06-18 NaN  2 NaN   2
[Finished in 1.4s]

• 收益指数和累计收益

金融领域中，收益（return）通常指的是某资产价格的百分比变化。

#-*- coding:utf-8 -*-
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import datetime as dt
from pandas import Series,DataFrame
from datetime import datetime
from dateutil.parser import parse
from datetime import time
import pandas.io.data as web

#下面是2011到2012年检贫国公公司的股票价格数据
price = web.get_data_yahoo('AAPL','2011-01-01')['Adj Close']
print price[-5:]
#对于苹果公司的股票(当时无股息)，计算两个时间点之间的累计百分比回报只需计算价格的百分比变化即可
print price['2011-10-03'] / price['2011-3-01'] - 1,'\n'
#对于其他那些派发股息的股票，要计算赚了（或者赔了……）多少钱就比较复杂了，不过这里所使用的已调整收盘价已经对拆分和股息做出了调整
#不管怎么样，通常会先算出一个收益指数，它表示单位投资（比如1美元）收益的时间序列
#从收益指数中可以得出许多假设。例如，人们可以决定是否进行利润再投资
#可以用cumprod计算出一个简单的收益指数
returns = price.pct_change()
ret_index = (1 + returns).cumprod()
ret_index[0] = 1
print ret_index,'\n'
#得到收益指数之后，计算指定时期内的累计收益就很简单了
m_returns = ret_index.resample('BM',how = 'last').pct_change()
print m_returns['2012']
#当然了，就这个简单的例子而言（没有股息也没有考虑其他调整），上面的结果也能通过重采样聚合（这里的聚合为时期）从日百分比变化中计算得出
m_rets = (1 + returns).resample('M',how = 'prod',kind = 'period') - 1
print m_rets['2012']
#如果知道了股息的派发日和支付率，就可以将它们计入到每日总收益中
returns[dividend_dates] += dividend_pcts
>>>
Date
2015-12-14    112.480003
2015-12-15    110.489998
2015-12-16    111.339996
2015-12-17    108.980003
2015-12-18    106.029999
Name: Adj Close
0.0723998822054 

Date
2011-01-03    1.000000
2011-01-04    1.005219
2011-01-05    1.013442
2011-01-06    1.012622
2011-01-07    1.019874
2011-01-10    1.039081
2011-01-11    1.036623
2011-01-12    1.045059
2011-01-13    1.048882
2011-01-14    1.057378
2011-01-18    1.033620
2011-01-19    1.028128
2011-01-20    1.009437
2011-01-21    0.991352
2011-01-24    1.023910
...
2015-11-30    2.698560
2015-12-01    2.676661
2015-12-02    2.652481
2015-12-03    2.627845
2015-12-04    2.715212
2015-12-07    2.698103
2015-12-08    2.696963
2015-12-09    2.637426
2015-12-10    2.649972
2015-12-11    2.581767
2015-12-14    2.565799
2015-12-15    2.520404
2015-12-16    2.539794
2015-12-17    2.485960
2015-12-18    2.418667
Length: 1250 

Date
2012-01-31    0.127111
2012-02-29    0.188311
2012-03-30    0.105283
2012-04-30   -0.025970
2012-05-31   -0.010702
2012-06-29    0.010853
2012-07-31    0.045822
2012-08-31    0.093877
2012-09-28    0.002796
2012-10-31   -0.107600
2012-11-30   -0.012375
2012-12-31   -0.090743
Freq: BM
Date
2012-01    0.127111
2012-02    0.188311
2012-03    0.105283
2012-04   -0.025970
2012-05   -0.010702
2012-06    0.010853
2012-07    0.045822
2012-08    0.093877
2012-09    0.002796
2012-10   -0.107600
2012-11   -0.012375
2012-12   -0.090743
Freq: M
[Finished in 3.0s]

2、分组变换和分析

在第九章中，已经学习了分组统计的基础，还学习了如何对数据集的分组应用自定义的变换函数。

#-*- coding:utf-8 -*-
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import datetime as dt
from pandas import Series,DataFrame
from datetime import datetime
from dateutil.parser import parse
import time
from pandas.tseries.offsets import Hour,Minute,Day,MonthEnd
import pytz
import random;random.seed(0)
import string

#首先生成1000个股票代码
N = 1000
def rands(n):
    choices = string.ascii_uppercase  #choices为ABCD……XYZ
    return ''.join([random.choice(choices) for _ in xrange(n)])
tickers = np.array([rands(5) for _ in xrange(N)])
print tickers,'\n'
#然后创建一个含有3列的DataFrame来承载这些假想数据，不过只选择部分股票组成该投资组合
M = 500
df = DataFrame({'Momentum':np.random.randn(M) / 200 + 0.03,
    'Value':np.random.randn(M) / 200 + 0.08,
    'ShortInterest':np.random.randn(M) / 200 - 0.02},
    index = tickers[:M])
print df,'\n'
#接下来创建一个行业分类
ind_names = np.array(['FINANCIAL','TECH'])
sampler = np.random.randint(0,len(ind_names),N)
industries = Series(ind_names[sampler],index = tickers,name = 'industry')
print industries,'\n'
#现在就可以进行分组并执行分组聚合和变换了
by_industry = df.groupby(industries)
print by_industry.mean(),'\n'
print by_industry.describe(),'\n'
#需要对这些行业分组的投资组合进行各种变换，可以编写自定义的变换函数，例如行业内标准化处理，它广泛应用于股票资产投资组合的构建过程
#行业内标准化处理
def zscore(group):
    return (group - group.mean()) / group.std()
df_stand = by_industry.apply(zscore)
#标准化以后，各行业的均值为0，标准差为1
print df_stand.groupby(industries).agg(['mean','std']),'\n'
#内置变换函数（比如rank）的用法会更简洁一些
ind_rank = by_industry.rank(ascending = False)
print ind_rank.groupby(industries).agg(['min','max']),'\n'
#在股票投资组合的定量分析中，排名和标准化是一种常见的变换运算组合。通过rank和zscore链接在一起即可完成整个过程
#行业内排名和标准化,这是把排名进行了标准化
print by_industry.apply(lambda x : zscore(x.rank())).head()

>>>
['VTKGN' 'KUHMP' 'XNHTQ' 'GXZVX' 'ISXRM' 'CLPXZ' 'MWGUO' 'ASKVR' 'AMWGI'
 'WEOGZ' 'ULCIN' 'YCOSO' 'VOZPP' 'LPKOH' 'EEPRM' 'CTWYV' 'XYOKS' 'HVWXP'
 'YPLRZ' 'XUCPM' 'QVGTD' 'FUIVC' 'DSBOX' 'NRAQP' 'OKJZA' 'AYEDF' 'UYALC'
 'GFQJE' 'NBCZF' 'JTVXE' 'RZBRV' 'IGPLE' 'MKONI' 'JVGOA' 'TIBHG' 'YJHJY'
 'QQSKK' 'QAFIG' 'QJWOK' 'KSKRB' 'LGENM' 'OTWMI' 'MVWVE' 'ZQCSZ' 'KRIFS'
 'AVNCD' 'QWHZC' 'WKCHL' 'UWDNQ' 'JWHAB' 'ROYYX' 'BTSRS' 'XQJNF' 'PADIU'
 'SIQBE' 'ZHKOH' 'MGBEN' 'BKIKC' 'XMVZI' 'MSLHT' 'XXQJZ' 'QBCTB' 'AKNLM'
 'PRKJZ' 'GULJB' 'WSXLR' 'DKFBY' 'FDFJO' 'DZZDK' 'RWMXI' 'MMRFP' 'FIZXV'
 'ADGUV' 'PSUBC' 'WBFBA' 'VIEDR' 'ZNXNO' 'RUTZT' 'XFNPV' 'MUKPW' 'URAEN'
 'GBWYH' 'KVBQD' 'HVBAK' 'MWSRD' 'ZKPKB' 'MDAQQ' 'COJJU' 'MWPMQ' 'IDRQU'
 'DXUXW' 'RVNUE' 'ULTLU' 'BBYMX' 'YROFC' 'VXUSK' 'HCLOX' 'YKCUT' 'ALRAX'
 'ZSCBJ' 'AJAZV' 'BXFFR' 'YDAJA' 'PWECI' 'YDZJM' 'HYYQE' 'ZCPEX' 'YUIGT'
 'HKBDA' 'CBKOT' 'DKQCL' 'JYBKK' 'SIFHM' 'YUHOR' 'ULKTL' 'GLYDM' 'QMFAS'
 'QAHTQ' 'OESMR' 'TGTHZ' 'DWBGN' 'PKCGH' 'TXPAU' 'HINGX' 'EKHNO' 'QNKQK'
 'UUHJQ' 'ESJPD' 'RJMKM' 'SIQBH' 'TBQAM' 'XANBW' 'RTRAB' 'QZWSS' 'FTHCL'
 'IEKXL' 'LSNDX' 'LUKUK' 'FFYPB' 'KGCEB' 'QEPPS' 'NHWJL' 'QNYYY' 'YPMSF'
 'GBEAR' 'DURZK' 'XLICW' 'UILIA' 'BJFNE' 'FRTIW' 'GISBY' 'BLSBV' 'ZLDCC'
 'TKXLC' 'LTVBE' 'MDWYI' 'LOHOF' 'HLPNG' 'GDUCT' 'GHTRT' 'NWDQD' 'TJRSR'
 'FVGNR' 'GQHEV' 'OIPAD' 'KZNBT' 'UUOSF' 'TVTJP' 'QXCVN' 'JLAFQ' 'RMYMI'
 'WGPSV' 'UJBAS' 'ZILSR' 'GRHJO' 'TDAQA' 'BFRBB' 'ZKXFL' 'JEIZT' 'JKGNT'
 'RMBXK' 'KADWN' 'TDIVV' 'GAUEU' 'RECYP' 'QLDPG' 'UTAYA' 'CHDGJ' 'TKHMK'
 'IXOZU' 'OGRLS' 'KMATA' 'RPUHR' 'FNIZZ' 'FOIZY' 'PSRJX' 'XITAV' 'OYJQI'
 'UPZAD' 'BDYYM' 'YVUTE' 'OLYEE' 'RECNU' 'PTGHL' 'ZSYNO' 'ZEUUV' 'TERYO'
 'JYOKP' 'UFANY' 'RQQMT' 'GXHYY' 'CLTLN' 'USYEY' 'YQYGW' 'UPCAA' 'GTKUQ'
 'KWAMV' 'DSIAM' 'NBOJA' 'ECOBY' 'VYIXZ' 'THRPK' 'HBDDM' 'QTBVB' 'OTQYI'
 'PCOVF' 'GSGGY' 'ZEXOB' 'PQATV' 'BQLGL' 'EIRMO' 'OVIVC' 'LJLVN' 'ZWDIA'
 'TAXFK' 'BIKBT' 'SJVCB' 'JXTRO' 'UKAUE' 'KJDJE' 'QQALO' 'WMCBW' 'UWGQC'
 'VIYMA' 'XQHAJ' 'EODEX' 'QGWQY' 'MXRBG' 'HEGFW' 'MWDOA' 'YAKUZ' 'AVNAU'
 'CPURJ' 'ALXIG' 'DNNBK' 'RZLLM' 'FKQKP' 'VZXJA' 'PMGBI' 'UZCWB' 'SAKWK'
 'YSPEI' 'KPZHN' 'YIQTQ' 'TFYEP' 'HQHLR' 'GSJDP' 'ELKBS' 'RUOOE' 'FFNVJ'
 'WTSID' 'ZWKWX' 'INISX' 'ZTHWZ' 'JYNZZ' 'VREAP' 'SYNSQ' 'FQZCR' 'PJUAX'
 'VMCLP' 'GMUXO' 'VCWXE' 'VWWNP' 'FSKAD' 'KXOXY' 'CPINL' 'MCVMQ' 'MEOEW'
 'VDBBK' 'YOGFC' 'DVDWV' 'DOAWO' 'TMRYO' 'WICAF' 'VIFMY' 'NICOF' 'JJTGY'
 'TMWJJ' 'DUKNM' 'RJXLJ' 'KTZWM' 'HLIGE' 'YMCJK' 'NZZOQ' 'RNMIR' 'CIXFZ'
 'ZOBCF' 'ICUJG' 'BJADP' 'YFTFA' 'XVBEG' 'YJULJ' 'TQHPS' 'VRQPC' 'YSHSQ'
 'RJORF' 'NDCXD' 'XMLIK' 'JOIVG' 'GMYAS' 'AKTLL' 'GMFHQ' 'PYZNC' 'HNRYE'
 'AWUTM' 'RKEKU' 'UYXRN' 'SEYSP' 'LQQXO' 'FLGXV' 'OFBDL' 'RFRWT' 'LQZXI'
 'REOJL' 'LRVMD' 'TTYKM' 'OXSAF' 'WPWKF' 'AZDQM' 'JNCZM' 'AKTIT' 'TGZAW'
 'NDGPH' 'VFJNI' 'VGCEQ' 'OBZMI' 'SALRZ' 'TXDLA' 'HJIJU' 'EVOIO' 'EMAWI'
 'IZPKU' 'BONWP' 'MNUJO' 'SZSZK' 'PTJGZ' 'JZWFV' 'ZHRUC' 'VISYA' 'PHCSZ'
 'NJLKN' 'KCZZE' 'GLSAV' 'QHWRI' 'OZBSW' 'SDPUK' 'PGIVM' 'LDJNG' 'VJGIV'
 'XYATN' 'DGHKM' 'YBSWJ' 'GFHDO' 'GAGVK' 'WYGOW' 'PEGZH' 'WUTSU' 'WBENF'
 'NMDCA' 'VCZZT' 'LHKIK' 'SXEGF' 'BWNBL' 'LUTDQ' 'NADRJ' 'ZNRDM' 'TVFKM'
 'LMHVX' 'JQJPS' 'NRTVE' 'FNNVN' 'XUNVM' 'ILLQB' 'SZLBF' 'CGUAW' 'YEEZJ'
 'VAZAP' 'YVIVK' 'MJJPU' 'STANJ' 'FXFEE' 'RPNPY' 'WXBXA' 'QYNKI' 'XYQSI'
 'DZRHZ' 'PIXCU' 'ECGSP' 'KEYTR' 'VUCUV' 'TMRCT' 'GUQNN' 'BBAUD' 'DKZXI'
 'VCKPZ' 'BKXAP' 'KOSKX' 'YZBVW' 'DYDFY' 'VOHGK' 'AQBUB' 'AHUVN' 'YCITI'
 'DPBJG' 'IMNCI' 'JKMLB' 'FQVND' 'BEJOR' 'NOJRS' 'KVTXM' 'IUAJZ' 'INGCC'
 'LQONC' 'BJYEH' 'MXYAQ' 'GRTXR' 'WUEBT' 'NZEKH' 'WMXSZ' 'PZELP' 'ZOWQN'
 'KJHFZ' 'NWXYG' 'IQIDT' 'ONSCX' 'MRPPS' 'CMFKN' 'JKTBY' 'PEOCN' 'RKIRY'
 'WKWCB' 'ZTPOI' 'XWMFR' 'SZUCZ' 'WPITP' 'COAUV' 'SCPKD' 'XYXNW' 'FHXPF'
 'DFMHT' 'HCXRZ' 'EWANM' 'DVHXS' 'WWUTA' 'DFPAD' 'MBIFE' 'IWGQT' 'REJHO'
 'ZFOBJ' 'YXCWS' 'XLKXN' 'TEBLI' 'NIWTJ' 'DSODA' 'QNOKM' 'KCNDR' 'TEFGP'
 'KXONF' 'CYCDF' 'OQLKQ' 'GUQPA' 'ITFQZ' 'LNFAG' 'MPVHI' 'SRSWC' 'DMPRF'
 'DXGAH' 'NQTDN' 'ISJVE' 'ZNLSJ' 'ALHRN' 'VMEDO' 'GFYDX' 'NYVHM' 'CJYCG'
 'BWRPM' 'GPSUE' 'QRPSN' 'YQQAD' 'PTDQE' 'TVQBH' 'HMUPZ' 'SDZBI' 'QKAHG'
 'UPDWF' 'IWTKN' 'ZSSRZ' 'YHLQG' 'QXHJL' 'KQBUH' 'QLPON' 'EACKG' 'MMNDM'
 'YEAIS' 'WCAIQ' 'XIUDQ' 'GTXLR' 'JWKPZ' 'OLCYN' 'SRGQC' 'BVPHN' 'ORADC'
 'TLFJR' 'LOYKC' 'CSICU' 'XCQTG' 'VRLEG' 'VESOO' 'ADIQJ' 'GJMPO' 'JLUPZ'
 'PHNMW' 'TWSGH' 'EWXIA' 'MUSRA' 'CSVEV' 'YPOAK' 'MYLAO' 'BZRSS' 'YKHCA'
 'MTTAQ' 'VWUKS' 'SBBIQ' 'JQTUH' 'ZOQQR' 'ERLZS' 'ZZVPP' 'MJKXQ' 'EALLB'
 'FIJQE' 'VMBCY' 'AQERZ' 'XLLHL' 'YAMXC' 'DVHUH' 'AVILB' 'QVFYQ' 'OFWLB'
 'YJHBA' 'BWWMC' 'DYOUB' 'BUDVY' 'LCSLN' 'XODJW' 'NCNAW' 'GSZXN' 'ISOXG'
 'SDKUJ' 'HJJAD' 'TSQDD' 'MMDZV' 'WERVI' 'ZCUDG' 'EDRGU' 'UYUZO' 'AIKZK'
 'HUXBZ' 'SZQAR' 'FZYWS' 'GYVQE' 'FOPKV' 'RGAPI' 'XGOFZ' 'QTXLO' 'LQIVJ'
 'UAJMX' 'STQXS' 'QXTAW' 'ETKKE' 'LZVTQ' 'FBYXA' 'XTCEE' 'GXKOL' 'MGIGH'
 'PAYNN' 'KTTSZ' 'KCUSA' 'MVYJM' 'LTSME' 'PAJIB' 'CULDY' 'ILSEU' 'VMSSZ'
 'UJNKN' 'XCXND' 'YFAMO' 'BQOOC' 'JDMJI' 'WQCRZ' 'JURMK' 'FKGMR' 'XDVTQ'
 'EBDIH' 'VIEZS' 'UMCPL' 'ICIHJ' 'SDJTI' 'WWEQQ' 'EOMGS' 'XXCJC' 'MRSBC'
 'QVPCC' 'PFTHV' 'XNSTQ' 'QKXEE' 'SFNXJ' 'TWRCN' 'UZLBJ' 'MYBXL' 'CTDDG'
 'ORWPQ' 'MNRHH' 'QQEFO' 'VIEBN' 'NPORW' 'IUFIM' 'NTATU' 'AOADW' 'BXRTR'
 'TTXJJ' 'QNRJK' 'KBTOX' 'TKUBQ' 'YXIHH' 'XIKIG' 'WLNKI' 'KXHSF' 'XMHLT'
 'WVDZM' 'YEYFW' 'HVEWR' 'DYLEV' 'BATCT' 'CYDOQ' 'JCMIX' 'FFPLH' 'DVCXY'
 'DYGUI' 'LSOTK' 'BIXUY' 'PIMMG' 'WBIZO' 'YAVQW' 'TZITV' 'SUVHH' 'KAXVD'
 'VIPML' 'PXKAW' 'YUEKT' 'WWYQD' 'KYDYJ' 'PVCCM' 'XZREU' 'JGPLN' 'ZAWLV'
 'WTMNP' 'KSWIY' 'OHESH' 'VYJJH' 'GZVWA' 'YVVYK' 'BONFT' 'ZSUUV' 'EPPWL'
 'GNMAB' 'EMRNO' 'ZCJOU' 'WQRXU' 'PAKBZ' 'VICOJ' 'SVPVA' 'GLMVE' 'ONQAB'
 'CKPTQ' 'CWKVE' 'JRQNY' 'VPRKN' 'QVFLE' 'FADTI' 'HDOKB' 'JUTZW' 'MUUKK'
 'OLQVX' 'QNFKF' 'SODEA' 'CQQNU' 'OGTJB' 'FLPUW' 'UTPFR' 'SGJHZ' 'SJFIG'
 'VEJNG' 'EYXAN' 'BLCUF' 'HCZNK' 'OEUHW' 'THMHY' 'WORCU' 'JGIXC' 'ZMQNB'
 'TKMVI' 'DBRBP' 'BCKHC' 'YYZZX' 'OKTNF' 'UEQYN' 'DJNLD' 'PWZER' 'ADNPG'
 'TXZCR' 'NSYHW' 'CBYGS' 'FPIST' 'XULDR' 'LSZIL' 'IIGJJ' 'JYJAZ' 'PIUAW'
 'DADVB' 'XHFRG' 'OTRIQ' 'QALQJ' 'EXAWE' 'ZXCTR' 'WMIUT' 'NZUMY' 'NVBDF'
 'GDBOP' 'SPLLA' 'QQQZS' 'FPORP' 'TLOYG' 'RTVOZ' 'ZNLCP' 'IRSWT' 'VVZIP'
 'OORYA' 'IMNXM' 'GWNUG' 'YKLMI' 'TOPPH' 'ICKGJ' 'QRTFE' 'ZMMCR' 'EBGZI'
 'BREHM' 'OHYTQ' 'BVVVV' 'EXHGA' 'EJGWB' 'LJWVI' 'RLGSM' 'STOGD' 'ALRVH'
 'BMIIB' 'NLSRJ' 'BZFTO' 'ATZDS' 'OOLLE' 'JRWTQ' 'FAWTY' 'DZIOA' 'UYYED'
 'OKAHU' 'TGXJU' 'IZRJB' 'EYOUF' 'NPYNY' 'IPQCE' 'GGEKC' 'DWELC' 'UGRVK'
 'FELPR' 'PGADL' 'ZOZVZ' 'HRLWP' 'KYVML' 'KKIEV' 'DQEWF' 'DAXUI' 'WNFOA'
 'SHJWQ' 'YFAWP' 'DGYPO' 'UXKVW' 'YMXVM' 'SDTKV' 'IUHMK' 'ZGVVY' 'SMYAX'
 'TFHWC' 'HDFDJ' 'WPECZ' 'GHEHY' 'JKIPN' 'GCOOB' 'ILMIR' 'UDKRP' 'WWOXU'
 'DAKJA' 'VNZVV' 'KYSCO' 'FQKBX' 'XQFKS' 'DFCYT' 'DGRZF' 'WLWAN' 'KUYCT'
 'JWWZN' 'MFBXC' 'LCAIC' 'HZGUU' 'BKDID' 'DSBMO' 'LGQCE' 'HLFQG' 'MURPV'
 'KLKDP' 'MUPIW' 'HHWZF' 'FPAVL' 'TAUOA' 'BKQLQ' 'XJKUB' 'IBQRR' 'QTAQQ'
 'VTAPK' 'HCDEG' 'MPGFN' 'MBFKY' 'LGWZE' 'WMGVO' 'OSKST' 'VBHPR' 'PUIQN'
 'VHNGY' 'ZHWLH' 'JTZVV' 'HFGYE' 'FUWGN' 'JWPMR' 'ZQVVG' 'KFPUK' 'ILSBY'
 'ROACD' 'QOEWI' 'DHTMQ' 'HQGAS' 'LHNJU' 'ZQBRA' 'KCWAR' 'MNGJL' 'LMVQW'
 'NNQST' 'OKHTB' 'YZXXY' 'PVELA' 'JLESE' 'ETXYW' 'FPNBF' 'OWTVL' 'YPHIJ'
 'DQNVC' 'DIFGJ' 'JNTNX' 'BRRYO' 'SLBCL' 'QJEWY' 'IHDZO' 'OIUER' 'RYVLS'
 'NDOSY' 'OGNSH' 'DFHFH' 'BLRAE' 'CKWGK' 'JECFB' 'KTHZN' 'TOOUU' 'FEEGC'
 'GKQAP' 'SXROH' 'JPUJR' 'JQBCR' 'WITUB' 'RLFFV' 'RKMEZ' 'NBKWI' 'TCTPL'
 'FMUBG' 'HHRYP' 'RMMSR' 'JMBIT' 'ZMLDR' 'XBQFD' 'RHCSW' 'PTRNL' 'OHAQX'
 'JLSAG' 'UQBJP' 'DYEPB' 'GDTZX' 'FQXRB' 'LIQBR' 'BBFWT' 'GAGYO' 'CSQWZ'
 'WRWQF' 'NHGEB' 'HWNNC' 'YDZEB' 'YAHRO' 'TITBA' 'GVCTY' 'ZCGBT' 'LGXPZ'
 'RCDDJ' 'UXBKY' 'UHXDI' 'FLNBE' 'QVCYN' 'UBJMO' 'ZNXZX' 'JWISS' 'PXUVL'
 'XSIKG' 'WJJKO' 'HVRUB' 'JFFIW' 'JBWUO' 'BDJKH' 'TZLEL' 'DMKZJ' 'DYSSI'
 'FSHPC' 'LQOQF' 'LBBFQ' 'UPJAS' 'WAQIK' 'TLOSR' 'MNQAA' 'MSYNR' 'XCDMO'
 'HKWNO' 'YPMEE' 'NBNWK' 'VTVIP' 'QCERS' 'BMMLT' 'ZAYTJ' 'GPNYZ' 'UWRUN'
 'SLXXZ' 'GFQJK' 'URWVM' 'CKUJV' 'KVTRA' 'YJCAW' 'KPZYQ' 'TQKDF' 'HFYFG'
 'SZQHV' 'EQMTM' 'QAVSF' 'YZQVZ' 'HEIZH' 'LWELG' 'KYLBX' 'WIBMQ' 'LBCTN'
 'QHLIR' 'LCRZK' 'AOQJX' 'YMNLR' 'BHUFN' 'FCKOG' 'ILSDP' 'PZPKM' 'PNRHG'
 'ZYTZZ'] 

<class 'pandas.core.frame.DataFrame'>
Index: 500 entries, VTKGN to PTDQE
Data columns:
Momentum         500  non-null values
ShortInterest    500  non-null values
Value            500  non-null values
dtypes: float64(3) 

VTKGN    FINANCIAL
KUHMP         TECH
XNHTQ         TECH
GXZVX    FINANCIAL
ISXRM         TECH
CLPXZ    FINANCIAL
MWGUO    FINANCIAL
ASKVR         TECH
AMWGI         TECH
WEOGZ         TECH
ULCIN    FINANCIAL
YCOSO    FINANCIAL
VOZPP         TECH
LPKOH         TECH
EEPRM    FINANCIAL
...
HEIZH    FINANCIAL
LWELG    FINANCIAL
KYLBX         TECH
WIBMQ         TECH
LBCTN         TECH
QHLIR         TECH
LCRZK         TECH
AOQJX         TECH
YMNLR         TECH
BHUFN         TECH
FCKOG    FINANCIAL
ILSDP    FINANCIAL
PZPKM         TECH
PNRHG         TECH
ZYTZZ    FINANCIAL
Name: industry, Length: 1000 

           Momentum  ShortInterest     Value
industry                                    
FINANCIAL  0.030406      -0.019782  0.079936
TECH       0.029859      -0.019990  0.079252 

                   Momentum  ShortInterest       Value
industry                                              
FINANCIAL count  249.000000     249.000000  249.000000
          mean     0.030406      -0.019782    0.079936
          std      0.005043       0.004875    0.004700
          min      0.018415      -0.032969    0.068910
          25%      0.026759      -0.023331    0.076816
          50%      0.029893      -0.019888    0.079846
          75%      0.033647      -0.016402    0.082657
          max      0.043659      -0.005031    0.093285
TECH      count  251.000000     251.000000  251.000000
          mean     0.029859      -0.019990    0.079252
          std      0.005144       0.004759    0.005039
          min      0.016133      -0.034532    0.063635
          25%      0.026706      -0.023397    0.076275
          50%      0.029469      -0.020236    0.079372
          75%      0.033749      -0.016660    0.083053
          max      0.042830      -0.006840    0.092007 

               Momentum       ShortInterest              Value     
                   mean  std           mean  std          mean  std
industry                                                           
FINANCIAL -1.110223e-15    1   1.213665e-15    1 -2.380960e-16    1
TECH      -3.696246e-15    1   1.084568e-15    1  1.438977e-14    1 

           Momentum       ShortInterest       Value     
                min  max            min  max    min  max
industry                                                
FINANCIAL         1  249              1  249      1  249
TECH              1  251              1  251      1  251 

       Momentum  ShortInterest     Value
VTKGN -1.332883       1.180157 -1.263462
KUHMP -0.964165      -0.096417 -0.771332
XNHTQ  1.349832      -0.909070 -0.165285
GXZVX -1.249578      -1.110736  1.055199
ISXRM  0.922844      -1.005487  1.101903
[Finished in 0.8s]

• 分组因子暴露

因子分析（factor analysis）是投资组合定量管理中的一种技术。投资组合的持有量和性能（收益与损失）可以被分解为一个或多个表示投资组合权重的因子（风险因子就是其中之一）。例如，某只股票与某个基准（比如标普500指数）的协动性被称为其beta风险系数。下面以一个人为构成的投资的投资组合为例进行讲解，它由三个随机生成的因子（通常称为因子载荷）和一些权重构成。

#-*- coding:utf-8 -*-
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import datetime as dt
from pandas import Series,DataFrame
from datetime import datetime
from dateutil.parser import parse
import time
from pandas.tseries.offsets import Hour,Minute,Day,MonthEnd
import pytz
import random;random.seed(0)
import string
from numpy.random import rand
import pandas.io.data as web

#首先生成1000个股票代码
N = 1000
def rands(n):
    choices = string.ascii_uppercase  #choices为ABCD……XYZ
    return ''.join([random.choice(choices) for _ in xrange(n)])
tickers = np.array([rands(5) for _ in xrange(N)])


#然后创建一个含有3列的DataFrame来承载这些假想数据，不过只选择部分股票组成该投资组合
M = 500
df = DataFrame({'Momentum':np.random.randn(M) / 200 + 0.03,
    'Value':np.random.randn(M) / 200 + 0.08,
    'ShortInterest':np.random.randn(M) / 200 - 0.02},
    index = tickers[:M])

#接下来创建一个行业分类
ind_names = np.array(['FINANCIAL','TECH'])
sampler = np.random.randint(0,len(ind_names),N)
industries = Series(ind_names[sampler],index = tickers,name = 'industry')

fac1,fac2,fac3 = np.random.rand(3,1000)
ticker_subset = tickers.take(np.random.permutation(N)[:1000])
print ticker_subset[:10],'\n'

#因子加权和以及噪声
port = Series(0.7 * fac1 - 1.2 * fac2 + 0.3 * fac3 + rand(1000),
    index = ticker_subset)
factors = DataFrame({'f1':fac1,'f2':fac2,'f3':fac3},index = ticker_subset)
print factors.head(),'\n'
#各因子与投资组合之间的矢量相关性可能说明不了什么问题
print factors.corrwith(port),'\n'
#计算因子暴露的标准方式是最小二乘回归。
print pd.ols(y = port,x = factors).beta
#可以看出，由于没有给投资组合添加过多的随机噪声，所以原始因子基本恢复了。还可以通过groupby计算各行业的暴露量
def beta_exposure(chunk,factors = None):
    return pd.ols(y = chunk,x = factors).beta
#根据行业进行分组，并应用该函数
by_ind = port.groupby(industries)
exposures = by_ind.apply(beta_exposure,factors = factors)
print exposures.unstack()
>>>
['ECOBY' 'BIXUY' 'WICAF' 'UAJMX' 'VGCEQ' 'ECGSP' 'REJHO' 'KEYTR' 'LWELG'
 'UZLBJ'] 

             f1        f2        f3
ECOBY  0.851706  0.259984  0.097494
BIXUY  0.937227  0.743504  0.883864
WICAF  0.833994  0.429274  0.871291
UAJMX  0.598321  0.697040  0.631816
VGCEQ  0.157317  0.438006  0.410215 

f1    0.426756
f2   -0.708818
f3    0.153762 

f1           0.717723
f2          -1.261801
f3           0.307803
intercept    0.507541
                 f1        f2        f3  intercept
industry                                          
FINANCIAL  0.702203 -1.264149  0.275483   0.538837
TECH       0.732947 -1.260257  0.342993   0.474543
[Finished in 0.9s]

• 十分位和四分位分析

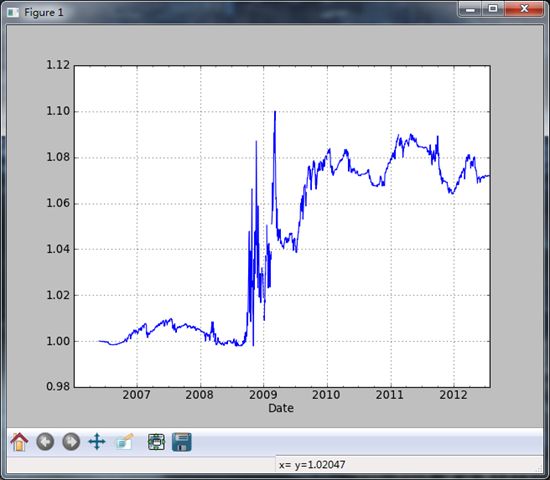
基于样本分位数的分析是金融分析师们的另一个重要工具，例如，股票投资组合的性能可以根据各股的市盈率被划分入四分位。

#-*- coding:utf-8 -*-
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import datetime as dt
from pandas import Series,DataFrame
from datetime import datetime
from dateutil.parser import parse
import time
from pandas.tseries.offsets import Hour,Minute,Day,MonthEnd
import pytz
import random;random.seed(0)
import string
from numpy.random import rand
import pandas.io.data as web

#通过pandas.qcut和groupby可以轻松实现分位数分析
data = web.get_data_yahoo('SPY','2006-01-01','2012-07-27')  #设置一个尾巴值
print data
#接下来计算日收益率，并编写一个用于将收益率转换为趋势信号的函数
px = data['Adj Close']
returns = px.pct_change()

def to_index(rets):
    index = (1 + rets).cumprod()
    #下面是将第一个有效值的位置拿出来
    first_loc = max(index.notnull().argmax() - 1,0)
    index.values[first_loc] = 1
    return index

def trend_signal(rets,lookback,lag):
    signal = pd.rolling_sum(rets,lookback,min_periods = lookback - 5)
    return signal.shift(lag)
#通过该函数，我们可以单纯地创建和测试一种根据每周五动量信号进行交易的交易策略
signal = trend_signal(returns,100,3)
print signal
trade_friday = signal.resample('W-FRI').resample('B',fill_method = 'ffill')
trade_rets = trade_friday.shift(1) * returns
#然后将该策略的收益率转换为一个收益指数，并绘制一张图表
to_index(trade_rets).plot()
plt.show()
#假如希望将该策略的性能按不同大小的交易期波幅进行划分。年度标准差是计算波幅的一种简单办法，可以通过计算夏普比率来观察不同波动机制下的风险收益率：
vol = pd.rolling_std(returns,250,min_periods = 200) * np.sqrt(250)
def sharpe(rets,ann = 250):
    return rets.mean() / rets.std() * np.sqrt(ann)
#现在利用qcut将vol划分为4等份，并用sharpe进行聚合:
print trade_rets.groupby(pd.qcut(vol,4)).agg(sharpe)
#上面的结果说明，该策略在波幅最高时性能最好
>>>
<class 'pandas.core.frame.DataFrame'>
DatetimeIndex: 1655 entries, 2006-01-03 00:00:00 to 2012-07-27 00:00:00
Data columns:
Open         1655  non-null values
High         1655  non-null values
Low          1655  non-null values
Close        1655  non-null values
Volume       1655  non-null values
Adj Close    1655  non-null values
dtypes: float64(5), int64(1)
Date
2006-01-03   NaN
2006-01-04   NaN
2006-01-05   NaN
2006-01-06   NaN
2006-01-09   NaN
2006-01-10   NaN
2006-01-11   NaN
2006-01-12   NaN
2006-01-13   NaN
2006-01-17   NaN
2006-01-18   NaN
2006-01-19   NaN
2006-01-20   NaN
2006-01-23   NaN
2006-01-24   NaN
...
2012-07-09    0.028628
2012-07-10    0.031504
2012-07-11    0.014558
2012-07-12    0.014559
2012-07-13    0.010499
2012-07-16   -0.000425
2012-07-17   -0.007916
2012-07-18    0.008422
2012-07-19    0.009289
2012-07-20    0.011745
2012-07-23    0.016956
2012-07-24    0.017897
2012-07-25    0.005832
2012-07-26   -0.000354
2012-07-27   -0.014123
Length: 1655
[0.0954, 0.16]    0.491098
(0.16, 0.188]     0.425300
(0.188, 0.231]   -0.687110
(0.231, 0.457]    0.570821
[Finished in 6.1s]