ACM/ICPC 之 一道不太简单的DP面试题(Geeksforgeeks)

题面来源：geeksforgeeks/1993

题解：geeksforgeeks

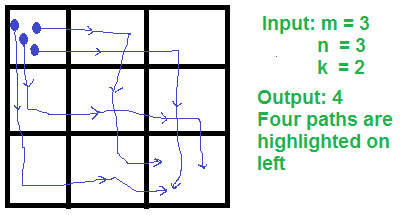
题目简述：给一个m*n的矩阵，计算从(1,1)到(m,n)的所有不回退路径中，经过k次转向后的路径有多少条

　　　　　输入T个样例，每个样例三个数据，依次是m，n，k。

　　　　　输出路径条数。

给个题解中的图解：

　　

 

测试数据:

Sample Input

3
2 2 3
2 3 1
4 4 4

Sample Output

2
2
18

 

已经贴了题面来源就暂时不贴全部的题目了，偶然发现了这道DP，貌似是FB的面试题，是道非常好的题目。

测试代码如下(建议尝试一次)：

 

 1 #include<iostream>
 2 using namespace std;
 3 
 4 #define MAX 100
 5 
 6 //dp[i][j][k][d]
 7 //从(0,0)->(i,j)经过k次转向，且上一次经过d的总路径
 8 //d = 0: 横; d=1: 竖
 9 int dp[MAX][MAX][MAX][2];
10 
11 int countPathsUtil(int i, int j, int k, int d)
12 {
13     if (i < 0 || j < 0)
14         return 0;
15 
16     if (i == 0 && j == 0)    //到达原点
17         return 1;
18 
19     if (k == 0)
20     {
21         if (d == 0 && i == 0) return 1;    //到左侧边，且为竖向
22         if (d == 1 && j == 0) return 1; //到顶侧边，且为横向
23         return 0;
24     }
25 
26     //记忆化
27     if (dp[i][j][k][d] != -1)
28         return dp[i][j][k][d];
29 
30     if (d == 0)    //若横向走
31         return dp[i][j][k][d] = countPathsUtil(i, j - 1, k, d) +    //继续横向
32         countPathsUtil(i - 1, j, k - 1, !d);    //转向
33     //竖向同理
34     return dp[i][j][k][d] = countPathsUtil(i - 1, j, k, d) +    //继续竖向
35         countPathsUtil(i, j - 1, k - 1, !d);    //转向
36 }
37 
38 int countPaths(int i, int j, int k)
39 {
40     if (i == 0 && j == 0)
41         return 1;
42     memset(dp, -1, sizeof dp);
43 
44     return countPathsUtil(i - 1, j, k, 1) +  // 减治到上格
45         countPathsUtil(i, j - 1, k, 0); // 减治到左格
46 }
47 
48 int main()
49 {
50     int m = 3, n = 3, k = 2;
51     cout << countPaths(m - 1, n - 1, k) << endl;
52     return 0;
53 }

= 。=