基于二叉树和数组实现限制长度的最优Huffman编码

具体介绍详见上篇博客：基于二叉树和双向链表实现限制长度的最优Huffman编码
基于数组和基于链表的实现方式在效率上有明显区别：
编码256个符号，符号权重为1...256，限制长度为16，循环编码1w次，Release模式下。基于链表的耗时为8972ms，基于数组的耗时为1793ms，速度是链表实现方式的5倍.
详细代码例如以下：

//Reference:A fast algorithm for optimal length-limited Huffman codes.pdf,http://pan.baidu.com/s/1o6E19Bs
//author:by Pan Yumin.2014-06-18
//with the method of BinaryTree and linked-list
#include <stdio.h>
#include <memory.h>
#include <malloc.h>

#define  MaxSymbols 256	//the Maximum Number of Symbols
#define  MaxHuffLen	16	//the Limited Length

typedef unsigned char boolean;
#ifndef FALSE			//in case these macros already exist
#define FALSE	0		//values of boolean
#endif

#ifndef TRUE
#define TRUE	1
#endif

typedef struct __Node{
	int width;
	int weight;
	int index;
	int depth;

	struct __Node *left;	//left child
	struct __Node *right;	//right child
}Node;

typedef struct __HuffTable{
	unsigned int index;
	unsigned int len;
	unsigned int code;
}HuffTable;

//Test memory leak
/*int g_malloc = 0,g_free = 0;

void* my_malloc(int size){
	g_malloc++;
	return malloc(size);
}
void my_free(void *ptr){
	if(ptr){
		g_free++;
		free(ptr);
		ptr = NULL;
	}
}
#define malloc my_malloc
#define free my_free*/

//Get the smallest term in the diadic expansion of X
int GetSmallestTerm(int X)
{
	int N=0;
	while((X & 0x01) == 0){
		X >>= 1;
		N++;
	}
	return 1<<N;
}
void RemoveNodeMark(Node *tree,unsigned char *Flag,int Symbols)
{
	if(tree->left == NULL && tree->right == NULL){
		Flag[tree->depth*Symbols+tree->index] = 0;	//set the nodemark zero
	}
	if(tree->left){
		RemoveNodeMark(tree->left,Flag,Symbols);
	}
	if(tree->right){
		RemoveNodeMark(tree->right,Flag,Symbols);
	}
}

void PrintHuffCode(HuffTable Huffcode)
{
	int i;
	for(i=Huffcode.len-1;i>=0;i--){
		printf("%d",(Huffcode.code>>i) & 0x01);
	}
}
void GenerateHuffmanCode(HuffTable *HuffCode,unsigned char *Flag,int L,int Symbols,int *SortIndex)
{
	char Code[17];
	int Pre_L = 0;
	int i=0,j=0;
	unsigned int codes[MaxHuffLen+2]={0},rank[MaxHuffLen+1] = {0};	//rank: the number of symbols in every length
	//find the first code
	for(i=0;i<Symbols;i++){
		for(j=0;j<L;j++){
			HuffCode[i].len += Flag[j*Symbols+i];
		}
		if(HuffCode[i].len != 0)
			rank[HuffCode[i].len]++;
		HuffCode[i].index = SortIndex[i];
	}

	for(i=0;i<=L;i++){
		codes[i+1] = (codes[i]+rank[i])<<1;
		rank[i] = 0;
	}

	//code
	for(i=0;i<Symbols;i++){
		HuffCode[i].code = codes[HuffCode[i].len] + rank[HuffCode[i].len]++;
	}
}
float BitsPerSymbol(HuffTable *HuffCode,int *weight,int Symbols,int WeightSum)
{
	float bitspersymbol = 0.0;
	int i;
	for(i=0;i<Symbols;i++){
		bitspersymbol += (float)HuffCode[i].len*weight[i];
	}
	return bitspersymbol/WeightSum;
}

//ascending order
void FreqSort(int *Freq,int *SortIndex,int Symbols)
{
	int i,j,tmp;
	for(i=0;i<Symbols;i++){
		for(j=i+1;j<Symbols;j++){
			if(Freq[i]>Freq[j]){
				tmp = Freq[i];
				Freq[i] = Freq[j];
				Freq[j] = tmp;

				tmp = SortIndex[i];
				SortIndex[i] = SortIndex[j];
				SortIndex[j] = tmp;
			}
		}
	}
}

//ascending order, quick sort
void QuickSort(int *arr, int *SortIndex,int startPos,int endPos)
{
	int i,j,key,index; 
	key=arr[startPos];
	index = SortIndex[startPos];
	i = startPos;	j = endPos; 
	while(i < j){
		while(arr[j]>=key && i<j)
			--j;
		arr[i]=arr[j];	SortIndex[i] = SortIndex[j];
		while(arr[i]<=key && i<j)
			++i; 
		arr[j]=arr[i];	SortIndex[j] = SortIndex[i];
	} 
	arr[i]=key;		SortIndex[i] = index;
	if(i-1 > startPos) 
		QuickSort(arr,SortIndex,startPos,i-1);
	if(endPos > i+1) 
		QuickSort(arr,SortIndex,i+1,endPos); 
}
int GenLenLimitedOptHuffCode(int *Freq,int Symbols)
{
	int i,j;
	unsigned char *Flag = NULL;		//record the state of the node
	unsigned int rank[MaxHuffLen];	
	Node *tree = NULL, *base = NULL, *left = NULL, *right = NULL;
	Node *start = NULL, *end = NULL, *Last = NULL;	//start:the first(min weight) node of 2*r,end:the last(max weight) node of 2*r,Last:the last node of array.
	Node *node = NULL;
	HuffTable HuffCode[MaxSymbols];
	float bitspersymbols = 0.0;
	int WeightSum = 0;
	int SortIndex[MaxSymbols];
	int X = (Symbols-1)<<MaxHuffLen;	//avoid float calculation
	int minwidth,r,weight;
	int r_Num = 0;
	
	if(Symbols > (1<<MaxHuffLen)){
		printf("Symbols > (1<<MaxHuffLen)\n");
		return -1;
	}

	for(i=0;i<MaxSymbols;i++){
		SortIndex[i] = i;
	}
	//FreqSort(Freq,SortIndex,Symbols);		//sort
	QuickSort(Freq,SortIndex,0,Symbols-1);		//sort

	for(i=0;i<Symbols;i++){	
		WeightSum += Freq[i];
	}
	tree = (Node *)malloc(Symbols*MaxHuffLen*2*sizeof(Node));
	memset(tree,0,Symbols*MaxHuffLen*2*sizeof(Node));		//2: for the optimize
	Flag = (unsigned char*)malloc(MaxHuffLen*Symbols*sizeof(unsigned char));
	memset(Flag,0x01,MaxHuffLen*Symbols*sizeof(unsigned char));	//mark every node 1
	memset(HuffCode,0,sizeof(HuffCode));

	for(i=0;i<MaxHuffLen;i++){
		for(j=0;j<Symbols;j++){
			tree[i*Symbols+j].depth = i;
			tree[i*Symbols+j].index = j;
			tree[i*Symbols+j].width = 1<<i;	//avoid float calculation
			tree[i*Symbols+j].weight = Freq[j];
		}
	}

	//start code
	base = tree;	Last = tree+MaxHuffLen*Symbols-1;
	while(X>0){
		minwidth = GetSmallestTerm(X);
		r = base->width;
		if(r > minwidth){	//there is no optimal solution.
			return -2;
		}	
		else if(r == minwidth){
			X -= minwidth;
			base++;
		}else{	//merge the smallest width and insert it into the original array
			if(r < (1<<(MaxHuffLen-1))){
				start = base+1;	r_Num = 1;
				//find start and end
				while(start->width < 2*r && start <= Last){
					r_Num++;
					start++;
				}
				end = start;
				while(end->width == 2*r && end <= Last){
					end++;
				}
				end--;
				//move back the (>=2*r)width node
				node = Last;	r_Num = r_Num/2;
				while(node >= start){
					*(node+r_Num) = *node;
					node--;
				}
				//package and merge
				node = start;
				start = start + r_Num;
				end = end + r_Num;
				for(i=0;i<r_Num;i++){
					left = base;	base++;
					right = base;	base++;
					weight = left->weight + right->weight;
					while(start <= end && start->weight <= weight){
						*node = *start;
						start++;
						node++;
					}
					node->weight = weight;	node->width = 2*r;
					node->left = left;		node->right = right;

					node++;
				}
				if(base->width == r){	//if r_Num is odd,remove the last r(width) Node.
					RemoveNodeMark(base,Flag,Symbols);
					base++;
				}
				Last += r_Num;
			}else{		//r >= (1<<(MaxHuffLen-1))
				while(base->width == r){
					left = base;	weight = base->weight;
					if((*(base+1)).width == r){
						base++;
						right = base;	weight += base->weight;
						base++;
						Last++;
						Last->weight = weight;	Last->width = 2*r;
						Last->left = left;		Last->right = right;
					}else{
						RemoveNodeMark(base,Flag,Symbols);
						base++;
					}
				}
			}
		} 
	}
	//output the HuffCode
	GenerateHuffmanCode(HuffCode,Flag,MaxHuffLen,Symbols,SortIndex);

	//print HuffCode
	for(i=0;i<Symbols;i++){
		printf("%03d weight:%04d Code:",HuffCode[i].index,Freq[i]);
		PrintHuffCode(HuffCode[i]);
		printf("\tCodeLen:%02d",HuffCode[i].len);
		printf("\n");
	}
	bitspersymbols = BitsPerSymbol(HuffCode,Freq,Symbols,WeightSum);
	printf("average code length:%f bits/symbol.\n",bitspersymbols);

	free(tree);	tree = NULL;
	free(Flag);	Flag = NULL;

	return 0;
}
#include <time.h>
int main()
{
// 	int Freq[MaxSymbols] = {1,25,3,4,9,6,4,6,26,15,234,4578};	//weight is not zero.
 	int Freq[MaxSymbols] = {10,6,2,1,1};	//weight is not zero.
 	GenLenLimitedOptHuffCode(Freq,5);		//5,12
 	return 0;
}

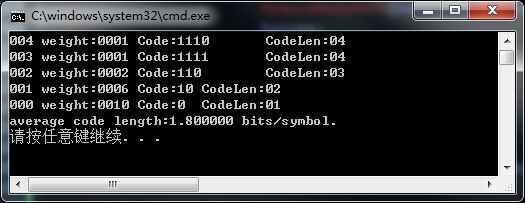
输出结果例如以下所看到的：