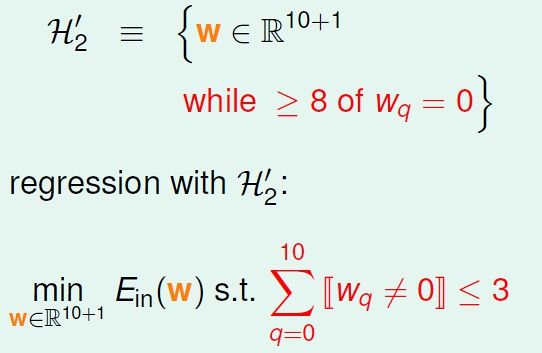NTU-Coursera机器学习:过拟合(Overfitting)与正规化(Regularization)
过拟合overfitting
过拟合(overfitting)定义
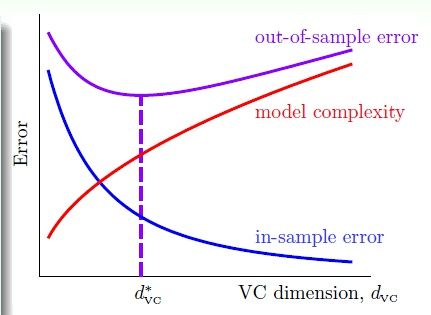
什么是过拟合(overfitting),即:简单的说就是这样一种学习现象:Ein 很小,Eout 却很大。而Ein 和 Eout 都很大的情况叫做 underfitting。这是机器学习中两种常见的问题。
上图中,竖直的虚线左侧是"underfitting", 左侧是"overfitting”。发生overfitting 的主要原因是:(1)使用过于复杂的模型(dvc 很大);(2)数据噪音;(3)有限的训练数据。
噪音与数据规模
我们可以理解地简单些:有噪音时,更复杂的模型会尽量去覆盖噪音点,即对数据过拟合!这样,即使训练误差Ein 很小(接近于零),由于没有描绘真实的数据趋势,Eout 反而会更大。即噪音严重误导了我们的假设。
还有一种情况,如果数据是由我们不知道的某个非常非常复杂的模型产生的,实际上有限的数据很难去“代表”这个复杂模型曲线。我们采用不恰当的假设去尽量拟合这些数据,效果一样会很差,因为部分数据对于我们不恰当的复杂假设就像是“噪音”,误导我们进行过拟合。
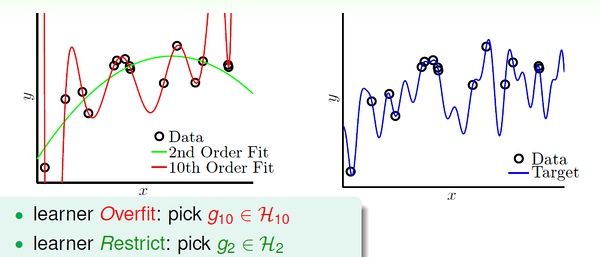
如下面的例子,假设数据是由50次幂的曲线产生的(下图右边),与其通过10次幂的假设曲线去拟合它们,还不如采用简单的2次幂曲线来描绘它的趋势。
随机噪音与确定性噪音 (Deterministic Noise)
之前说的噪音一般指随机噪音(stochastic noise),服从高斯分布;还有另一种“噪音”,就是前面提到的由未知的复杂函数f(X) 产生的数据,对于我们的假设也是噪音,这种是确定性噪音。
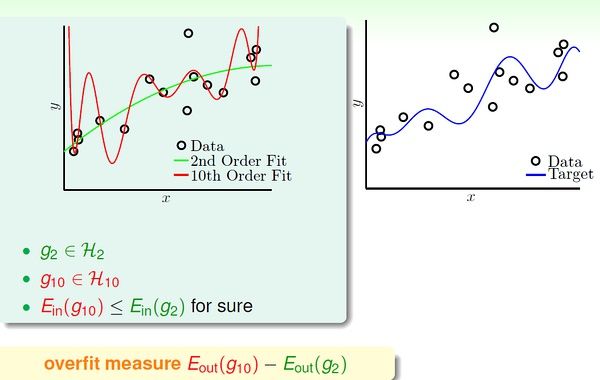
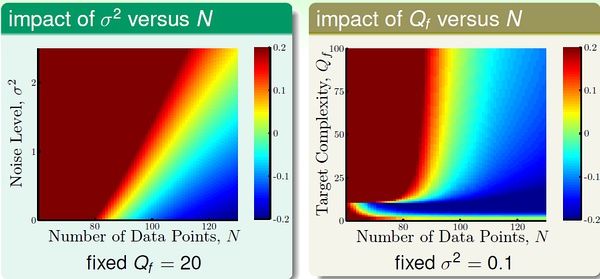
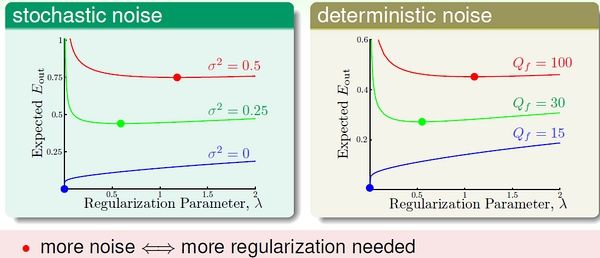
上图是关于2次曲线和10次曲线对数据的拟合情况,我们将overfit measure 表示为Eout(g10) - Eout(g2)。下图左右两边分别表示了随机噪音和确定性噪音对于Overfitting 的影响。
可见,数据规模一定时,随机噪音越大,或者确定性噪音越大(即目标函数越复杂),越容易发生overfitting。总之,容易导致overfitting 的因素是:数据过少;随机噪音过多;确定性噪音过多;假设过于复杂(excessive power)。
如果我们的假设空间不包含真正的目标函数f(X)(未知的),那么无论如何H 无法描述f(X) 的全部特征。这时就会发生确定性噪音。它与随机噪音是不同的。
我们可以类比的理解它:在计算机中随机数实际上是“伪随机数”,是通过某个复杂的伪随机数算法产生的,因为它对于一般的程序都是杂乱无章的,我们可以把伪随机数当做随机数来使用。确定性噪音的哲学思想与之类似。:-)
解决过拟合问题
对应导致过拟合发生的几种条件,我们可以想办法来避免过拟合。
- (1) 假设过于复杂(excessive dvc) => start from simple model
- (2) 随机噪音 => 数据清洗
- (3) 数据规模太小 => 收集更多数据,或根据某种规律“伪造”更多数据
正规化(regularization) 也是限制模型复杂度的。
- 数据清洗(data ckeaning/Pruning):将错误的label 纠正或者删除错误的数据。
- Data Hinting: “伪造”更多数据, add "virtual examples". 例如,在数字识别的学习中,将已有的数字通过平移、旋转等,变换出更多的数据。其他解决过拟合的方法在后面几讲介绍。
正规化-Regularization
正规化:Regularization
发生overfitting 的一个重要原因可能是假设过于复杂了,我们希望在假设上做出让步,用稍简单的模型来学习,避免overfitting。例如,原来的假设空间是10次曲线,很容易对数据过拟合;我们希望它变得简单些,比如w 向量只保持三个分量(其他分量为零)。
我们将此时的假设空间记为H(C),这是“正则化的假设空间”。
Weight Decay Regularization
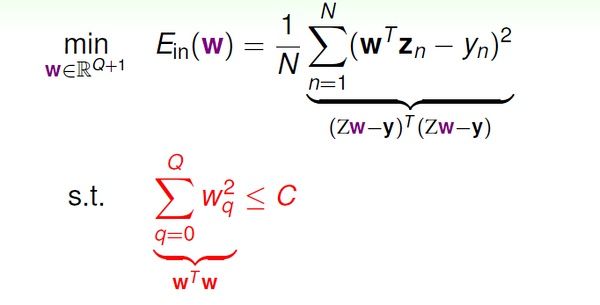
通过前面的分析,我们已经把优化问题变为:
接下来是通过一些几何解释,用lambda 替换常数C,便于优化问题的描述和求解。这个说起来很绕,就不多说了,以免误导各位。其实,这只是林轩田解释regularization 的一种方式,其他课程不一定从这个角度进行讲解的,这里模糊的话不必深究。个人觉得lambda 的表示方式本身就很直观了。 :-)
最后得到的优化目标是:
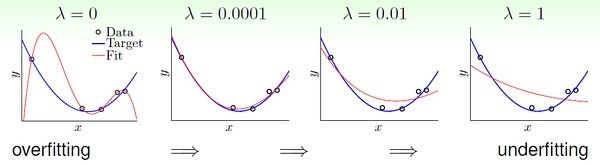
lambda 的大小对于拟合的影响,一个直观例子:
总之,lambda 越大,对应的常数C 越小,模型越倾向于选择更小的w 向量。
这种正规化成为 weight-decay regularization,它对于线性模型以及进行了非线性转换的线性假设都是有效的。
正规化与VC 理论
根据VC Bound 理论,Ein 与 Eout 的差距是模型的复杂度。也就是说,假设越复杂(dvc 越大),Eout 与 Ein 相差就越大,违背了我们学习的意愿。
对于某个复杂的假设空间H,dvc 可能很大;通过正规化,原假设空间变为正规化的假设空间H(C)。与H 相比,H(C) 是受正规化的“约束”的,因此实际上H(C) 没有H 那么大,也就是说H(C) 的VC维比原H 的VC维要小。因此,Eout 与 Ein 的差距变小。:-)
泛化的正规项 (General Regularizers)
指导我们更好地设计正规项的原则:target-dependent, plausible, friendly.
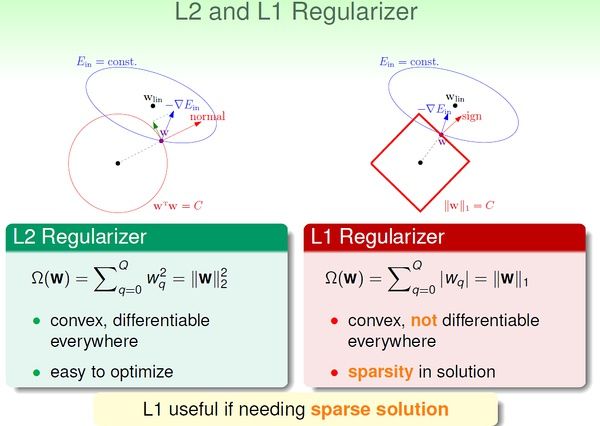
L2 and L1 Regularizer:
lambda 当然不是越大越好!选择合适的lambda 也很重要,它收到随机噪音和确定性噪音的影响。
关于Machine Learning更多讨论与交流,敬请关注本博客和新浪微博songzi_tea.