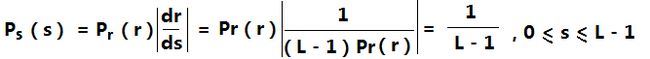【图像处理笔记】直方图均衡
直方图均衡。 histogram equalization。
考虑连续灰度值,并用变量r表示待处理图像的灰度。通常,我们假设r的取值区间为[0,L - 1],r = 0表示黑色,r = L - 1表示白色。
![]()
对于上式,我们假设:
(a)T(r)在区间上为单调递增函数。
(b)当0 <= r <= L - 1时,0 <= T(r) <= L - 1
在后面讨论的一些公式中,我们会用到T(r)的反函数
在这种情况下,条件(a)改为(a‘)T(a)在区间上为严格单调递增函数。
条件(a)中要求T(r)为单调递增函数,是为了保证输出的灰度值不少于相应的输入值,防止灰度反变换时产生人为的缺陷。
条件(a’)特意强调严格单调递增,是为了保证从S到 r 的反映射是一对一的,防止二义性。
因为在实践中,我们处理的数字图像,都是整数的灰度值,必须把所有的结果四舍五入为最接近的整数值,所以一对一的映射无法满足。
因此,当严格单调不满足时,我们就要使用寻找最接近整数匹配的方法来解决非唯一反变换的问题。
一幅图像的灰度级可以看成是[0,L - 1]内的随意变量。随机变量的基本描绘子是其概率密度函数(PDF)。
令Pr(r)和Ps(s)分别表示随机变量r 和s 的PDF。由基本概率论得到的一个基本的结果是,如果Pr(r)和T(r)已知,且在感兴趣的值域上T(r)是连续且可微的,则映射后的PDF可表示为:
可知,S的PDF是由输入灰度的PDF和变换函数决定的。
在图像处理中,有一个特别重要的变换函数有如下的形式:
其中,w 是积分的假变量。
公式右边是随机变量r 的累计分布函数(CDF)。
由基本积分学中的莱布尼兹准则知道,关于上限的定积分的导数是被积函数在该上限的值。
可得到如下推导:
根据推导可知,Ps(s)是一个均匀概率密度函数。
简而言之,我们已经证明了,执行s = T(r)的灰度变换将得到一个随机变量s ,该随机变量由一个均匀PDF表征。
下图说明了以上结论~
对于离散的数值,我们处理其概率(直方图值)与求和来替代处理概率密度函数与积分。
一幅数字图像中,灰度级rk 出现的概率近似为:
nk是灰度为rk的像素的个数。
与rk相对应的Pr(rk)图形,通常称为直方图。
上式将输入图像中灰度级为rk的各像素,映射到输出图像中灰度级为Sk的对应像素得到。
变换T(rk)称为直方图均衡或直方图线性变换。
因为直方图是PDF的近似,而且在处理中不允许造成新的灰度级,所以在实际的直方图应用中很少见到完美平坦的直方图。因此,与连续的情况不同,通常不能证明离散直方图均衡会导致均匀的直方图。
直方图均衡化,具有展开输入图像直方图的趋势,均衡后的图像的灰度级跨越更宽的灰度级范围。所以最终得到的结果是增强了对比度。
公式的推导较为晦涩难懂,但是直方图均衡化的物理意义还是较为明确的。
总体思想就是,把原来灰度图中,较为集中的灰度区间,映射到全部范围内的均匀分布。重新分配图像的像素值。从而增强了图像的对比度。
这种方法对于背景和前景都很亮或者很暗的图像有较好的效果。
以下是用VB.NET来实现的直方图均衡化:
'直方图均衡化
'首先应该求出图像的灰度分布
Dim img As New Image(Of Gray, Byte)("C:\test1.bmp")
Dim height As Integer = img.Height
Dim width As Integer = img.Width
'统计每级灰度的像素个数
Dim pixelCounts(255) As Integer
For i = 0 To height - 1
For j = 0 To width - 1
pixelCounts(img.Data(i, j, 0)) = pixelCounts(img.Data(i, j, 0)) + 1
Next
Next
'统计每级灰度的累计像素个数
Dim pixelAccumulative(255) As Integer
For i = 0 To 255
For j = 0 To i
pixelAccumulative(i) = pixelAccumulative(i) + pixelCounts(j)
Next
Next
'根据像素的灰度值映射到新的灰度值
For i = 0 To height - 1
For j = 0 To width - 1
img.Data(i, j, 0) = (256 - 1) / (width * height) * pixelAccumulative(img.Data(i, j, 0))
Next
Next
img.Save("C:\直方图均衡化\test1.bmp")


可以看到,直方图均衡化后,图片的对比度增加了。
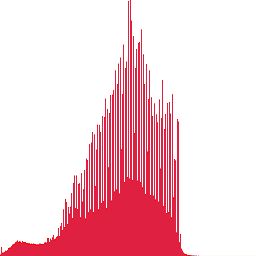
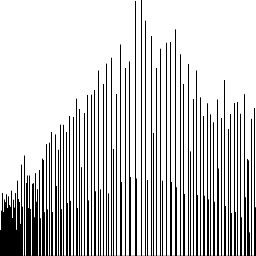
再来看看变换前和变换后的直方图。
图像的直方图也被扩展到了几乎所有的灰度级。